Методичні вказівки до курсової роботи з дисципліни Інформатика, Розв'язання задач матричної алгебри
« Назад
ВступДана курсова робота виконується для закріплення знань з курсу «Основи інформаційних технологій і програмування». Змістом курсової роботи передбачено: - математичне формулювання задачі – побудова математичної моделі задачі й опис зв’язку між об’єктами задачі; - розробка алгоритму рзв’язання задачі; - програмування задачі; - налаштування програми, у тому числі візуальний і синтаксичний контроль; - рзв’язання задачі й одержання результатів. Методичні вказівки складаються з трьох розділів. У першому розділі описано роботу з одновимірними і двовимірними масивами, наведенні приклади обробки масивів. Другий розділ – робота з матрицями: опис матриць, їхні види й операції над матрицями. У третьому –подано варіанти завдань. До захисту подають розрахунково – пояснювальну записку. 1. Масиви1.1. Опис та ініціалізація масивівМасив – це звичайно іменована послідовність однотипних величин. Масиви можуть бути будь-якого типу: цілі, дійсні, символьні. Опис масиву в програмі, написаної на С, відрізняється від опису простої змінної наявністю після імені масиву квадратних дужок [], у яких задається кількість елементів масиву (розмірність). Для оголошення простого одновимірного масиву використовується така форма: тип ім'я [розмір]; тип – тип даного кожний з елементів масиву, ім’я – ім’я масиву, розмір – кількість елементів масиву. Наприклад: float A [5];опис масиву А, що складається з 5 дійсних чисел. int N[22]; опис масиву N, що складається з 22 цілих чисел. У випадку багатовимірних масивів розмір визначається кількістю пар дужок, а число усередині дужок показує розмір масиву у даному вимірі. Наприклад, опис двовимірного масиву виглядає так: double mass [5][12];опис масиву mass, має 5 елементів, кожен з яких є масивом, що складається з 12 значень типу double. Такий опис можна трактувати як матрицю, що складається з 5 рядків і 12 стовпців. У пам’яті машини такий масив розташовується послідовно рядками. Для звертання до деякого елемента масиву зазначають його ім’я й індекс, узятий у квадратні дужки. Для двовимірного масиву – індекс рядка вказується у першій дужці, а індекс стовпця - у других. Як індекс можна вживати вираз цілого типу – константу або змінну. Індекс може змінюватися від 0 до n - 1, де n – кількість елементів. Доступ до елемента масиву можна здійснити за допомогою покажчика. Індекси масиву в мові С завжди починаються з 0, а не з 1. Наприклад, опис одновимірного масиву float A[5]; складеного з елементів А[0], A[1], A[2], A[3],A[4] (А[2] – звертання до третього елемента масиву А). Для двовимірного: double mass [5][12]; складеного з елементів mass[0][0], mass[0][1], mass[0][2]………mass[4][11]; (mass[0][4] звертання до п’ятого елемента масиву mass). При описі масиву використовуються ті ж самі модифікатори (класи пам’яті, константи та ініціалізатори), що і для простих змінних. Ініціалізуюче значення для масивів записують у фігурних дужках. Значення елементам надаються один за одним. Якщо елементів у масиві більше, ніж ініціалізаторів, тоді елементи, для яких значення не зазначені, дорівнюють нулю: float A[5] = {3.2, 5.1, 4.2}; тобто A[0]=3.2, A[1]=5.1, A[2]=4.2, A[3]=0, A[4]=0 Багатовимірний масив при ініціалізації можна подати як масив з масивів, при цьому кожен масив береться у свої фігурні дужки (у цьому випадку ліву розмірність можна не вказувати), або задається загальний список елементів у тому порядку, в якому елементи розташовуються в пам’яті: int mass [ ][2] = { {1, 1}, {0, 2}, {1, 0} }; або int mass [3][2]={ 1, 1, 0, 2, 1, 0 }; Розмірність масиву разом з типом його елементів визначає обсяг пам'яті, необхідний для розміщення масиву, що виконується на етапі компіляції, тому розмірність може бути задана тільки цілою додатною константою або константним виразом. Якщо при описі масиву не зазначена розмірність, тоді обов’язково має бути ініціалізатор; у цьому випадку компілятор виділить пам'ять відповідно до кількості ініціалізуючих значень. 1.2. Введення/виведення масивівДля введення/виведення масивів зручно використовувати оператор циклу for: for(вираз 1; вираз 2; вира 3) Вираз 1 – ініціалізація (початкове значення індексу масиву), виконуєтьсяодин раз, коли починає виконуватися цикл. Вираз 2 – перевірка умови закінчення циклу (значення або вираз, яким характеризується кінцевий індекс масиву), обчислюється перед кожним можливим виконанням циклу. Вираз 3 – коригувальний вираз, у якому виконується зміна або відновлення виразу, обчислюється наприкінці кожної ітерації. Введення одновимірного масиву цілих чисел з клавіатури: for (i=0; i<10; i++) scanf(“%d”,&A[i]); Введення двовимірного масиву цілих чисел з клавіатури: for (i=0; i<10; i++) for (j=0; j<10; j++) scanf(“%d”,&B[i][j]); Оскільки зміна j- го індексу відбувається швидше, ніж i-го, то вводиться двовимірний масив рядками. Виведення одновимірного масиву цілих чисел на екран: for (i=0; i<10; i++) printf(“%d”,A[i]); Виведеня двовимірного масиву цілих чисел на екран рядками: for (i=0; i<10; i++) { for (j=0; j<10; j++) printf(“%d”,B[i][j]); printf(“\n”); } Для файлового введення/виведення масиву застосовують відповідні функції: fscanf(), fprintf() розміщені в циклі. Функції fscanf(), fprintf() працюють також, як scanf(), printf(), з тією лише різницею, що перший аргумент – покажчик на файл. Наприклад: for (i=0; i<10; i++) fscanf(ou,“%d”,&A[i]); де ou покажчик на файл, відкритий для читання даних; for (i=0; i<10; i++) fprintf(ot,“%d”,A[i]); де ot покажчик на файл, відкритий для запису даних. Приклад 1. Підрахунок суми елементів одновимірного масиву: # include <stdio.h> #define n 10//розмір масиву int main () { int i , sum = 0;// ініціалізація змінної sum int mass [n] = {3, 4, 5, 4, 4, 6, 1, 7, 8, 5}; //ініціалізація масиву цілих чисел for (і=0; і<n; і++) sum +=mass[i]; //визначення суми елементів масиву printf(“Сума елементів: %5d”,sum); return 0; } При оголошенні кількості елементів масиву зручно використовувати іменовану константу, оголошену в директиві #define. Оскільки при такому підході для її зміни достатньо скорегувати значення константи усього лише в одному місці програми. Приклад 2. Обчислення суми елементів двовимірного масиву за стовпцями: # include <stdio.h> # include <conio.h> #define R 3//кількість рядків #define C 5//кількість стовпців int main () { int a[R][C]; //опис масиву цілих чисел int s[C]//сума елементів у стовпцях int і,j; printf (“Уведіть масив\n”); printf (“Після введення елементів кожного рядка ,\n”); printf (“%d цілих чисел, натискайте <Enter>\n”,C); for(i=0; i<R; i++) { printf(“->”); for (j=0; j<C; j++) scanf(“%d”,&a[i][j]); } printf(“\nвведен масив\n”); for(i=0; i<R; i++) { printf(“->”); for (j=0; j<C; j++) printf(“ %d ”, a[i][j]); printf(“\n”); } //“очистимо масив s” for(i=0; i<R; i++) s[i]=0; //обробка for (j=0; j<C; j++)//для кожного стовпця підсумовуємо елементи for(i=0; i<R; i++) s[j]+=a[i][j]; printf(“---------------------------------------------”); for(i=0; i<C; i++) printf(“%d ”,s[i]); printf(“Для завершення натисніть <Enter>”); getch(); return 0; } 1.3. Масиви, як аргументи функціїВикористовуючи масив як аргумент функції, у цю функцію передається покажчик на його перший елемент, іншими словами, передається за адресою. У мові С ім’я масиву, одновимірного або двовимірного, є покажчиком на перший елемент масиву. При цьому інформація про кількість елементів масиву втрачається, і тому доцільно передавати його розмірність через окремий параметр. Якщо розмірність масиву є константою, то можна навести її при описі формального параметра і як межі циклів при обробці масиву усередині функції. Усередині функції масив інтерпретується як одновимірний, а його індекс зазначається в програмі. Розглянемо одномірний масив int A[5] і двовимірний масив int B[5][5]. Одновимірні і двовимірні масиви, що використовуються у функціях-підпрограмах, повинні бути передані у функцію за певними правилами, а саме: Опис функції або створення прототипу функції. Звичайно описується функція в головній програмі перед описом змінних. Так само її можна описати в заголовку функції main(). У дужках зазначають формальні параметри і їх тип. Якщо формальним параметром є масив, то записують покажчик на перший елемент масиву. Перед ім’ям функції-підпрограми наводять тип функції, у нашому випадку – int. Тип функції визначається типом значення, яке повертається з функції-підпрограми в головну функцію. Опис функції в основній програмі int func1 (int А1[]); або int func1 (int *А1); int func2 (int А2[][5]); або int func2 (int (*А2)[5]); Виклик функції в основній програмі. У головній функції викликається функція із зазначенням імен і списку фактичних параметрів: func1(A); func2(В); При виклику у функцію передається ім’я фактичного масиву (адреси першого елемента), тобто того масиву, що використовується в основній програмі. Визначення функції. Після головної функції створюють функцію- підпрограмму, причому в тому самому порядку, що і функцію main(): int func1 (int А1[]) { Тіло функції; } int func2 (int А2[][5]) { Тіло функції; } Приклад 3. Дано дві матриці розмірністю [3х4]. Знайти суму матриць. Оформити розв’язання основної задачі у вигляді функції-підпрограми. #include <stdio.h> #include <graph.h> #define M 3 #define N 4 //опис функції-підпрограми, у дужках записуємо покажчик на перший //елемент масиву. int slogenie (int T[][M],int K[][M],int s,int F[][M]); int main (void) { int A[M][N],B[M][N],C[M][N]; int i,j; _clearscreen(_GCLEARSCREEN); printf("Вводимо матрицю A[3][4]\n"); for(i=0;i<M;i++) for(j=0;j<N;j++) scanf("%d",&A[i][j]); printf("Вводимо матрицю B[3][4]\n"); for(i=0;i<M;i++) for(j=0;j<N;j++) scanf("%d",&B[i][j]); printf("Матриця суми: C[3][4]\n\n"); slogenie (A,B,4,C); //виклик функції-підпрограми в дужках //указуємо фактичні параметри for(i=0;i<M;i++) { for(j=0;j<N;j++) printf("%5d",C[i][j]); putchar('\n'); } } /* **************************************************** */ //визначення функції – підпрограми int slogenie (int (*T)[M],int K[][M],int s,int F[][M]) { int i,j; for(i=0;i<s;i++) for(j=0;j<M;j++) F[i][j]=T[i][j]+K[i][j]; } 2. Матриці2.1. Види матрицьМатриця – двовимірний масив чисел вигляду: Матриця характеризується розмірністюm ´ n, тобто добутком числа рядків m на число стовпців n. Квадратна матриця має m = n і розмірність n2 = n ´ n. Діагональна матриця є різновидом квадратної матриці вигляду: У ней усі елементи нульові, крім діагональних, тобто A[i][j] ¹ 0 при i = j. Одинична матриця – різновид діагональної матриці, у якої поточний елемент A[i][j] = 1 при i = j. Транспонованою матрицею АТ називається квадратна матриця, у якої стовпці відповідають рядкам квадратної матриці А. Діагональні елементи в матриці А і АТ, однакові й операція транспонування зводиться до перестановки інших елементів симетрично щодо діагоналі. Це реалізується за допомогою співвідношення aTij =aij при i ≠ j: 2.2. Операції з матрицямиОперації з константами. Операції з константами зводяться до додавання або віднімання кожного елемента матриці з константою: С[i][j]= A[i][j] ± X, або множення C[i][j]=A[i][j] * X чи ділення C[i][j]=A[i][j] / X на константу. Додавання і віднімання для двох матриць А і В з однаковою розмірністю m = n виконується за формулою: cij = aij ± bij , де i = 1,2,…,m та j = 1,2,…,n…. Тут сij – елементи результуючої матриці С. Множення матриці А з розмірністю m = n і В з розмірністю n ´ l (число стовпців матриці А дорівнює числу рядків матриці В) виконується за формулою: де j = 1,2,…,l та k=1,2,…,m…. Отримана матриця С має розмірність m´ l.
Множення матриці А з розмірністю m ´ n на вектор R з розмірністю n (число стовпців матриці А дорівнює числу рядків R) здійснюється за формулою: де i=1,2,…,m. Одержуваний вектор U має розмірність m . Приклад 4: А[4][5] ´ R[5] = U [4] (тобто m = 4, n = 5): Визначником матриці D розміром 2´2 називається число, що позначається символом Визначником матриці D розміром 3´3 називається число, що позначається символом Визначник матриці D розміром 4´4 визначається за формулою: Приклад 5: Сідлова точка матриці. Матриця А має сідлову точку Аij, якщо Aij є мінімальним елементом у i-оу рядку і максимальним у j-му стовпці. Приклад 6: Дана матриця А[3][3] та В[3][3]. Знайти сідлові точки матриць. А11=5 – це сідлова точка матриці А. Матриця В сідлова точку не має. Операція згладжування матриці. Операція згладжування матриці дає нову матрицю того ж розміру, кожен елемент якої виходить як середнє арифметичне наявних сусідів відповідного елемента початкової матриці. Сусідами елемента Аij у матриці А назвемо елементи Akl з ( і - 1 ≤ k ≤ 0 i + 1 ), ( j - 1 ≤ l ≤ j + 1 ), ( k , l ) ≠ ( i , j ). Приклад 7: Дана матриця А[6][5]. Побудувати результат згладжування заданої матриці А.
Елемент отримаємо, як І так далі.
3. Варіанти завдань до курсової роботи
Список літератури1. Павловская Т. А. С/С++ Програмирование на языке високого уровня. – СПб.: Питер, 2004. 2. Прата С., Язык програмирования С. – К: DiaSoft, 2000. 3. Краткий конспект лекций по курсу «Пользыватель ПЭВМ» для слушателей системи повышения квалификации / Сост.: О. Г. Кравец, Е. В. Лусиф и др. - Х: МИПК-ХГПУ, 1998. З повагою ІЦ "KURSOVIKS"! |
,
,
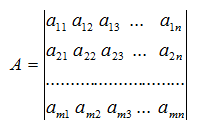
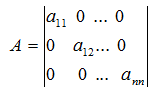
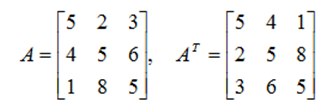
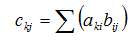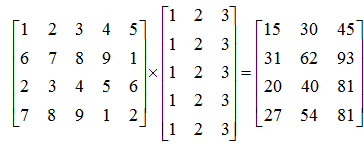
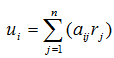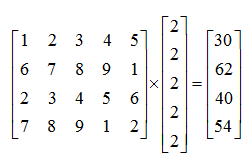
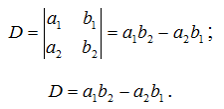
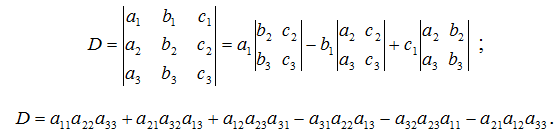
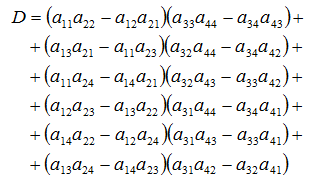
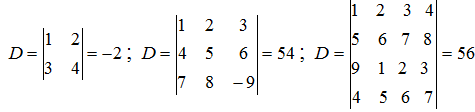
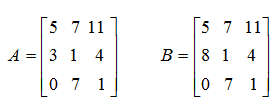
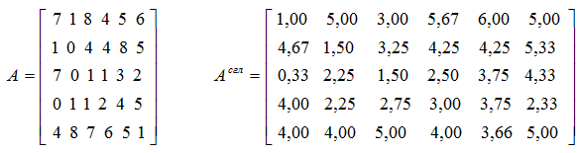
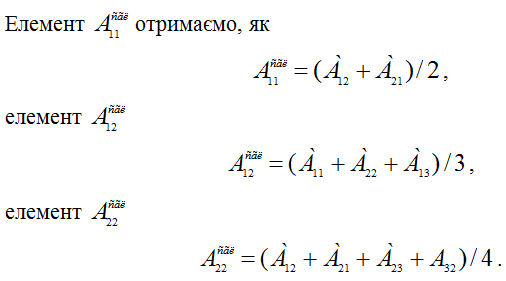
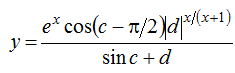при х = 0,5, с = 0,5, d = 0,75. Помножити вихідну матрицю на значення y. Визначити: кількість рядків, що не містять жодного нульового елемента; максимальне з чисел, що зустрічаються в даній матриці більше одного разу.
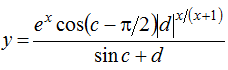при х = 0,5, с = 0,5, d = 0,75. Помножити отриману матрицю на значення y.
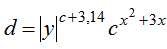, де у = –4,45, с = 0,52, х = 0,44. Визначити кількість стовпців, що містять хоча б один нульовий елемент; номер рядка, у якому міститься найдовша серія однакових елементів.
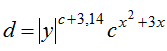, де у = –4,45, с = 0,52, х = 0.44. Визначити добуток елементів у тих стовпцях, що не містять від’ємних елементів. Мінімум серед сум модулів елементів діагоналей, рівнобіжних побічній діагоналі матриці.
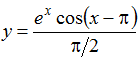, де х = 0,05.
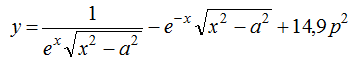, де х = 1,5, а = 4, р = 1,6. Порахувати кількість локальних мінімумів отриманої матриці. Елемент матриці називається локальним мінімумом, якщо він строго менше ніж всі наявні у нього сусіди. Знайти суму модулів елементів, розташованих вище головної діагоналі.
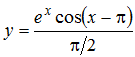, де х =0 ,05. Визначити кількість від’ємних елементів у тих рядках, що містять хоча б один нульовий елемент.
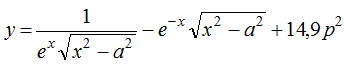, де х = 1,5, а = 4, р = 1,6. Визначити: кількість рядків, що не містять нульових елементів; мінімальне з чисел, які зустрічаються в даній матриці більше одного разу.
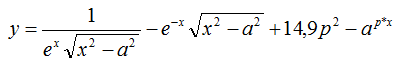, де х = 2,1, а = 4,5, р = 1,6 Обчислити визначник результуючої матриці. Відсортувати стовпці матриці по зростанню. Знайти суму модулів елементів, розташованих вище головної діагоналі.
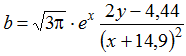, де х = 4,5. Порахувати визначник результуючої матриці. Відсортувати рядки матриці за зростанням. Знайти суму модулів елементів, розташованих під побічною діагоналлю.
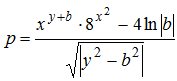, де х = 0,54, у = 4,87, b = 4. Визначити кількість від’ємних елементів у тих рядках, що містять хоча б один нульовий елемент.
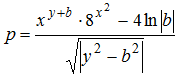, де х = 0,54, у = 4,87, b = 4. Визначити в отриманій матриці суму елементів у тих рядках, що не містять від’ємних елементів, суму елементів головної діагоналі.
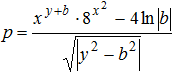, х = 0,54, у = 4,87, b = 0,5.
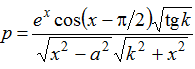, х = 0,54, k = 0,05. Визначити номери рядків і стовпців усіх сідлових точок (матриця А має сідлову точку Аij , якщо Aij є мінімальним елементом в i-му рядку і максимальним в j-му стовпці).