Лабораторна робота №2 з курсу HCI на тему Швидкісна і просторова оцінка інтерфейсу

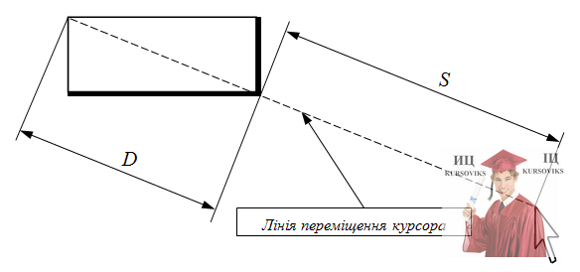
ЗМІСТ

ЛАБОРАТОРНА РОБОТА № 2. ШВИДКІСНА І ПРОСТОРОВА ОЦІНКА ІНТЕРФЕЙСУ   3

Завдання до роботи. 3

Зміст звіту. 3

Контрольні запитання. 3

Варіанти завдань на лабораторну роботу: 4

Основні теоретичні відомості 4

1. Модель GOMS для проведення порівняльної оцінки інтерфейсів користувача  4

2. Операції, що входять в модель GOMS. 4

3. Правила розстановки ментальних операцій. 5

4. Закон Фітса. 7

5. Закон Хіка. 8

ЛАБОРАТОРНА РОБОТА № 2. ШВИДКІСНА І ПРОСТОРОВА ОЦІНКА ІНТЕРФЕЙСУ

Мета роботи: Дослідити кількісні методи аналізу інтерфейсу і отримати практичні навички оцінювання швидкості інтерфейсу за моделлю GOMS, законами Фітца і Хіка.

Завдання до роботи

1. Обрати та узгодити з викладачем об'єкт для проектування.

2. Розрахувати по моделі GOMS час виконання дій для функцій, розроблених в лабораторній роботі 1.

3. Розрахувати по закону Фітца час виконання дій для функцій, розроблених в лабораторній роботі 1.

4. Розрахувати значення згідно з законом Хіка для функцій з лабораторної роботи 1.

5. Оформити звіт по роботі.

6. Відповісти на контрольні питання.

Зміст звіту

1. Тема та мета роботи.

2. Завдання до роботи.

3. Аналіз дій інтерфейсу функцій, що проектується.

4. Результати застосування методики GOMS та законів Фітца і Хіка.

4. Висновки, за результатами виконання роботи.

Контрольні запитання

1. Склад операцій моделі GOMS

2. Правила розстановки ментальних операцій GOMS

3. Сформулюйте закон Фітца.

4. Сформулюйте закон Хіка.

Варіанти завдань на лабораторну роботу:

1. Бронювання місць у театр;

2. Переклад чисел з однієї системи в іншу;

3. Запис на прийом до зубного лікаря;

4. Керування кухонними приладами;

5. Керування засобами пересування (скутер, літаюча тарілка, …);

6. Підбор гармонійних кольорових схем;

7. Навчальна система "Столиці держав";

8. Створення фоторобота;

9. АРМ медсестри в лікарняному відділенні;

10. Підбір варіантів для студії з дизайну штор;

11. Навчальна система "Англійська мова для малюків";

12. Ознайомлення з прогнозом погоди;

13. Перевірка знань з географії, сольфеджіо, хімії.

14. Ваша власна тема.

Основні теоретичні відомості

1. Модель GOMS для проведення порівняльної оцінки інтерфейсів користувача

GOMS (the model of goals, objects, methods, and selection rules). Модель, заснована на оцінці швидкості друку. Розробники моделі GOMS у час її створення помітили, що час, потрібний для виконання якогось завдання системою «користувач-комп'ютер», є сумою всіх тимчасових інтервалів, які потрібні були системі на виконання послідовності елементарних жестів, що складають дану задачу.

2. Операції, що входять в модель GOMS

K = 0.2 с. Натискання клавіші. Час, необхідний для того, щоб натиснути клавішу.

P = 1.1 c. Вказівка. Час, необхідний для того, щоб вказати на якусь позицію на екрані монітора.

H = 0.4 с. Переміщення. Час, необхідний користувачу для того, щоб перемістити руку з клавіатури на ГПВ (графічний пристрій введення) або з ГПВ на клавіатуру.

М = 1.35 с. Ментальна підготовка. Час, необхідний користувачу для того, щоб розумово підготуватися до наступного кроку.

R. Відповідь. Час, протягом якого користувач повинен очікувати відповідь комп'ютера.

3. Правила розстановки ментальних операцій

Правило 0. Початкова розстановка оператора М: Оператори М слід встановлювати перед усіма операторами К (натискання клавіші), а також перед усіма операторами P (вказівка за допомогою ГПВ), призначеними для вибору команд; але перед операторами P, призначеними для вказівки на аргументи цих команд, ставити оператор М не треба.

Правило 1. Видалення очікуваних операторів М: Якщо оператор, наступний за оператором М, є повністю очікуваним з точки зору оператора, попереднього М, то цей оператор М може бути видалений.

Наприклад, якщо ви переміщаєте ГПВ з наміром натиснути його кнопку після досягнення мети руху, то відповідно до цього правила слід видалити оператор М, встановлюваний за правилом 0. У цьому випадку послідовність P M K перетворюється в P K.

Правило 2. Видалення операторів М всередині когнітивних одиниць: Якщо рядок виду М К М К М К... Належить когнітивній одиниці, то слід видалити всі оператори М, крім першого. Когнітивної одиницею є безперервна послідовність символів, що вводять, які можуть утворювати назву команди або аргумент. Наприклад «Y», «переміщати», «4,556» є прикладами когнітивних одиниць.

Правило 3. Видалення операторів М перед послідовними роздільниками: Якщо оператор К означає зайвий розділовий знак, який стоїть в кінці когнітивної одиниці (наприклад, роздільник команди, наступної відразу за роздільником аргументу цієї команди), то слід видалити оператор М, що стоїть перед ним.

Правило 4. Видалення операторів М, які є переривниками команд: Якщо оператор К є роздільником, що стоять після постійної рядки (Наприклад, назва команди або будь-яка послідовність символів, яка кожен раз вводиться в незмінному вигляді), то слід видалити оператор М, що стоїть перед ним. (Додавання роздільника стане звичним дією, і тому роздільник стане частиною рядка і не буде вимагати спеціального оператора М.) Але якщо оператор До є роздільником для рядка аргументів або будь-який інший змінною рядки, то оператор М слід зберегти перед ним.

Правило 5. Видалення перекривають операторів М: Будь-яку частину оператора М, яка перекриває оператор R, що означає затримку, пов'язану з очікуванням відповіді комп'ютера, враховувати не слід.

Розглянемо конкретний приклад розрахунку часу за допомогою моделі GOMS:

Для початку складемо послідовність дій, які виконуються в даному вікні інтерфейсу. Вона буде включати в себе вибір компанії і терміналу. потім натискання кнопки «Далі».

1. Отримаємо послідовність: PKPKPKPKPK.

2. Далі за правилом 0 ставимо перед кожними P і K, операцію М:

MPMKMPMKMPMKMPMKMPMK.

3. За правилом 1, PMK переходить в PK: MPKMPKMPKMPKMPK.

4. Останні дві операції P і K, припускають вибір і натискання кнопки «Далі». Так як це цілком очікуване дію, то останню М ми також прибираємо. Після чого в підсумку отримаємо: MPKMPKMPKMPKPK.

5. Так як інші правила не застосовуються, то взявши дані нам значення часу виконання операцій, отримаємо Т = 11.8 сек.

4. Закон Фітса

В 1954 році Поль Фітс (Paul Fitts) сформулював правило, яке пізніше стало відомим як закон Фітса: час досягнення цілі обернено пропорційний її розміру і прямо пропорційний дистанції до неї.

Різні когнітивні закони, які мають відношення до розробки інтерфейсів (в тому числі і закон Фітса), дають додаткові дані, на основі яких можна приймати ті або інші рішення, які пов’язані з розробкою інтерфейсів. Закон Фітса дозволяє кількісно визначити те, що чим далі знаходиться об’єкт від поточної позиції курсора або чим менше розміри цього об’єкта, тим більше часу потрібно користувачу для переміщення до нього вказівника миші (курсора).

Припустимо, що ви переміщуєте курсор до кнопки, яка зображена на екрані, і яка є метою даного переміщення. В законі Фітса дистанція визначається як довжина прямої лінії, яка з’єднує початкову позицію курсора і найближчу точку цільового об’єкта, а розмір об’єкта визначається уздовж лінії переміщення курсора (рис. 1).

Рис. 1 - Схема вибору об’єкта

В одновимірному випадку час досягнення об’єкта по закону Фітса визначається наступним чином:

t = a + b log2 (S/D+1),

де t – час (мс); S – дистанція від курсора до об’єкта; D – розмір об’єкта вздовж лінії руху курсора; a, b – константи, які встановлюються досвідченим шляхом по параметрам продуктивності користувача (для наближених обчислень використовують a = 50, b = 150).

Час, який обчислюється, відраховується від моменту, коли курсор починає рух по прямій лінії, до моменту, коли користувач клацає мишкою по цільовому об’єкту. Логарифм по основі 2 є мірою труднощі задачі в кількості біт інформації, яке потребує для опису (одномірного) шляху переміщення курсора.

Для обчислення часу можна використовувати будь-які одиниці виміру дистанції, так як S/D є відношенням двох дистанцій і тому не залежить від одиниці виміру. Звідси випливає, що хоча вказівний пристрій може переміститись на відстань більшу або меншу, чим та відстань, на яку переміститься на екрані курсор, закон все одно буде працювати при умові, що співвідношення між рухом мишки і курсора є лінійним. Закон Фітса може застосовуватись тільки до тих типів переміщень, які здійснюються при використанні більшості людино-машинних інтерфейсів, тобто до таких переміщень, які невеликі відносно розмірів людського тіла і які є неперервними (здійснюються одним рухом).

5. Закон Хіка

Перед тим як перемістити курсор до мети або зробити будь-яке інше дію з набору множини варіантів, користувач повинен вибрати цей об'єкт або дію. У законі Хіка стверджується, що коли необхідно зробити вибір з n варіантів, час на вибір одного з них буде пропорційний логарифму за основою 2 від числа варіантів плюс 1, за умови, що всі варіанти є рівно імовірними. У цьому виді закон Хіка дуже схожий на закон Фітса:

ТХ = a + b log2 (n + 1)

Якщо ймовірність 1-го варіанту дорівнює p (i), то замість логарифмічного коефіцієнта використовується

Σ (p (i) log2 (1 / p (i) +1))

Коефіцієнти, що використовуються в вираженні закону Хіка, у великій мірі залежать від багатьох умов, включаючи те, як представлені можливі варіанти, і те, наскільки добре користувач знайомий з системою. (Зауваження. Якщо варіанти представлені незрозумілим чином, значення a і b зростають. Наявність навичок і звичок у використанні системи знижує значення b.) Ми не будемо розглядати ці залежності - для нас важливо, що для прийняття того чи іншого рішення потрібен час; що для прийняття складних рішень потрібно більше часу, ніж для прийняття простих рішень; і що взаємозв'язок є логарифмічним. При відсутності більш точних даних для проведення швидких і приблизних обчислень ми можемо скористатися тими ж значеннями a і b, які використовували для закону Фітса.

При використанні будь-яких позитивних і ненульових значень a і b з закону Хіка випливає, що надання користувачу відразу декількох варіантів одночасно зазвичай є більш ефективним, ніж організація тих же варіантів в ієрархічні групи. Вибір з одного меню, що складається з 8 елементів, робиться швидше, ніж з двох меню, що складаються з 4 елементів кожне. Якщо всі елементи можуть бути обрані з однаковою ймовірністю, і якщо не враховувати час, необхідний для відкриття другого меню, то порівняння часу для вибору одного елемента з восьми (a + b log2 8) з подвоєним часом для вибору одного елемента з чотирьох 2 (a + b log2 4) покаже, що:

а + 3b <2 (а + 2b)

оскільки log₂ 8 = 3, a log₂ 4 = 2, а також, оскільки a <2a і 3b <4b.

Це узгоджується з даними, отриманими в експериментах зі структурами меню.

Даний розгляд законів Фітса і Хіка не можна вважати повним. Проте, цього короткого розгляду цілком достатньо для того, щоб відзначити їх цінність з точки зору розробки інтерфейсів. Вони можуть бути корисними навіть в тому випадку, коли емпіричні значення коефіцієнтів a і b не відомі (як це було в нашому прикладі).

З повагою ІЦ "KURSOVIKS"!