Лабораторна робота №1 на тему Розробка і реалізація паралельного алгоритму для задач із паралелізмом даних
« Назад
1. Мета роботи: розробка і реалізація паралельного алгоритму для задач із паралелізмом даних. 2. Склад робочого місця: - Обладнання: IBM-сумісний персональний комп'ютер. - Програмне забезпечення: операційна система Windows, Java 2 SDK версії 1.2.2 або вище. 3. Короткі теоретичні відомості 3.1. Основні положення Паралелізмом, або багатозадачністю називається властивість систем, коли декілька процесів обчислення відбуваються водночас, і, можливо, взаємодіють один з одним. За принципом організації багатозадачності, виділяють такі типи систем з паралелізмом: - Конвеєрні системи - декілька спеціалізованих блоків одночасно працюють над частинами одного потоку команд. - Паралельні системи, у яких множина команд однієї програми одночасно виконується на декількох АЛП або процесорах. В залежності від принципів організації оперативної пам'яті системи поділяють на такі види: 1. Обчислювальні системи зі спільною пам'яттю - Common Memory Systems або Shared Memory Systems. Як видно з назви, такі системи мають спільну пам'ять, що виявляються в спільному адресному просторі для всіх процесорів, що займаються виконанням команд однієї програми. Якщо один процесор запише якесь значення у певну комірку пам'яті, то інший процесор зможе напряму отримати доступ до тієї ж комірки і безперешкодно зчитати або змінити її значення. 2. Обчислювальні системи з розподіленою пам'яттю - Distributed Memory Systems. В даних системах кожен процесор має свою локальну пам'ять з локальним адресним простором. Для таких систем характерна наявність швидких каналів, що зв'язують пам'ять з відповідним процесором. Обмін даними між процесорами відбувається в таких системах з допомогою пересилки повідомлень через центральний комунікатор. 3.2. Реалізація багатозадачності з використанням мови програмування Java Багатозадачність в Java реалізує модель системи зі спільною пам'яттю. Основною обчислювальною одиницею є так званий «потік». Програма на мові Java може складатись з декількох (не менше одного) потоків, які виконуються паралельно і мають спільний адресний простір. Будь-яка програма за замовчуванням вже має один потік - так званий головний потік (Main Thread), з якого починається виконання програми. В процесі свого функціонування програма може ініціювати створення нових потоків та завершувати існуючі. Програма вважається «живою» поки живий хоча б один її потік. Створити потік можна двома способами: 1. Створити клас, що наслідує клас Thread і перевизначити метод run(). 2. Створити екземпляр класу Thread і передати йому як параметр щось, що реалізує інтерфейс Runnable, що містить один метод - run(). Обидва методи приводять до однакового результату і можуть використовуватися на рівні залежності від зручності використання того чи іншого способу в умовах конкретної задачі. Для того щоб виконати код, який міститься в методі run() у паралельному потоці потрібно викликати метод start() класу Thread, який ініціює створення потоку та починає виконання відповідного коду. Класс Thread має цілу низку методів для роботи з потоками, які будуть детально розглянуті в лабораторній роботі №2. Для виконання ж даної роботи буде достатньо розглянути лише деякі з них: - start() - як вже говорилось, створює новий потік та запускає на виконання відповідний код. - destroy() - знищує потік без очищення даних, що до нього відносяться. - join() - зупиняє виконання потоку, який викликав даний метод до завершення виконання потоку, для якого було викликано join. Іншими словами join змушує один потік чекати завершення обчислень в іншому. Даний метод використовується, наприклад, при організації паралельних обчислень, коли після виконання роботи у всіх потоках потрібно провести агрегацію результатів та сформувати остаточну відповідь. Так як потік автоматично завершується по закінченню набору інструкцій, які він мав виконати, потрібно якось змусити потік-агрегатор дочекатись завершення робочих потоків, щоб отримати результати роботи, для чого і доцільно використати join(). 3.3. Приклад Далі наведено приклад програми, яка паралельно рахує скалярний добуток векторів: package threadlab; /** * * @author sds */ class ThreadCacl extends Thread{
double vectA[]; double vectB[]; int startIndex; int endIndex; double result;
public ThreadCacl(double[] vectA, double[] vectB, int startIndex, int endIndex) { this.vectA = vectA; this.vectB = vectB; this.startIndex = startIndex; this.endIndex = endIndex; }
public double getResult() { return result; }
@Override public void run(){ for(int i = startIndex; i<endIndex; i++ ){ result+=vectA[i]*vectB[i]; } }
}
public class ThreadSample { public static int SIZE = 1000; public static int NUNMBER_JOBS = 7; public static void main(String [] args ) throws InterruptedException{
double vectA[] = new double [SIZE]; double vectB[] = new double [SIZE];
for(int i =0; i<SIZE; i++){ vectA[i]=i; vectB[i]=1; }
double serialResult =0; for( int i=0; i< SIZE; i++){ serialResult+=vectA[i]*vectB[i]; }
System.out.println(serialResult);
ThreadCacl TreadArrray[] = new ThreadCacl[NUNMBER_JOBS];
for(int i = 0; i < NUNMBER_JOBS; i++){
TreadArrray[i] = new ThreadCacl(vectA ,vectB, SIZE/NUNMBER_JOBS * i, i==NUNMBER_JOBS-1 ?SIZE:SIZE/NUNMBER_JOBS * (i + 1) ); TreadArrray[i].start(); } for(int i = 0; i < NUNMBER_JOBS; i++){ TreadArrray[i].join(); } double parallelResult = 0; for(int i = 0; i < NUNMBER_JOBS; i++){ parallelResult += TreadArrray[i].getResult(); }
System.out.println(parallelResult); } } Розробити послідовну на багатопоточну програми які реалізують варіант індивідуального завдання. Зберегти час розрахунку. Порівняти правильність виконання, порівнявши послідовний та паралельний розв’язки. Розрахувати коефієнт прискорення та коефіцієнт ефективності для декількох різних значень кількості потоків та розміру векторів або кроків інтегрування. 1. Створити 2 вектора з N>=1000 елементами з випадкових чисел. Скласти ці вектори. 2. Створити 2 вектора з N>=1000 елементами з випадкових чисел. Скалярно помножити ці вектори. 3. Створити вектор з N>=1000 елементами з випадкових чисел. Знайти максимальний та мінімальний елементи векторів. 4. Створити вектор з N>=1000 елементами з випадкових чисел. Знайти норму 5. Створити вектор з N>=1000 елементами з випадкових чисел. Знайти евклідову норму вектора 6. Створити вектор з N>=1000 елементами з випадкових чисел. Знайти норму 7. Створити двовимірний масив розмірності n×m. Знайти максимальне і мінімальне значення масиву. 8. Створити двовимірний масив розмірності n×m. Знайти суму елементів масиву. 9. Створити квадратну матрицю n×n та вектор розмірності n, n>=100; написати паралельну програму множення матриці на вектор. 10. Виконати транспонування матриці n×n. 11. Заповнити квадратну матрицю випадковими числами. На головній діагоналі розмістити суми елементів, які лежать в тому ж рядку і стовпці. 12. Заповнити квадратну матрицю випадковими числами. Відобразити симетрично відносно вертикальної вісі сектори матриці, які лежать праворуч та ліворуч головної і побічної діагоналей. 13. Заповнити квадратну матрицю випадковими числами. Відобразити верхню половини матриці на нижню дзеркально симетрично відносно горизонтальної вісі. 14. Заповнити матрицю випадковими числами. Відобразити праву половину матриці на ліву дзеркально симетрично відносно вертикальної вісі. 15. Виконати інтегрування функції 16. Виконати інтегрування функції 17. Виконати інтегрування функції 18. Виконати інтегрування функції
Питання для самоконтролю
1. Процеси та потоки. 2. Методи run(), start(), join() потоку. 3. Визначення паралелізму. 4. Класифікація Фліна (паралельних обчислювальних систем). 5. Класифікація систем за типом оперативної пам’яті. 6. Коефіцієнти прискорення та ефективності. 7. Закон Амдела. 8. Продуктивність та пікова продуктивність паралельних обчислювальних систем. 9. Чому коефіцієнт прискорення може бути меншим за 1? З повагою ІЦ "KURSOVIKS"! |
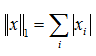вектора.
.
.
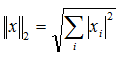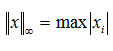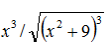методом прямокутників з вузлом зліва, відрізок [2;3], результат перевірити зі значенням первісної 
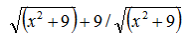. Кроки інтегрування взяти 0.001, 0.0001.
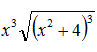методом прямокутників з вузлом справа, відрізок [3;5], результат перевірити зі значенням первісної 
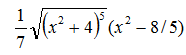. Кроки інтегрування взяти 0.001, 0.0001.
методом прямокутників з вузлом у середній точці, відрізок [0.5;2], результат перевірити зі значенням первісної 
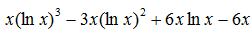. Кроки інтегрування взяти 0.001, 0.0001.
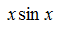методом трапецій, відрізок [-1.5;1.5], результат перевірити зі значенням первісної 
. Кроки інтегрування взяти 0.001, 0.0001.