Методичні вказівки до лабораторної роботи на тему Вступ до системи MATLAB
|
« Назад Призначення і сфера застосування математичного пакета MATLAB. Для розв’язання прикладних задач важливим є застосування засобів автоматизації обчислень від простих до досить громіздких, а також графічна візуалізація отриманих результатів. Сучасне програмне забезпечення ПЕОМ має досить різноманітні, потужні математичні пакети, наприклад, MATLAB, MAPLE, MATHEMATICA, які використовуються у математичних обчисленнях і аналітичних перетвореннях. Пакет MATLAB є інтерактивною системою з розвиненою довідковою системою, містить велику кількість операторів та функцій, застосування яких дає змогу чисельно розв’язувати складні задачі математики, фізики, хімії, інженерії, фінансів [1-3,5-8,10]. Крім вбудованих засобів, пакет можна доповнювати власними розробками, використовуючи як власну мову (М-програми), так і зовнішні алгоритмічні мови, наприклад, С#, JAVA. Підсумовуючи, охарактеризуємо спектр задач, які розв’язуються за допомогою пакета MATLAB: - проведення математичних досліджень, що вимагають обчислень і аналітичних розрахунків; - розробка і аналіз алгоритмів; - математичне моделювання, комп’ютерний експеримент; - аналіз і обробка даних; - візуалізація, наукова та інженерна графіка; - розробка графічних і розрахункових додатків. Перше знайомство з роботою в системі. Для практичної роботи будемо використовувати програмний комплекс MATLAB 7, робота в якому досить легка та комфортна. При стандартному завантаженні (клацнувши мишею по ярлику програми MATLAB) на екрані відкривається система меню та три вікна: робоча область, вікно історії, командне вікно. Робота з меню здійснюється за допомогою маніпулятора миша та набору певних клавіатурних комбінацій (“гарячих клавіш ”). У вікні робочої області відображаються імена змінних, уведених користувачем, та їх поточні значення. Вікно історії використовується для зберігання та відображення раніше виконаних команд користувача. Інтерактивний сеанс роботи в командному вікні MATLAB прийнято іменувати сесією (session). Сесія, по суті, є поточним документом, що відображає роботу користувача із системою MATLAB. У ній є рядки введення даних, результатів і повідомлень про помилки. За допомогою команд сесії користувач взаємодіє із середовищем пакета. Поіменовані дані поточної сесії, розташовані в робочій області пам'яті (але не саму сесію), можна записати на диск у вигляді файлів формату .mat, використовуючи команду save (зберегти). Командою load (завантажити) можна відновити з диска дані робочої області. Фрагменти сесії можна зберегти в певному документі за допомогою команди diary. При роботі з MATLAB у командному режимі діє найпростіший рядковий редактор. Команди, які використовуються в редакторі, мають, як правило, відповідні комбінації клавіш для їх виклику. Ці комбінації наведені в табл. 1.1. Таблиця 1.1. Комбінації клавіш для команд рядкового редактора
Раніше введені команди автоматично утворюють список, який виводиться у вікні історії. Якщо з'явилася необхідність повторити раніше виконану команду, то треба відшукати її в цьому вікні і двічі клацнути по ній лівою кнопкою миші. Для активізації вікна історії необхідно вибрати вкладку з однойменною назвою і клацнути по ній лівою кнопкою миші. Якщо клацнути на команді вікна історії лівою кнопкою миші, то дана команда стає поточною (на синьому тлі). Можна виділити потрібну послідовність команд за допомогою комбінації клавіш <Shift+↑>, <Shift+↓>. Вставлений у командний рядок набір команд відправляється на виконання натисненням клавіші <Enter>. До цього вміст набору можна редагувати, використовуючи звичайні прийоми редагування, спільні для Windows-програм, у тому числі за допомогою миші. Можна вносити в команди необхідні зміни, видаляти зайві команди і додавати нові. ОПЕРАЦІЙНЕ СЕРЕДОВИЩЕ MATLAB І ОСНОВНІ КОМАНДИТеоретичні відомості Основні пункти меню системи, інструментальна панель і опції MATLAB. Основне меню системи складається з 6 пунктів, кожний з яких у свою чергу містить декілька підпунктів різного ступеня вкладеності : - File – робота з файлами; - Edit – редагування сесії та документів М-файлів; - View – управління вікнами та панеллю інструментів; - Web – доступ до Інтернет-ресурсів; - Windows – відображення відкритих додаткових вікон, перехід до потрібного вікна; - Help — доступ до довідкових підсистем. Розглянемо призначення деяких із них. Серед команд меню File: New – відкриття підменю з пунктами: - M-file – відкриття вікна редагування М-файлів, аналог команди edit; - Figure – відкриття порожнього вікна графіки; - Model – відкриття порожнього вікна для створення Simulink-моделі; - GUI – відкриття вікна розробки елементів графічного інтерфейсу користувача; - Open – відкриття вікна завантаження файла; - Close Command Windows – закриття вікна командного режиму; - Import data – відкриття вікна імпорту файлових даних; - Save Workspace As – відкриття вікна запису робочої області у вигляді файла із заданим ім’ям; - Set Path – відкриття вікна встановлення шляхів доступу файлової системи; - Preferences – відкриття вікна налаштування елементів інтерфейсу; - Print – відкриття вікна друку поточного документа; - Print Selection – відкриття вікна друку виділеної частини документа. - Exit – завершення роботи в системі. Серед команд менюEdit: - Undo – скасування результату попередньої операції; - Redo – скасування дії останньої операції Undo; - Cut – вирізання виділеного фрагмента і перенесення його в буфер обміну; - Copy – копіювання виділеного фрагмента в буфер обміну; - Paste – вставка фрагмента з буфера обміну в поточну позицію курсору; - Select All – виділення всієї сесії; - Delete – видалення виділеного об'єкта; - Clear Command Windows – очистка тексту сесії зі збереженням створених об'єктів, аналог команди clc; - Clear Command History – очистка вікна історії команд; - Clear Workspace – очистка вікна робочої області. Вікно управління редактора М-файлів. Для підготовки і редагування М-файлів (текстів програм на внутрішній алгоритмічній мові системи) використовується спеціальний системний редактор текстів або зовнішній текстовий редактор. Редактор можна викликати командою edit з командного рядка або через пункт меню File. Після закінчення роботи з текстом М-файла його необхідно записати на диск, використовуючи команду Filе → Save as у меню редактора. При створенні тексту файла редактор виконує ретельну синтаксичну перевірку. Редактор має й інші важливі засоби – він дозволяє встановлювати в тексті М-файла спеціальні мітки переривання (breakpoints). При досягненні цих міток обчислення припиняються, і користувач може оцінити проміжні результати обчислень, наприклад, значення певних змінних, перевірити правильність виконання циклів і т.д. Для зручності роботи з редактором рядки програми в ньому нумеруються в послідовному порядку. Редактор є багатовіконним. Вікно кожної програми оформлене як вкладка. Управління командним вікном. Розглянемо деякі команди управління вікном командного режиму: - clс – очистка екрана і розміщення курсору в лівому верхньому куті порожнього вікна; - home – повернення курсору в лівий верхній кут вікна; - echo<file_name> on – увімкнення режиму збереження команд, які вводяться на екрані, в текстовий файл <file_name>(файл М-сценарію); - echo <file_name> off – вимкнення попереднього режиму збереження команд; - echo <file_name> – зміна режиму збереження на протилежний; - echo on all – увімкнення режиму виведення на екран тексту для всіх М-файлів; - echo off all – вимкнення режиму виведення на екран тексту М-файлів; - mоrе on – увімкнення режиму посторінкового виведення (відображення) (корисний при перегляді великих М-файлів); - mоrе off – вимкнення режиму посторінкового виведення, в цьому випадку для перегляду великих файлів треба користуватися смугою прокручування. MATLAB у ролі калькулятора. Система MATLAB створена таким способом, що будь-які (часом досить складні) обчислення можна виконувати в режимі прямих обчислень (інтерактивному режимі), тобто без підготовки програми. Це перетворює MATLAB у надзвичайно потужний калькулятор, здатний здійснювати не тільки звичайні для калькуляторів обчислення (наприклад, виконувати арифметичні операції й обчислювати елементарні функції), але й операції з векторами й матрицями, комплексними числами, рядами й поліномами і т.д. Можна майже миттєво задати й вивести графіки різних функцій — від простої одновимірної до складної тривимірної фігури. Робота із системою в режимі прямих обчислень носить діалоговий характер і відбувається за правилом “поставив запитання, отримав відповідь”. Користувач набирає певний запит на клавіатурі, потім (якщо потрібно) редагує його в командному рядку і передає на виконання натисненням клавіші <Enter>. Деякі правила роботи: - ознакою готовності системи до введення запиту є наявність курсору після символу “>>” у командному вікні; - дані вводяться і редагуються за допомогою найпростішого рядкового редактора; - записи запитів розрізняються залежно від використання великих і малих літер; - якщо в кінці запиту (команди) поставити знак “;”, то результат (відповідь) не відображається у командному вікні. Якщо цього не зробити (в тому числі і в М-файлі), то після успішного обчислення буде здійснене виведення результатів на екран; - якщо не зазначена змінна для отримання результату обчислень, то MATLAB призначає таку змінну з ім'ям ans ; - знаком присвоювання є “=” ; - результат обчислень виводиться в рядках відображення (без знака “>>” ); - у загальному випадку для подання результату в командному вікні застосовується така форма: <ім’я_змінної> = <результат>. - вбудовані функції записуються малими літерами, і їхні аргументи вказуються в круглих дужках, наприклад, sin(x). Вихід із системи. Завершення роботи з системою MATLAB здійснюється за допомогою команд quit, exit або натисненням комбінації клавіш <Ctrl+0>. У деяких випадках математичний вираз, що вводиться, може виявитись настільки довгим, що для нього не вистачить одного рядка. Тоді для його перенесення на новий рядок використовується символ “...” (три або більше крапки), наприклад: s = 1 – 1/2 + 1/3– 1/4 + 1/5 – 1/6 + 1/7 ... 1/8 + 1/9 – 1/10 + 1/11 – 1/12 . Цей прийом може бути корисним для створення наочних документів (запобігання заходу рядків у невидиму область вікна або текстового документа, який друкується на принтері). Загалом кажучи, максимальне число символів в одному рядку командного режиму – 4096, а в М-файлі – не обмежене, проте з такими довгими рядками працювати незручно. У ранніх версіях пакета рядок мав не більше 256 символів. Типи даних, які використовуються в MATLAB. Усі типи даних, з структурної точки зору, є масивами, тому в системі MATLAB:
Надалі будемо розглядати роботу тільки з такими типами даних: double – натуральні, цілі, дійсні і комплексні дані; char – лінійний масив (рядок). Звичайно в MATLAB є й інші типи даних: sparse,uint8, cell, structта інші. Константи, змінні, імена спеціальних змінних. Як і в інших алгоритмічних мовах константи використовуються для позначення незмінних величин. Вони не мають імен, а тип константи визначається при її запису, наприклад, 1, –25, 435.123, –2.345, 1е–12, 1.26E8, ‘значення змінної X = ’. Змінна – це певна поіменована величина, яка здатна зберігати деякі, звичайно різні за значеннями, дані відповідних типів. Тип змінної заздалегідь не декларується, а визначається виразом, значення якого привласнюється змінній. Серед поіменованих констант виділяють системні змінні, які мають фіксовані імена і значення. Основні системні змінні, що використовуються в системі MATLAB, наведені в табл. 2.1. Таблиця 2.1. Системні змінні MATLAB
Системні змінні можна перевизначити, але це можливо лише під час поточної сесії. У системі MATLAB для іменування змінних використовуються ідентифікатори, які обов’язково починаються з букви і можуть містити букви, цифри й символ підкреслення “_”. Ідентифікатор може мати скільки завгодно символів, але значущими є тільки 31 перший (початковий) символ. Побудова виразів. Як і в алгоритмічній мові, вирази використовуються для запису послідовності певних обчислень над даними. Зазвичай чітко визначається пріоритет їх виконання, як для групи операцій, так і всередині групи. До першої категорії (найвищий пріоритет в обчисленнях) відносяться арифметичні операції, до другої – відношення, до третьої – логічні операції. Операції і спеціальні символи, які використовуються при записі виразів, наведені в табл. 2.2. Таблиця 2.2. Операції і спеціальні символи у виразах MATLAB
В арифметичних операціях використовуються дані однакової розмірності. Якщо один із операндів є скаляром, а інший ні, то скаляр розширюється до розмірів другого операнда. Набір арифметичних операцій у MATLAB складається із стандартних операцій додавання, віднімання, множення, ділення, піднесення до степеня і доповнений спеціальними матричними операціями (табл. 2.3). У табл. 2.4 наведений порядок виконання арифметичних операцій. Таблиця 2.3. Арифметичні операції MATLAB
Таблиця 2.4. Ієрархія при виконанні арифметичних операцій
Операції відношення (табл.2.5) мають два операнди і використовуються для порівняння двох величин, векторів або матриць (в алгоритмічній мові – предикатів). Таблиця 2.5. Операції відношення
При обчисленні предиката ми отримуємо результат 1 – Істина або 0 – Хибність. Примітка. Оператори “<”, “<=”, “>”, “>=” при порівнянні комплексних чисел порівнюють лише їх дійсні частини. Логічні операції і функції (табл. 2.6) застосовуються поелементно до даних і використовуються для побудови булевих виразів. Таблиця 2.6. Логічні операції і функції
Пакет MATLAB містить значну кількість елементарних і спеціальних функцій (табл. 2.7 – 3.14). Зі списком елементарних функцій можна ознайомитись за допомогою команди help elfun, а зі списком спеціальних функцій – за допомогою команди help specfun. Функції можуть бути вбудованими (внутрішніми) і зовнішніми, або M–функціями. Зовнішні функції містять свої визначення в M–файлах. Вбудовані функції зберігаються у відкомпільованому ядрі системи MATLAB, внаслідок чого вони виконуються гранично швидко. Таблиця 2.7. Тригонометричні та гіперболічні функції
Таблиця 2.8. Трансцендентні функції
Таблиця 2.9. Функції роботи з комплексними числами
Таблиця 2.10. Функції заокруглення і модульна арифметика
Таблиця 2.11. Теоретико-числові функції
Таблиця 2.12. Функції для роботи з рядками символів
Таблиця 2.13. Функції часу та дати
Таблиця 2.14. Функції для операцій з елементами матриць
Таблиця 2.15. Функції для роботи з матрицями
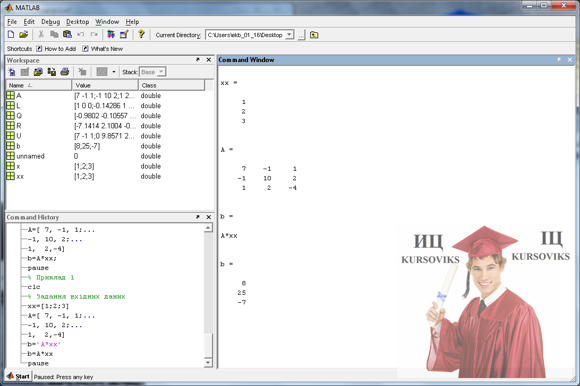
3) На практиці обчислення оберненої матриці в явному вигляді не так вже й необхідне. Цю операцію застосовують при розв’язанні системи лінійних рівнянь вигляду Ах=b. Дійсно, один із шляхів – обчислення x=inv(A)*b. Але кращим (з погляду мінімізації часу розрахунку) є використання оператора матричного ділення х=А\ b. Ця операція використовує метод виключення Гаусса без явного формування оберненої матриці. Приклад 1. Нижче наведено приклад, в якому формуються матриця A і вектор xx; знаходиться вектор b – добуток матриці A на вектор xx; розв’язується СЛАР Ax=b з використанням QR- і LU-розкладів матриці A. Знати зміст кожного рядка тексту! % Приклад 1 clc % Задання вхідних даних xx=[1;2;3]; A=[ 7, -1, 1;... -1, 10, 2;... 1, 2,-4] b=A*xx pause
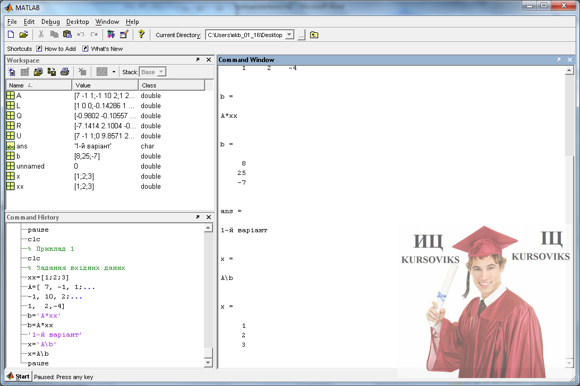
% 1-й варіант x=A\b pause
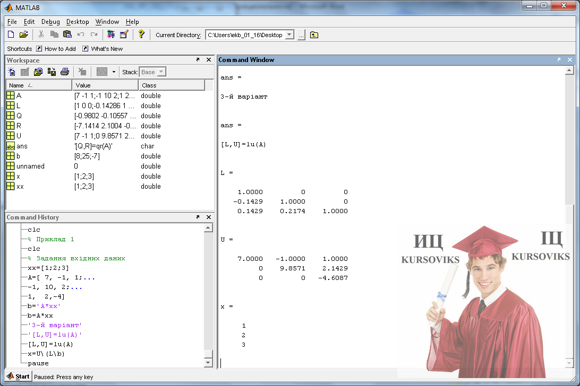
% 2-й варіант [Q,R]=qr(A); % Перевірте Q*Q' i Q'*Q x=R\(Q'*b) pause % 3-й варіант [L,U]=lu(A); x=U\(L\b) pause Розглянемо приклади: Приклад 1 Приклад 1 Варіант 1 Приклад 1 Варіант 2
Приклад 1 Варіант 3 З повагою ІЦ "KURSOVIKS"! |