Методичні рекомендації до лабораторної роботи №7 на тему Дослідження моделі Еванса та застосування до розв’язання економічних задач
« НазадМетодичні рекомендації до лабораторної роботи №7 на тему Дослідження моделі Еванса та застосування до розв’язання економічних задачМета: отримати навички застосування моделі Еванса до розв’язання задач. Теоретичні відомості6. МОДЕЛИ ЭВАНС А УС ТАНОВЛЕНИЯ РАВНОВЕСНОЙ ЦЕНЫ НА РЫНКЕ ОДНОГО ТОВАРА6.1. Модель Эванса с непрерывным временем6.1.1. Исходные положенияИзучаемая модель основана на следующих положениях: 1. Цена товара является функцией от времени 2. Предложение является функцией от цены товара в момент времени t и определяется формулой где a и b- известные положительные числа. 3. Спрос является функцией от цены товара в момент времени t и определяется формулой где c и d- известные положительные числа. 4. Считается, что цена товара выражается через спрос и предложение по формуле где у - известное положительное число. 5. В момент времени t = 0 цена товара известна и равна р0. Требуется найти равновесную цену товара. 6.1.2. Расчетное уравнениеОсновываясь на положениях, перечисленных в параграфе 6.1.1., составим расчетное уравнение модели: которое является линейным неоднородным дифференциальным уравнением первого порядка с постоянными коэффициентами. Общее решение уравнения (6.1.1) имеет вид где а - произвольное число. Требуется найти решение уравнения (6.1.2), удовлетворяющее начальному условию С этой целью подставим в формулу (6.1.2) значение t = 0: Следовательно, и решение задачи Коши (6.1.1). (6.1.3) имеет вид: Переходя в формуле (6.1.4) к пределу при где символом 6.2. Модель Эванса с дискретным временем6.2.1. Исходные положенияИзучаемая модель основана на следующих положениях: 1. Товар поступает на рынок в течение k равных промежутков времени, где k - натуральное число. 2. Цена товара в течение одного промежутка времени не изменяется и обозначается символами p1,p2,…,pk. в периоды времени 1,2,…,k, соответственно. 3. Предложение зависит от цены товара в предыдущем промежутке времени и вычисляется по формуле где a и b - известные положительные числа. и решение задачи Коши (6.1.1), (6.1.3) имеет вид: Переходя в формуле (6.1.4) к пределу при где символом 4. Спрос зависит от цены товара в текущем промежутке времени и вычисляется по формуле где c и d - известные положительные числа. 5. В начальный момент времени цена товара известна и равна р0. Требуется найти равновесную цену товара. Замечание. Рассматриваемую модель называют также моделью установления равновесной цены на рынке с запаздыванием предложения. 6.2.2. Расчетные уравненияОсновываясь на равенстве спроса и предложения, составим следующее рекуррентное уравнение модели: Преобразуем уравнение (6.2.1) к более удобному виду: Введем новую переменную по формуле: где В результате уравнение (6.2.2) примет следующий вид: Если теперь в качестве числа выбрать число то уравнение (6.2.5) преобразуется к следующему виду: Формула (6.2.7) задаст геометрическую прогрессию с первым членом у0 и знаменателем - b/d. Поэтому. откуда с помощью формул (6.2.4) и (6.2.6) получаем: Формула (6.2.9) определяет равновесную цену товара в течение промежутка времени с номером i=1,2,…, если известна начальная цена товара р0. В случае, когда который носит название предельной равновесной цены. Исследование модели завершено. З повагою ІЦ "KURSOVIKS"! |
















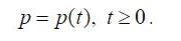
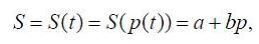
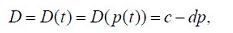
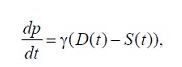
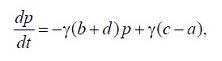 (6.1.1)
(6.1.1)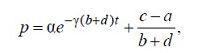 (6.1.2)
(6.1.2)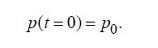 (6.1.3)
(6.1.3)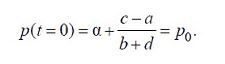
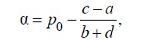
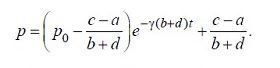 (6.1.4)
(6.1.4)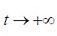 , получим соотношение
, получим соотношение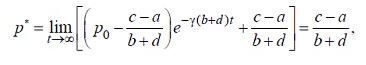 (6.1.5)
(6.1.5)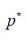 обозначена предельная равновесная цена. Исследование модели завершено.
обозначена предельная равновесная цена. Исследование модели завершено.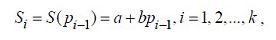
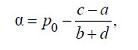
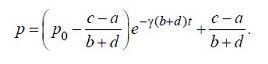 (6.1.4)
(6.1.4)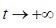 , получим соотношение
, получим соотношение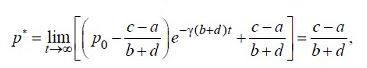 (6.1.5)
(6.1.5)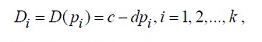
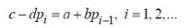 (6.2.1)
(6.2.1)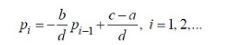 (6.2.2)
(6.2.2)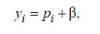 (6.2.3)
(6.2.3)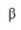 - некоторое число, которое определим чуть позже, и совершим в уравнении (6.2.2) замену переменных
- некоторое число, которое определим чуть позже, и совершим в уравнении (6.2.2) замену переменных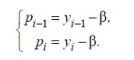 (6.2.4)
(6.2.4)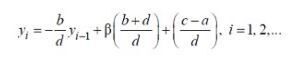 (6.2.5)
(6.2.5)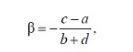 (6.2.6)
(6.2.6)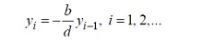 (6.2.7)
(6.2.7)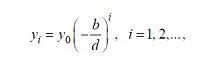 (6.2.8)
(6.2.8)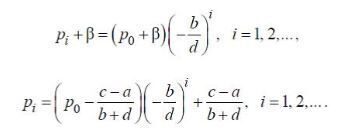 (6.2.9)
(6.2.9)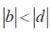 , существует предел равновесных цен товара:
, существует предел равновесных цен товара: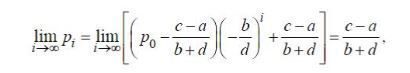 (6.2.10)
(6.2.10)