Методичні рекомендації до лабораторної роботи №6 на тему Дослідження моделі поведінки споживача та визначення функції попиту
« НазадМетодичні рекомендації до лабораторної роботи №6 на тему Дослідження моделі поведінки споживача та визначення функції попитуМета: отримати навички дослідження поведінки споживача та побудови функції попиту. Хід роботиТеоретичні відомостіФункція корисності та її властивостіВведення функції корисності дозволяє замінити відношення переваги звичними відношеннями між числами: більше, менше, дорівнює. У теорії споживання припускаються гіпотези і вважається, що функція корисності має такі властивості: 1) 2) 3) 4) Умова 3 зазвичай використовується у більш широкому трактуванні — як матриця других похідних (матриця Гессе) і є від’ємно визначеною. Гранична корисність товару показує, на скільки зростає корисність, якщо кількість товару зростає в малому обсязі. Поверхнею байдужості називають поверхню, на якій корисність постійна: або має диференціальну форму: Умова (1) означає, що дотична до поверхні байдужості перпендикулярна градієнтові корисності. Це означає (з погляду споживача) можливість заміни одного товару певною кількістю іншого (рівноцінного) товару. Нехай в (1) dxi = 0 для i = 3, …, n, тоді це співвідношення має вигляд: звідси тобто гранична норма заміщення першого товару другим дорівнює відношенню граничної корисності першого та другого товарів. Норма заміщення показує, скільки необхідно одиниць другого товару, щоб замінити малий обсяг першого товару, який вибув. Бюджетною множиною називають множину тих наборів товарів, які може придбати споживач, маючи дохід обсягом M: де p = (p1, …, pn) — вектор-рядок цін. У теорії споживання вважається, що споживач завжди прагне максимізувати корисність, і єдине, що його стримує, — це обмежений дохід. Тому математичною моделлю споживача є модель (3): Ця задача на умовний екстремум зводиться до знаходження безумовного екстремуму функції Лагранжа: Необхідні умови локального екстремуму: Це дійсно визначає точку максимуму, бо матриця Гессе— від’ємно визначена. З (5) бачимо, що споживач за фіксованого доходу так обирає набір x*, що в цій точці відношення граничної корисності дорівнює відношенню цін: Звідси, як наслідок, випливає 2-й закон Госсена: гранична корисність, що припадає на грошову одиницю, витрачену на даний товар, має дорівнювати граничним корисностям, що припадають на грошову одиницю, витрачену на інші товари. Чим більшою кількістю блага ми володіємо, тим меншу цінність має для нас кожна додаткова одиниця цього блага. Наприклад, споживач, що потерпає від спраги, із задоволенням вип'є першу склянку пепсі-коли. Друга склянка принесе йому менше задоволення, ніж перша, третя - менше, ніж друга. І так буде відбуватися доти, поки гранична корисність чергової склянки не буде дорівнювати нулю. Хоча загальна корисність зростає, гранична корисність при цьому падає, що призводить до уповільнення зростання загальної корисності. Таким чином, корисність блага визначається не загальною, а граничною його корисністю для споживача. Оскільки із зростанням споживання гранична корисність економічного блага для споживача знижується, то виробник може продати додаткову кількість своєї продукції лише в тому разі, якщо знизить ціну. Закон зменшення граничної корисності лежить в основі визначення попиту. Правило максимізації корисності полягає в тому, що можна максимізувати корисність, якщо розподілити грошовий дохід таким чином, щоб остання грошова одиниця (грн.), витрачена на перший продукт, а також остання грошова одиниця (грн.), витрачена на другий продукт і так далі, принесуть однакову кількість додаткової чи граничної корисності. Інакше це можна сформулювати так: відношення граничної корисності блага до його ціни має бути однаковим для всіх благ. Якщо розв’язати систему (4)-(5) відносно x*, отримаємо функцію попиту споживача: Рівновага споживача відповідає такій комбінації товарів, яка максимізує корисність при даних бюджетних обмеженнях. Така рівновага передбачає, що щойно споживач отримає цей набір товарів, у нього зникає стимул змінювати цей набір на інший. Рухаючись уздовж бюджетного обмеження, споживач може знайти точку, яка б відповідала максимальному задоволенню його потреб, тобто, відповідала б найбільшій корисності. Така точка належить найвищій кривій байдужості, яка може бути досягнута в межах цього бюджету. На рис.1 такою точкою буде точка D - точка дотику кривої байдужості U2 до бюджетної лінії. Крива байдужості U3, яка є кривою, яка відповідає вищому рівню задоволення потреб (вищому рівню корисності), ніж крива байдужості U2, не може бути досягнута, бо виходить за межі бюджету. Точка дотику найвищої кривої байдужості і лінії бюджетного обмеження відповідає стану споживчої рівноваги (рис. 1). Рис. 1 - Споживча рівновага в залежності від кривої байдужості та лінії бюджетного обмеження
Перелік питань до захисту лабораторної роботи
1. Висловіть записи:
2. В чому полягає раціональна поведінка споживача?
3. Дайте означення функції корисності. Перерахуйте властивості функції корисності.
4. Сформулюйте перший закон Госсена.
5. Сформулюйте другий закон Госсена.
6. В чому полягає вивчення поведінки споживача?
7. Що таке простір товарів і який його опис?
8. Як визначити граничну корисність товару (блага)?
9. Як обчислити граничну норму заміщення одного товару (блага) іншим?
10. Яка функція називається опуклою?
11. Якою має бути матриця Гессе, щоб функція корисності була опуклою?
12. Як знайти точку споживчої рівноваги?
13. Запишіть математичну модель поведінки споживача, виходячи з його раціональної поведінки.
14. Запишіть функцію Лагранжа для моделі споживача та необхідні умови локального екстремуму функції Лагранжа.
15. Як визначити функцію попиту з моделі поведінки споживача? Функцією яких чинників є функцію попит?
З повагою ІЦ "KURSOVIKS"! |
















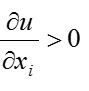 — зі зростанням споживання блага корисність зростає;
— зі зростанням споживання блага корисність зростає; — невеликий приріст блага за його початкової відсутності різко збільшує корисність;
— невеликий приріст блага за його початкової відсутності різко збільшує корисність;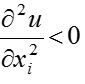 — зі зростанням споживання блага швидкість зростання корисності зменшується (1-й закон Госсена);
— зі зростанням споживання блага швидкість зростання корисності зменшується (1-й закон Госсена);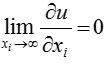 — коли є дуже великий обсяг блага, його подальше зростання не приводить до зростання корисності.
— коли є дуже великий обсяг блага, його подальше зростання не приводить до зростання корисності.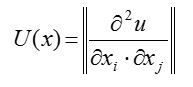
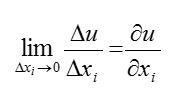
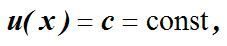
 (1)
(1)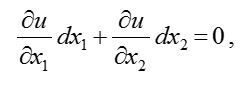
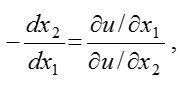 (2)
(2)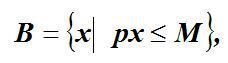
 (3)
(3)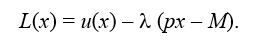
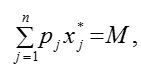 (4)
(4)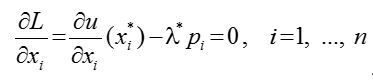 . (5)
. (5)
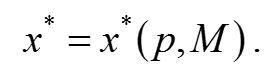 (6)
(6)