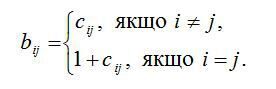Методичні рекомендації до лабораторної роботи №4 на тему Балансові моделі, Модель міжгалузевого балансу Леонтьєва
« НазадМетодичні рекомендації до лабораторної роботи№4 на тему Балансові моделі, Модель міжгалузевого балансу ЛеонтьєваМета роботи: навчитись використовувати модель міжгалузевого балансу Леонтьєва до аналізу економічної системи. Хід роботиТеоретичні відомостіОснову інформаційного забезпечення моделі міжгалузевого балансу становить технологічна матриця, що містить коефіцієнти прямих матеріальних витрат на виробництво одиниці продукції. Ця матриця є базою економіко-математичної моделі міжгалузевого балансу. Припускається, що для виробництва одиниці продукції в j-й галузі необхідна певна кількість витрат проміжної продукції і-ї галузі, що становить aij, і ця величина не залежить від обсягів виробництва в j-й галузі та є досить стабільною величиною в часі. Величини aij називають коефіцієнтами прямих матеріальних витрат та обчислюють таким чином: Коефіцієнти прямих матеріальних витрат показують, яку частку продукції і-ї галузі необхідно витратити, якщо враховувати лише прямі витрати, для виробництва одиниці продукції j-ї галузі. З урахуванням формули (9) систему рівнянь балансу (7) можна записати у вигляді Якщо ввести до розгляду матрицю коефіцієнтів прямих матеріальних витрат А = (аij), вектор-стовпець валової продукції X та вектор-стовппець кінцевої продукції Y: то система рівнянь (10) у матричній формі матиме вигляд Систему рівнянь (2), чи у матричній формі (3), називають моделлю міжгалузевого балансу (моделлю Леонтьєва, моделлю «витрати — випуск»). За допомогою цієї моделі можна виконати три варіанти обчислень: 1) задаючи в моделі обсяги валової продукції кожної галузі (Хi), можна визначити обсяги кінцевої продукції кожної галузі (Yi): Y = (E – A)X, де Е — одинична матриця n-го порядку; 2) задаючи обсяги кінцевої продукції всіх галузей (Yi), можна визначити обсяги валової продукції кожної галузі (Хi): X = (E – A)–1Y; де (Е – А)–1 — матриця, обернена до матриці (Е – А). 3) для низки галузей задаючи обсяги валової продукції, а для решти — обсяги кінцевої продукції, можна відшукати величини кінцевої та валової продукції всіх галузей. Якщо визначник матриці (Е – А) не дорівнює нулеві, тобто ця матриця не вироджена, тоді існує матриця, обернена до неї. Позначимо цю матрицю через В: B = (Е – А)–1. Систему рівнянь у матричній формі (11) можна записати:X = BY . (4) Елементи матриці В позначатимемо через bij , тоді з матричного рівняння (4) для будь-якої і-ї галузі можна отримати співвідношення: Із співвідношення (5) випливає, що валова продукція постає як зважена сума обсягів кінцевої продукції, ваговими коефіцієнтами тут є bіj, котрі показують, скільки всього необхідно виробити валової продукції і-ї галузі для випуску у сферу кінцевого використання одиниці продукції j-ї галузі. На відміну від коефіцієнтів прямих витрат aij , коефіцієнти bіj називають коефіцієнтами повних матеріальних витрат, і вони включають у себе як прямі, так і опосередковані витрати всіх порядків. Якщо прямі витрати відбивають кількість засобів виробництва, використаних безпосередньо на виготовлення певних обсягів даного продукту, то опосередковані стосуються попередніх стадій виробництва і входять у виробництво продукції не прямо, а через інші (проміжні) засоби виробництва. Коефіцієнти повних матеріальних витрат bij показують, який обсяг продукції j-ї галузі необхідно виробити, щоб з урахуванням прямих і опосередкованих витрат цієї продукції отримати одиницю кінцевої продукції j-ї галузі. Коефіцієнти повних матеріальних витрат можна застосовувати, коли необхідно визначити, як вплинуть на валовий випуск певної галузі деякі зміни щодо обсягів випуску кінцевої продукції всіх галузей: де DXi та DYj — зміни (прирости) обсягів валової й кінцевої продукції відповідно. Поняття продуктивної матриціЗдійснюючи аналіз моделі міжгалузевого балансу, потрібно розглянути основні властивості матриці коефіцієнтів прямих матеріальних витрат А. Ці коефіцієнти за визначенням є невід’ємними, отже, матриця А в цілому є невід’ємною: А ³ 0. Процес відтворення не можна було б здійснити, якщо б для власного відтворення в галузі витрачався більший обсяг продукту, ніж створювався. Звідси очевидно, що діагональні елементи матриці А менші ніж одиниця: aii <1, i = 1, ..., n. Система рівнянь міжгалузевого балансу відображає реальні економічні процеси, в яких сенс можуть мати лише невід’ємні значення валових випусків; таким чином, вектор валової продукції складається з невід’ємних компонентів вектора Х, який є невід’ємним вектором: X > 0. Постає питання, за яких умов економічна система здатна забезпечити невід’ємний кінцевий випуск у всіх галузях? Відповідь на це питання пов’язана з поняттям продуктивної матриці коефіцієнтів прямих матеріальних витрат. Означення. Називатимемо невід’ємну матрицю А продуктивною, якщо існує такий невід’ємний вектор Х, що X > AX. (7) Очевидно, що умова (7) означає існування невід’ємного вектора кінцевої продукції Y > 0 для моделі міжгалузевого балансу (3). Щоб матриця коефіцієнтів прямих матеріальних витрат А була продуктивною, необхідно і достатньо, аби виконувалася одна з перелічених нижче умов: 1) матриця (Е – А ) має бути невід’ємно оберненою, тобто повинна існувати обернена матриця (Е – А) –1 ³ 0; 2) матричний ряд 3) найбільший за модулем розв’язок 4) усі головні мінори матриці (Е – А), тобто визначники матриць, що утворені елементами перших рядків і перших стовпчиків цієї матриці порядку від 1 до n, мають бути додатними. Більш простою, але лише достатньою ознакою продуктивності матриці А є обмеження на величину її норми, тобто на величину найбільшої із суми елементів матриці А в кожному стовпчику. Якщо норма матриці А строго менша від одиниці, то ця матриця є продуктивною. Наголосимо, що дана умова є лише достатньою, і матриця А може виявитися продуктивною й у разі, якщо її норма буде більшою за одиницю. Найбільший за модулем корінь характеристичного рівняння, наведеного в третій умові продуктивності матриці А (позначимо його через Проаналізуємо матрицю коефіцієнтів повних матеріальних витрат, тобто матрицю В = (Е – А)–1. Елемент цієї матриці bij показує, скільки всього необхідно виробити продукції і-ї галузі, щоб одержати одиницю кінцевої продукції j-ї галузі. Дамо інше означення коефіцієнта повних матеріальних витрат з огляду на те, що окрім прямих витрат існують опосередковані витрати тієї чи іншої продукції для виробництва продукції даної галузі. Розглянемо для прикладу формування витрат електроенергії на випуск стального прокату, обмежуючись технологічним ланцюжком «руда—чавун—сталь—прокат». Витрати електроенергії для отримання прокату зі сталі називатимемо прямими витратами, ті самі витрати для отримання сталі з чавуну — опосередненими витратами 1-го порядку, а витрати електроенергії для отримання чавуну з руди — опосередкованими витратами електроенергії на випуск сталевого прокату 2-го порядку тощо. Отже, можна дати таке означення: Коефіцієнтом квазіповних матеріальних витрат cij називають суму прямих і опосередкованих витрат продукції і-ї галузі для виробництва одиниці продукції j-ї галузі через проміжні продукти на всіх попередніх стадіях виробництва. Якщо коефіцієнти опосередкованих матеріальних витрат k-го порядку позначати через a якщо ввести до розгляду матрицю коефіцієнтів квазіповних матеріальних витрат C = (cij) та матриці коефіцієнтів опосередкованих матеріальних витрат різних порядків З огляду на змістовну суть коефіцієнтів опосередкованих матеріальних витрат можна записати такі математичні співвідношення: за використання котрих матрична формула (11.15) набирає вигляду Якщо матриця коефіцієнтів прямих матеріальних витрат А є продуктивною, то з другої умови продуктивності існує матриця Порівнюючи вирази (16) та (17), дістанемо: В = Е + С, або в поелементному записі: Це визначає економічний сенс, що пояснює відмінність між коефіцієнтами (елементами) матриць В та С: на відміну від коефіцієнтів матриці С, що враховують лише витрати на виробництво продукції, коефіцієнти матриці В включають у себе, окрім витрат, також одиницю кінцевої продукції, котра виходить за сферу виробництва.
Питання до захисту практичної роботи
1. Що являє собою модель міжгалузевого балансу Леонтьєва?
2. Що являє собою технологічна матриця?
3. Яка матриця називається продуктивною матрицею?
4. Як можна довести, що матриця коефіцієнтів прямих матеріальних витрат є продуктивною?
5. Як обчислюються коефіцієнти прямих матеріальних витрат?
6. Що таке характеристичне рівняння матриці і як обчислити власні значення?
7. Як обчислюються коефіцієнти повних матеріальних витрат?
8. Які різновиди досліджень можна проводити за допомогою моделі Леонтьєва?
9. Як обчислити матрицю коефіцієнтів повних матеріальних витрат засобами Excel, якщо задана матриця коефіцієнтів прямих матеріальних витрат?
10. Як обчислити вектор валового продукту засобами Excel, якщо задана матриця коефіцієнтів прямих матеріальних витрат та вектор кінцевого продукту?
11. Як обчислити вектор кінцевого продукту засобами Excel, якщо задана матриця коефіцієнтів прямих матеріальних витрат та вектор валового продукту?
З повагою ІЦ "KURSOVIKS"! |
















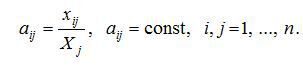 (1)
(1) (2)
(2)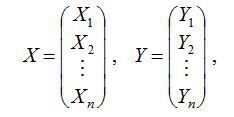
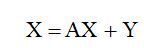 . (3)
. (3) (5)
(5)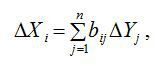 (6)
(6)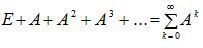 має збігатися,
має збігатися, 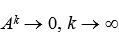 , а його сума дорівнює оберненій матриці (Е – А)–1;
, а його сума дорівнює оберненій матриці (Е – А)–1; (власне значення) характеристичного рівняння
(власне значення) характеристичного рівняння  має бути строго меншим від одиниці:
має бути строго меншим від одиниці:  ;
; характеризує залишок після витрат, тобто продуктивність. Чим більшим є
характеризує залишок після витрат, тобто продуктивність. Чим більшим є  , то має місце формула
, то має місце формула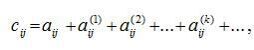 (16)
(16)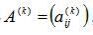 , то поелементну формулу (17) можна подати в матричній формі:
, то поелементну формулу (17) можна подати в матричній формі: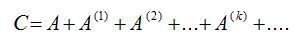 (17)
(17)
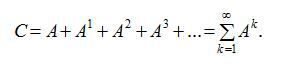 (18)
(18)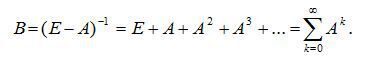 (19)
(19)