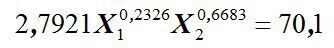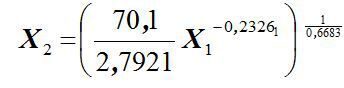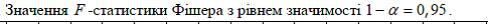Методичні рекомендації до лабораторної роботи №1 на тему Побудова двофакторної виробничої функції, економетричної моделі економічної системи
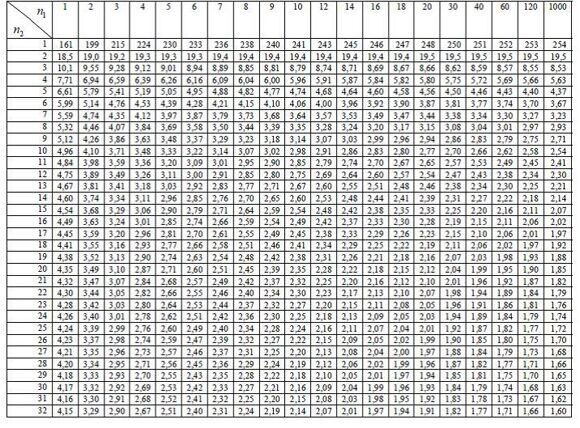
« Назад
Методичні рекомендації до лабораторної роботи №1 на тему Побудова двофакторної виробничої функції, економетричної моделі економічної системиМета: отримати навички побудови виробничої функції та застосування її до аналізу економічної системи. 1-2. Розглянемо виконання пунктів 1-2 завдання на прикладі статистичних даних, наведених у табл. 1 Щоб зробити необхідні розрахунки, приведемо логарифмуванням задану функцію до лінійного виду: Таблиця 1 Вихідні дані та розрахунки
Всі обчислені значення Y1, Z1, Z2 знаходяться у таблиці 1. До отриманих даних Z1, Z2 та Y1, застосуємо функцію ЛИНЕЙН. Вона за методом найменших квадратів (1МНК) знаходить значення невідомих КОЕФІЦІЄНТІВ РЕГРЕСІЇ (1) (див. довідку). Ця функція вводиться в масив комірок і завершувати її введення потрібно з Ctrl+Shift+Enter. Отримаємо:
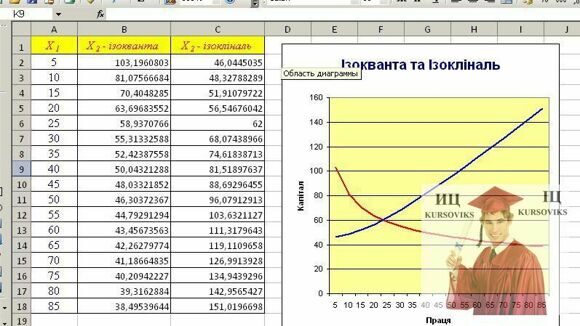
У цій таблиці a1=0,668256, a2=0,232594, lna0=1,026804. В результаті обчислень ми отримали наступну модель: або повертаючись до вихідної форми: 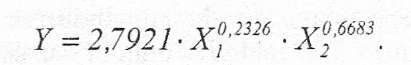 Перевіримо адекватність моделі експериментальним даним. Для цього знайдемо значення критерію Фішера на рівні значимості а = 0,95 та степенями свободи[1]. Так як Для перевірки значущості коефіцієнтів 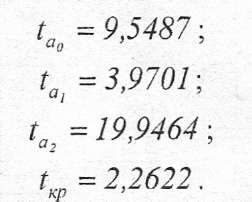 Так як всі відповідні значення 3. 1-3.5 Див.Лекц.№2 4. Для випадку статистичних даних табл.1, побудуємо ізокванту для Y = 70,1. Розв’яжемо це рівняння відносно Х2: Обчислення виконати в Excel і побудувати графік. Див. Рис.1.
Рис. 1 - Побудова ізокванти Побудова ізокліналі, що проходить через точку (25; 62) представлена на рис.2.
Рис. 2 - Побудова ізокліналі На рис.3 зображені ізокванта та ізокліналь в одній системі координат.
Рис 3 - Ізокванта та ізокліналь. Перетинаються під кутом 90 градусів
ДОДАТОК
Варіанти завдань до лабораторної №1_МЕ
 [1] Див. довідку по додатковій регресійній статистиці функції ЛИНЕЙН(известные_значения_y;известные_значения_x;конст;статистика): «В выходных данных функции ЛИНЕЙН величины F и df используются для оценки вероятности получения наибольшего значения F. Величина F может сравниваться с критическими значениями в публикуемых таблицах F-распределения или FРАСП Excel может быть использована для вычисления возможности получения наибольшего значения F. Соответствующее F-распределение имеет степени свободы v1 и v2. Если величина n представляет количество точек данных и величина const имеет значение ИСТИНА или опущено, то v1 = n – df – 1 и v2 = df. (При const = ЛОЖЬ v1 = n – df and v2 = df). Функция Excel FРАСП(F, v1, v2) возвращает вероятность получения наибольшего значения F.» [2] Див.Додаток у кінці роботи. З повагою ІЦ "KURSOVIKS"! |
(1)
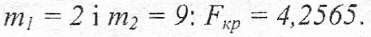
[2], то отримана модель достовірна з ймовірністю 0,95.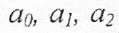
знайдемо спочатку критичне значення критерію Стьюдента на рівні значимості a= 0,95 та порівняємо його із значеннями критерію Стьюдента для коефіцієнтів 
то всі коефіцієнти достовірні з ймовірністю 0,95.
