49 Задачи с курса Физика на тему 18, Качение твердых тел. Работа и энергия при вращении и качении твердых тел (65 задач) 10.11.2018 22:37

Задача 18.1

Экспериментатор стоит на скамье Жуковского и держит ось вращающегося колеса так, что оси колеса и скамьи (круглой платформы) совпадают (платформа при этом не вращается). Момент инерции колеса относительно его оси I₁ = 0,500 кг•м²; угловая скорость ω=15 c^-1. Момент инерции экспериментатора и платформы относительно ее оси I₂ = 3,00 кг•м^2. Моментом инерции колеса относительно оси, совпадающей с его диаметром, и трением в осях платформы и колеса пренебречь.

а) Какую работу А совершит экспериментатор, повернув ось колеса на 90⁰? На 180⁰? б) В Чем состоит причина изменения момента импульса системы «экспериментатор на платформе — колесо» при поворачивании колеса?

 

Задача 18.2

Пуля массой m = 50 г, двигаясь со скоростью v = 100 м/с, ударяется о выступ зубчатого колеса, момент инерции которого 0,2 кг•м^2. Расстояние от точки попадания пули до оси вращения R = 30 см. Определить угловую скорость колеса, если 80% энергии пули уходит на его вращение. Удар считать неупругим.

 

Задача 18.3

Расположенный вертикально однородный стержень длины 1 может вращаться вокруг горизонтальной оси, проходящей через один из его концов. В точку, отстоящую от оси вращения на 2*l/3, ударяется тело массы m, летящее перпендикулярно к стержню и к оси. После удара стержень отклоняется на угол α, а тело отскакивает назад со скоростью v. Найти начальную скорость тела v_o. Масса стержня М.

 

Задача 18.4

Человек, стоящий на скамье Жуковского, ловит вытянутой рукой мяч массой т, летящий перпендикулярно руке с горизонтальной скоростью v_o, считая что момент инерции скамьи с человеком I₀, длина руки и положение ее не меняется, определить угловую скорость и изменение механической энергии системы.

 

Задача 18.5

Однородный стержень может вращаться в вертикальной плоскости относительно горизонтальной оси, проходящей через его конец. Стержень приводят в горизонтальное положение и отпускают. Определить угловую скорость и линейную скорость нижнего конца стержня в тот момент, когда он образует угол α с горизонталью. Длина стержня 1.

 

Задача 18.6

Человек стоит на краю платформы, вращающейся с угловой скоростью ω₁= 6 рад/с. Какую работy совершит человек при переходе в центр платформы. если масса платформы m₁ = 100 кг, ее радиус R = 6, масса человека m₂ = 70 кг, момент инерции человека относительно вертикальной оси, проходящей через его центр масс, I₀ =2кг*м². Платформу считать однородным диском.

 

Задача 18.7

Столб высотой h = 3,0 м из вертикального положения падает на землю. Определить момент импульса L столба относительно точки опоры и скорость верхнего конца столба v в момент удара о землю. Масса столба m = 50 кг, его нижний конец не смещается.

 

Задача 18.8

Радиус вала махового колеса r =10^-2 м. На вал намотан шнур, к концу которого привязан груз m = 0,2 кг. Под действием силы тяжести груз опускается за 5 секунд с высоты h_l = 1,2 м, а затем, вследствие вращения колеса, по инерции поднимается на высоту h₂ =0,8.Определить момент инерции колеса.

 

Задача 18.9

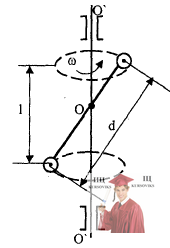
Рис. 18.1 – Момент импульса L системы

Найти момент импульса L системы, изображенной на рисунке, относительно точки О. Система вращения без трения вокруг оси O’O' с иловой скоростью ω. К оси O’O' приложен момент сил М удерживающий ее в неизменном положении. Чему равен модyль изменения момента импульса │ΔL│за полоборота? Какую работу А совершает момент сил М при повороте на угол φ?

 

Задача 18.10

Определить кинетическую энергию вращающегося на токарном станке полого стального цилиндра длиной I =400 мм. Внутренний и наружный радиусы цилиндра r_вн= 300 мм и r_нар= 500 мм. Число оборотов станка n= 120 об/мин.

 

Задача 18.11

Диск, насаженный на ось радиусом r (маятник Масквелла), подвешивается на двух нитях одинаковой длины, привязанных к концам оси. Нити симметрично в один ряд наматывают на ось, диск при этом поднимается, а затем его свободно отпускают. Определить угол поворота φ диска вокруг его оси как функцию времени t, если при t = 0 имеемφ= 0 и ω = dφ/dt = 0. Найти время τ, в течение которого диск опускается с высоты h. Масса диска вместе с осью равна m, а их момент инерции I.

 

Задача 18.12

Шар скатывается по наклонной плоскости длиной l = 7 м с углом наклона α = 30⁰. Определить скорость шара (скорость центра инерции v_c) в момент выхода на горизонтальный участок. Указать, при каком условии скатывание происходит без скольжения.

 

Задача 18.13

Рис. 18.2 – Качение катушки без проскальзывания под действием горизонтальной силы

При каком минимальном коэффициенте трения µ возможно качение катушки без проскальзывания под действием горизонтальной силы F, приложенной в точке В (см. рисунок)? Радиусы катушки R_l и R₂, ее масса m, момент инерции относительно оси симметрии І_о.

 

Задача 18.14

Решить задачу 18.13 считая. что горизонтальная сила F приложена к точке А катушки. Найти действующую на катушку силу трения и полное ускорение верхней точки катушки при качении без проскальзывания. При каком внутреннем радиусе катушки R_i действующая на нее сила трения покоя обращается в нуль?

 

Задача 18.15

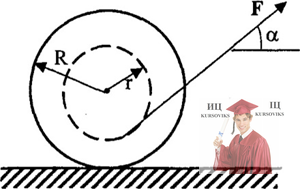
Рис. 18.3 – Горизонтальной плоскости лежит катушка ниток

На горизонтальной плоскости лежит катушка ниток массы m (см. рисунок). Момент инерции катушки относительно ее оси 1. Катушку тянут за нить с силой Р, как показано на рисунке. а) При каких углах α между силой и горизонтом катушка будет двигаться ускоренно в сторону натянутой нити? б) Какой должна быть сила F для того, чтобы отсутствовало скольжение ? Коэффициент трения между катушкой и плоскостью равен µ. в) Катушка движется ускоренно без скольжения в сторону натянутой нити. Найти в этом случае работу А, которую совершила сила F за время t от начала движения.

 

Задача 18.16

С вершины наклонной плоскости начинает скатываться сплошной однородный цилиндр. Найти время скатывания цилиндра, если начальная высота h = 3 м, а длина наклонной плоскости l = 10 м .

 

Задача 18.17

Какую часть от полной кинетической энергии составляет кинетическая энергия вращения для катящихся без скольжения тел: а) цилиндра; б) шара; в) обруча?

 

Задача 18.18

Однородный цилиндр радиуса R скатывается без скольжения с наклонной плоскости, составляющей с горизонтом угол α. Угловая скорость вращения цилиндра ω. Найти время τ, за которое yигловая скорость возрастает вдвое.

 

Задача 18.19

Обод массой m = 2 кг и радиусом 5 см скатывается по наклонной плоскости длиной l= 2 м и углом наклона α= 30 ^0. Определить его момент инерции относительно оси вращения, если скорость в конце наклонной плоскости v = 2 м/с.

 

Задача 18.20

Шар и цилиндp одинаковой массой, двигаясь с одинаковой скоростью, вкатываются вверх по наклонной плоскости. Какое из тел поднимется выше? Найти отношение высот подъема.

 

Задача 18.21

Шар и сплошной цилиндр имеют одинаковую массу m = 5 кг и катятся с одинаковой скоростью м/с. Найти кинетические энергии этих тел.

 

Задача 18.22

Диск катится в течение 3с и останавливается, пройдя расстояние 10м. Определить коэффициент трения, считая его постоянным.

 

Задача 18.23

Рис. 18.4 – Маятник Максвелла ось которого подвешена на двух накрученных на нее нитях

Маятник Максвелла представляет собой массивный диск, ось которого подвешена на двух накрученных на нее нитях (см. рисунок). Если маятник отпустить, то он будет совершать возвратно-поступательное движение в вертикальной плоскости при одновременном вращении диска вокруг оси. Определить ускорение поступательного движения маятника, полагая, что момент инерции оси равен нулю.

 

Задача 18.24

Рис. 18.5 – Массивный металлический диск укрепленный на легком стержне скатывается по наклонному желобу

Массивный металлический диск радиусом R, укрепленный на легком стержне радиусом r, скатывается по наклонному желобу так, как показано на рисунке. Высота желоба h, длина 1.

l) Показать, что соотношение между кинетическими энергиями поступательного и вращательного движений со временем изменяться не будет.

2) Определить, при каком соотношении между радиусом R и r кинетическая энергия вращательного движения в n раз больше энергии поступательного (моментом инерции стержня пренебречь).

3) Определить время опускания стержня при отсутствии потерь на трение.

 

Задача 18.25

С какой скоростью должен въехать велосипедист в нижнюю точку мертвой петли, чтобы не сорваться вниз? Масса велосипедиста с велосипедом m = 90 кг, масса обоих колес m₁ = 6 кг. Трением пренебречь, колеса считать ободьями.

 

Задача 18.26

Однородный стержень, падавший в горизонтальном положении с высоты h, упруго ударился одним концом о край массивной плиты. Найти скорость центра стержня сразу после удара.

 

Задача 18.27

Рис. 18.6 – Цилиндры скатываются без проскальзывания с высоты по наклонной плоскости

Оси сплошного и полого цилиндров с равными массами m связаны жесткой штангой. Цилиндры скатываются без проскальзывания с высоты h по наклонной плоскости образующей угол α с горизонтом. Найти время скатывания и силу, возникающую в штанге. Массой штанги пренебречь.

 

Задача 18.28

На гладком горизонтальном столе лежит однородный длинный стержень. В конец стержня ударяет небольшой кубик, движущийся по поверхности стола в направлении, перпендикулярном оси стержня со скоростью v_o. Найти скорость кубика после абсолютно упругого удара о стержень. Масса кубика в п раз меньше массы стержня.

 

Задача 18.29

Катящийся без проскальзывания по столу обруч ударяется об идеально гладкую вертикальную стенку. Считая удар абсолютно упругим, доказать, что через некоторое время после удара обруч остановится. Найти это время, если начальная скорость центра обруча v_o. коэффициент трения скольжения µ. Трением качения пренебречь.

 

Задача 18.30

Сплошной однородный цилиндр раскрутили до угловой скорости ω₀ вокруг его оси и положили на наклонную шероховатую плоскость. На какую максимальную высоту может подняться цилиндр? Угол наклона плоскости с горизонтом α, коэффициент трения µ.

 

Задача 18.31

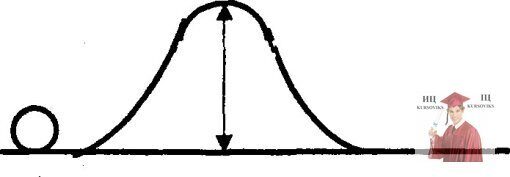
Рис. 18.7 – На горизонтальном столе находится горка

На горизонтальном столе находится горка массой m, высотой h (см. рисунок). По столу в направлении горки катится сплошной однородный цилиндр. При какой минимальной скорости центра масс v_o цилиндр сможет преодолеть горку? Считать, что качение цилиндра все время происходит без проскальзывания. Рассмотреть случаи: а) 10рка неподвижна; б) горка может без трения перемещаться по столу. Масса цилиндра mо.

 

Задача 18.32

В покоящийся на горизонтальном столе однородный шар массой m₁, попадает горизонтально летящая пуля массой m₂ и застревает в нем. Скорость пули в момент удара направлена в центр масс шара. Через некоторое время после удара качение шара становится равномерным. Найти установившуюся скорость центра масс шара. Скорость пули перед ударом v_o. Считать, что m₁ >> m₂.

 

Задача 18.33

Равномерно катящийся по горизонтальному столу однородный шар ударяется о такой же неподвижный шар. Через некоторое время после удара качение обоих шаров становится равномерным, причем центр масс первого шара движется со скоростью u₁. Считая удар шаров абсолютно упругим, найти начальную скорость центра масс второго шара.

 

Задача 18.34

Шар и сплошной цилиндр, изготовленные из одного и того же материала, одинаковой массы катятся без скольжения с одинаковой скоростью. Определить, во сколько раз кинетическая энергия шара меньше кинетической энергии сплошного цилиндра.

 

Задача 18.35

Полная кинетическая энергия Т диска, катящегося по горизонтальной поверхности. равна 24 Дж. Определить кинетическую энергию Т₁, поступательного и Т₂ вращательного движения диска.

 

Задача 18.36

Полый тонкостенный цилиндр массой m= 0,5 кг, катящийся без скольжения, ударяется о стены и отскакивает от нее. Скорость цилиндра до удара о стену v₁=1,4 м/с, после удара v’₁=1 м/с. Определить выделившееся при ударе количество теплоты Q.

 

Задача 18.37

К ободу однородного сплошного диска массой m = 10 кг, насаженного на ось, приложена постоянная касательная сила F = 30 Н. Определить кинетическую энергию диска через время t = 4 с после начала действия силы.

 

Задача 18.38

Вентилятор вращается с частотой n= 600 об/мин. После выключения он начал вращаться равнозамедленно и, сделав N= 50 оборотов, остановился. Работа А сил торможения равна 31,4 Дж. Определить:1) момент М сил торможения; 2) момент инерции І вентилятора.

 

Задача 18.39

Маховик в виде сплошного диска, момент инерции которого I= 1,5 кг•м², вращаясь при торможении равнозамедленно, за время t-==1 мин уменьшил частоту своего вращения с n₀=240 об/мин до n₁ = 120 об/мин. Определить: 1) угловое ускорение ε маховика; 2) момент М силы торможения; З) работу торможения А.

 

Задача 18.40

Колесо радиусом R = 30 см и массой m = 3 кг скатывается по наклонной плоскости длиной l = 5 м и углом наклона α = 25 ^0. Определить момент инерции колеса, если его скорость v в конце движения составляла 4,6м/с.

 

Задача 18.41

С наклонной плоскости, составляющей угол α= 30⁰ с горизонтом, скатывается без скольжения шарик. Пренебрегая трением, определить время движения шарика по наклонной плоскости, если известно, что его центр масс при скатывании понизился на 30 см.

 

Задача 18.42

Полый тонкостенный цилиндр катится вдоль горизонтального участка со скоростью v = l,5 м/с. Определить путь, который он пройдет в гору за счет кинетической энергии, если Уклон горы равен 5м на каждые 100 м пути.

 

Задача 18.43

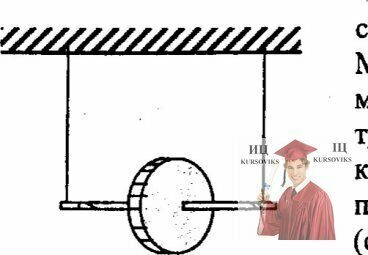
Рис. 18.8 – Массивный диск туго насаженный на ось

Для демонстрации законов сохранения применяется маятник Максвелла, представляющий собой массивный диск радиусом R и массой m, туго насаженный на ось радиусом r, которая подвешивается на двух предварительно намотанных на нее нитях (см. рисунок). Когда маятник отпускают, то он совершает возвратно-поступательное движение в вертикальной плоскости при

одновременном движении диска вокруг оси. Не учитывая сил сопротивления и момента инерции оси, определить: 1) ускорение поступательного движения маятника; 2) силу натяжения нити.

 

Задача 18.44

Однородный шар радиусом r = 20 см скатывается без скольжения с вершины сферы радиусом R = 50 см. Определить угловую скорость ω шара после отрыва от поверхности сферы.

 

Задача 18.45

Маховик начинает вращаться из состояния покоя с постоянным угловым ускорением ε= 0,4 рад/с². Определить кинетическую энергию маховика через время t₂ = 25 с после начала движения, если через t₁= 10 с после начала движения момент импульса L₁ маховика составлял 60 кг•м²/с.

 

Задача 18.46

Человек массой m = 60 кг, стоящий на краю горизонтальной платформы радиусом R =1 м и массой М = 120 кг, вращающейся по инерции вокруг неподвижной вертикальной оси с частотой n₁ = 10 мин^-1 переходит к ее центру. Считая платформу круглым однородным диском, а человека - точечной массой, определить работу, совершаемую человеком при переходе от края платформы к ее центру.

 

Задача 18.47

Шарик массой m = l00 г. привязанный к концу нити длиной l₁ = 1 м, вращается, опираясь на горизонтальную плоскость. с частотой n₁ =1c^-1 Нить укорачивается и шарик приближается к оси вращения до расстояния l₂=0.5м. С какой частотой n₂ будет при этом вращаться шарик? Какую работу А совершит внешняя сила, укорачивая нить? Трением шарика о плоскость пренебречь.

 

Задача 18.48

Маховик вращается по закону, выражаемому уравнением φ= А + Bt²+ Ct², где А = 2 рад, В = 32 рад/с, С = -4 рад/с ^2. Найти среднюю мощность ˂N˃ развиваемую силами, действующими на маховик при его вращении, до остановки, если его момент инерции I = 100 кг•м ².

 

Задача 18.49

Маховик вращается по закону, выражаемому уравнением φ = А + Bt² + Ct^2, где А = 2 рад, В = 16 рад/с, С = - 2 рад/с^2. Момент инерции I маховика равен 50 кг•м^2. Найти законы, по которым меняются вращающий момент М и мощность N. Чему равна мощность в момент времени t = 3 с?

 

Задача 18.50

Якорь мотора вращается с частотой n=1500 мин^-1. Определить вращающий момент М, если мотор развивает мощность N = 500 Вт.

 

Задача 18.51

Со шкива диаметром d = 0,48 м через ремень передается мощность N = 9 кВт. Шкив вращается с частотой n= 240 мин^-1. Сила натяжения Т₁, ведущей ветви ремня в два раза больше силы натяжения Т₂ ведомой ветви. Найти силы натяжения обеих ветвей pемня.

 

Задача 18.52

Для определения мощности мотора на его шкив диаметром d = 20 см накинули ленту. К одному концу ленты прикреплен динамометр, к другому подвесили груз Р. Найти мощность N мотора, если мотор вращается с частотой n= 24 с^-1, масса m груза равна 1 кг и показание динамометра F = 24 Н.

 

Задача 18.53

Маховик в виде диска массой m = 80 кг и радиусом R = 30 см находится в состоянии покоя. Кактю работу А₁ нужно совершить, чтобы сообщить маховику частоту n = 10 с^-1. Какую работу А₂ пришлось бы совершить, если бы при той же массе диск имел меньшую толщину, но вдвое больший радиус?

 

Задача 18.54

Кинетическая энергия Т вращающегося маховика равна 1 кДж. Под действием постоянного тормозящего момента маховик начал вращаться равнозамедленно и, сделав N = 80 оборотов, остановился. Определить момент М силы торможения.

 

Задача 18.55

Маховик, момент инерции которого равен 40 кг•м^2, начал вращаться равноускоренно из состояния покоя под действием момента силы М = 20 Н•м. Вращение продолжалось в течение t = 10 с. Определить кинетическую энергию Т, приобретенную маховиком.

 

Задача 18.56

Пуля массой m = 10 г летит со скоростью v = 800 м/с, вращаясь около продольной оси с частотой n= 3000 1/c. Принимая пулю за цилиндрик диаметром d — 8 мм, определить полную кинетическую энергию Т пули.

 

Задача 18.57

Сплошной цилиндр массой m= 4 кг катится без скольжения по горизонтальной поверхности. Линейная скорость v оси цилиндра равна 1 м/с. Определить полную кинетическую энеррию Т цилиндра.

 

Задача 18.58

Обруч и сплошной цилиндр, имеющие одинаковую массу m = 2 кг, катятся без скольжения с одинаковой скоростью v =5 м/с. Найти кинетические энергии этих тел.

 

Задача 18.59

Шар катится без скольжения по горизонтальной поверхности. Полная кинетическая энергия Т шара равна 14 Дж. Определить кинетическую энергию Т₁, поступательного Т₂ вращательного движения шара.

 

Задача 18.60

Определить линейную скорость v центра шара, скатившегося без скольжения с наклонной плоскости высотой h = 1 м.

 

Задача 18.61

Сколько времени t будет скатываться без скольжения обруч с наклонной плоскости длиной l= 2 м и высотой h = 10 см?

 

Задача 18.62

Тонкий прямой стержень длиной l=1 м прикреплен к горизонтальной оси, проходящей через его конец. Стержень отклонили на угол φ=60⁰ от положения равновесия и отпустили. Определить линейную скорость v нижнего конца стержня в момент прохождения через положение равновесия.

 

Задача 18.63

Рис. 18.9 – Однородный тонкий стержень свободно вращается а вокруг горизонтальной оси Z, проходящей через точку О

Однородный тонкий стержень длиной l= 1 м может свободно вращаться а вокруг горизонтальной  оси Z, проходящей через точку О на стержне (см. рисунок). Стержень отклонили от положения равновесия на угол α и отпустили. Определить угловую скорость в ω стержня и линейную скорость v точки В на стержне в момент прохождения им положения равновесия. Вычисления выполнить для следующих случаев:1)a-0, b=1/2, α=π/3; 2) a=1/3,b=21/3/ α=π/2;3)a=1/4, b=1, α=2π/3.

 

Задача 18.64

Карандаш длиной l = 15 см, поставленный вертикально, падает на стол. Какую угловую ω и линейную v скорости будет иметь в конце падения: 1) середина карандаша? 2) верхний его конец? Считать, что трение настолько велико, что нижний конец карандаша не проскальзывает.

 

Задача 18.65

Рис. 18.10 – Однородный диск радиусом R=20 см может свободно вращаться вокруг горизонтальной оси Z

Однородный диск радиусом R=20 см может свободно вращаться вокруг горизонтальной оси Z, перпендикулярной плоскости диска и проходящей через точку О (см. рисунок). Определить угловую скорость ω стержня и линейную скорость v точки В на диске в момент прохождения им положения равновесия. Вычисления выполнить для следующих случаев: 1) а =b= R, α=π/2; 2) a=R/2, b=0 α=π/3; 3) a=2R/3, b=2R/3, α=5π/6; 4) a=R/3, b=R, α=2π/3.

С уважением ИЦ "KURSOVIKS"!