Задачи с курса Физика на тему 17, Основное уравнение динамики вращательного движения (28 задач)

48 Задачи с курса Физика на тему 17, Основное уравнение динамики вращательного движения (28 задач) 10.11.2018 22:31

Задача 17.1

Расположенный горизонтально однородный цилиндр массы М и радиуса R начинает вращаться без трения вокруг своей оси под действием груза массы m, прикрепленного к легкой нити, намотанной на цилиндр. Найти время t, за которое груз опустится с высоты h.

 

Задача 17.2

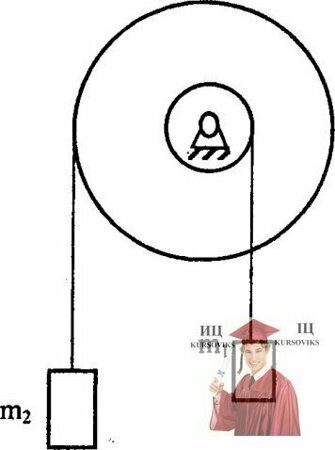
Рис. 17.1 – К концам намотанных на ступенчатый блок идеальных нитей прикреплены два груза

К концам намотанных на ступенчатый блок идеальных нитей прикреплены два груза массами m₁= 1 кг и m₂ = 3 кг (см. рисунок). Радиусы шкивов блока R_l = 0,1 м и R₂ = 0,2 м. Найти ускорения грузов. Моменты инерции блока относительно оси вращенияI₀ = 0,15 кг•м^2. Трением пренебречь.

 

Задача 17.3

Два точечных груза, массы которых равны m₁=1 кг и m₂ = 2 кг, соединены жестким стержнем длиной l = 1м. Система может вращаться в вертикальной плоскости относительно горизонтальной оси, проходящей через середину стержня. Стержень приводят в горизонтальное положение и отпускают. С какой силой стержень действует на ось в начальный момент? Каково угловое ускорение стержня в момент, когда он образует угол α= 30⁰ с вертикалью?

 

Задача 17.4

На массивный блок, насаженный на неподвижную ось, намотана нерастяжимая нить. к концу которой прикреплен груз массой m = 1кг. Ускорение груза при движении оказалось равным а = 2 м/c². Найти массу блока, считая его однородным сплошным цилиндром. Массой нити и трением пренебречь.

 

Задача 17.5

Однородный стержень может вращаться в вертикальной плоскости относительно горизонтальной оси, проходящей через его конец. Стержень приводят в горизонтальное положение и отпускают. С какой силой действует стержень на ось в первоначальный момент? Каково угловое ускорение стержня в тот момент. когда он образует угол α с вертикалью? Масса стержня m. Длина l.

 

Задача 17.6

На горизонтальную ось насажен маховик со шкивом радиусом R. На шкив намотана нить, к концу которой прикреплен груз массой m. Опускаясь равноускоренно, груз прошел путь S за время t. Найти момент инерции маховика. Трением пренебречь.

 

Задача 17.7

Через блок перекинута идеальная нить, к концам которой прикреплены грузы массами m₁ и m₂. Система приводится в движение. Ускорение каждого из грузов оказалось равным а. Определить массу блока. Блок считать сплошным однородным круговым цилиндром; трением пренебречь.

 

Задача 17.8

Диск массы m = 0,500 кг и диаметра d = 400 мм вращается с угловой скоростью ω= 157 с^-1. При торможении он останавливается в течение t = 10,0 с. Найти среднюю величину тормозящего момента М.

 

Задача 17.9

Маховик раскрутили до угловой скорости ω₀ и предоставили самому себе. Действующий на маховик момент сил трения равен М_тр. Найти момент инерции маховика І, если известно, что маховик остановился через t секунд.

 

Задача 17.10

Обруч раскрутили вокруг оси симметрии, перпендикулярной его плоскости, до некоторой угловой скорости и положили плашмя на шероховатый стол. Найти момент силы трения и угловое ускорение замедленного вращения обруча. Масса обруча m, радиус R, коэффициент трения µ.

 

Задача 17.11

Шайбу раскрутили до угловой скорости и плашмя положили на шероховатый стол. Через какое время вращение шайбы прекратится? Радиус шайбы R. коэффициент трения µ.

 

Задача 17.12

Рис. 17.2 – Каток состоит из сплошного цилиндра и рамы, к которой привязана нить, перекинутая через блок

Каток состоит из сплошного цилиндра массы М = 2,54 кг и рамы, к которой привязана нить, перекинутая через блок (см. рисунок). К концу нити, привязан груз массы m = 0,500 кг. Пренебрегая массой нити, рамы и  блока, найти ускорение катка и натяжение нити.

 

Задача 17.13

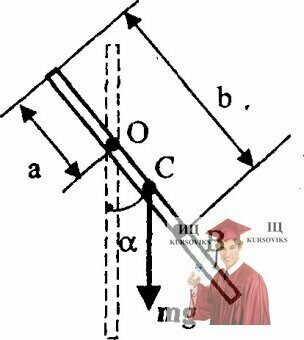
Рис. 17.3 – Тонкий однородный стержень может свободно вращаться вокруг горизонтальной оси

Тонкий однородный стержень длиной L = 1 м может свободно вращаться вокруг горизонтальной оси, проходящей через точку О на стержне (см. рисунок). Стержень отклонили от вертикали на угол α и отпустили. Определить для начального момента времени угловое ε и тангенциальное а_τ, ускорения точки В на стержне. Вычисления произвести для следующих случаев: 1) а = 0, b = 2l/3, α= π/2; 2) а = 1/3, b = l, α =π/3, 3) а = 1/4,b=1/2, α=2π/3.

 

Задача 17.14

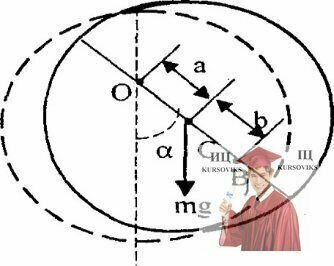
Рис. 17.4 – Однородный диск свободно вращается вокруг горизонтальной оси

Однородный диск радиусом R=10 см может свободно вращаться вокруг горизонтальной оси, перпендикулярной плоскости диска и проходящей через точку О на нем (см. рисунок). Диск отклонили на угол α и отпустили. Определить для начального момента времени угловое ε и тангенциальное а_τ: ускорения точки В, находящейся на диске. Вычисления выполнить для следующих случаев: 1) а = R, b = R/2, α=π/2; 2)a=R/2, b=R/α=π/6; 3) a=2R/3, b=2R/3, α=2π/3

 

Задача 17.15

На горизонтальную ось насажены маховик и легкий шкив радиусом R = 5 см. На шкив намотан шнур, к которому привязан груз массой m = 0,4 кг. Опускаясь равноускоренно, груз прошел путь S= 1,8 время t =3с. Определить момент инерции I маховика. Массу шкива считать пренебрежимо малой.

 

Задача 17.16

Вал массой m = 100 кг и радиусом R = 5 см вращался с частотой n= 8 с^-1. К цилиндрической поверхности вала прижали тормозную колодку с силой F = 40 Н, под действием которой вал остановился через t = 10 с Определить коэффициент трения µ.

 

Задача 17.17

На цилиндр намотана гибкая нерастяжимая лента, масса которой по сравнению с массой цилиндра можно пренебречь. Свободный конец ленты прикрепили к кронштейну и предоставили цилиндру опускаться под действием силы тяжести. Определить линейное ускорение а оси цилиндра, если цилиндр: 1) сплошной; 2) полый тонкостенный.

 

Задача 17.18

Через блок, имеющий форму диска, перекинут шнур. К концам шнура привязали грузики массой m₁ = 100 г и m₂ = 110 г. С каким ускорением а будут двигаться грузики, если масса т блока равна 400 г Трение при вращении блока ничтожно мало.

 

Задача 17.19

Рис. 17.5 – Два тела связаны тонкой нитью, переброшенной через блок

Два тела массами m₁ = 0,25 кг m₂ = 0,15 кг связаны тонкой нитью, переброшенной через блок (см. рисунок). Блок cкреплен на краю горизонтального стола, по поверхности которого скользит тело массой m₁. С каким yскорение a движутся тела и каковы силы Т₁ и Т₂ натяжения нити по обе стороны от блока? Коэффициент трения µ тела о поверхность стола равен 0,2. Масса m блока равна 0,l кг и ее можно считать равномерно распределенной по ободу. Массой нити и трением в подшипниках оси блока пренебречь.

 

Задача 17.20

Через неподвижный блок массой m = 0,2 кг перекинут шнур, к концам которого подвесили грузы массами m₁ = 0,3 кг и m₂= 0,5 кг. Определить силы натяжения T_l и Т₂ шнура по обе стороны блока во время движения грузов, если масса блока равномерно распределена по ободу.

 

Задача 17.21

Шар массой m = 10 кг и радиусом R = 20 см вращается вокруг оси. Проходящей через его центр. Уравнение вращения шара имеет вид φ= А + Bt² + Ct^з, где В = 4 рад/с², С = - 1 рад/с^3. Найти закон изменения момента сил, действующих на шар. Определить момент сил в момент времени t = 2 с.

 

Задача 17.22

Маховик в виде сплошного диска, момент инерции которого I=150 кг•м², вращается с частотой n = 240 об/мин. Через время t =1 мин, как на маховик стал действовать момент сил торможения, он остановился. Определить: 1) момент М сил торможения; 2) число оборотов маховика от начала торможения до полной остановки.

 

Задача 17.23

К ободу однородного сплошного диска радиусом R = 0,5 м приложена постоянная касательная сила F = 100 Н. При вращении диска на него действует момент сил трения М_тр = 2 Нм. Определить массу m диска, если известно, что его угловое ускорение ε постоянно и равно 16 рад/с².

 

Задача 17.24

Частота вращения по маховика. момент инерции I которого равен 120 кг•м², составляет 240 об/мин. После прекращения действия на него вращающегося момента маховик под действием сил трения в подшипниках остановился за время t= π минут. Считая трение в подшипниках постоянным, определить, момент М сил трения.

 

Задача 17.25

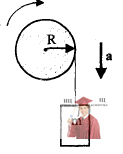
Рис. 17.6 – Однородный сплошной цилиндрический вал

На однородный сплошной цилиндрический вал (см. рисунок) радиусом R = 50 см намотана легкая нить, к концу которой прикреплен груз массой m = 6,4 кг. Груз, разматывая нить, опускается с ускорением а = 2 м/с^2. Определить: 1) момент инерции I вала; 2) массу m₁ вала.

 

Задача 17.26

На однородный сплошной цилиндрический вал радиусом R = 5 см и массой m₁= 10 кг намотана легкая нить, к концу которой прикреплен груз массой m =1 кг (см. рисунок к задаче 17.25). Определить: 1) зависимость S(t), согласно которой движется груз; 2) силу натяжения нити Т; З) зависимость φ(t), согласно которой вращается вал; 4) угловую скорость ω вала через t = 1 с после начала движения; 5) тангенциальное (а_τ) и нормальное (а_n) ускорение точек, находящихся на поверхности вала.

 

Задача 17.27

На однородный сплошной цилиндрический вал радиусом R = 20 см, момент инерции которого I = 0,15 кг•м², намотана легкая нить, к концу которой прикреплен груз массой m= 0,5 кг. До начала вращения барабана высота h груза над полом составляла 2,3 м. Определить: 1) время опускания груза до пола; 2) силу натяжения нити; 3) кинетическую энергию груза в момент удара о пол.

 

Задача 17.28

Через неподвижный блок в виде однородного сплошного цилиндра массой m =0,2 кг перекинута невесомая нить, к концам которой прикреплены тела массами m₁ = 0,35 кг и m₂= 0,55 кг. Пренебрегая трением в оси блока, определить: 1) ускорение грузов: 2) отношение Т₂/Т₁ сил натяжения нити.

С уважением ИЦ "KURSOVIKS"!