Задачи с курса Физика на тему 16, Момент силы, момент импульса. Законы изменения и сохранения момента импульса (32 задачи)
« Назад 47 Задачи с курса Физика на тему 16, Момент силы, момент импульса. Законы изменения и сохранения момента импульса (32 задачи) 10.11.2018 18:38
47 Задачи с курса Физика на тему 16, Момент силы, момент импульса. Законы изменения и сохранения момента импульса (32 задачи) 10.11.2018 18:38Задача 16.1
Тело брошено под углом α= 450 к горизонту с начальной скоростью v0=25 м/с. Масса тела m = 130 г. Найти момент импульса тела L относительно точки бросания: а) в момент, когда тело находится в вершине траектории; б) в момент падения тела на Землю.
Задача 16.2
Найти модуль изменения момента импульса тела относительно точки │ΔL│ при упругом ударе о стенку. Точка О лежит на стенке в плоскости движения тела на расстоянии I от точки удара. Масса тела m, скорость v. Угол между перпендикуляром к стенке и скоростью равен α.
Задача 16.3
Суммарный момент импульса двух материальных точек относительно начала координат О равен L. Чему равен момент импульса этих точек L’ относительно точки O' с радиусом - вектором R? Импульсы точек равны р1, и p2. В каком случае момент импульса системы материальных точек не зависит от положения точки О, относительно которой он берется?
Задача 16.4
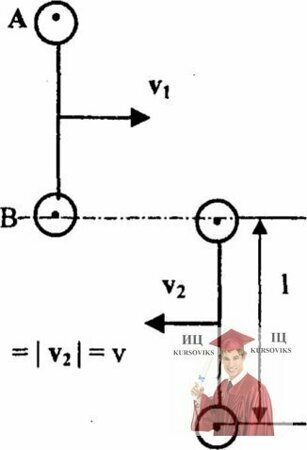
Рис. 16.1 – Две пары шаров жестко соединенные невесомыми стержнями длины
Две пары шаров массы m каждый, жестко соединенные невесомыми стержнями длины (гантели), движутся в плоскости рисунка поступательно навстречу друг другу с одинаковыми скоростями v. В некоторой момент средние шары соударяются. Удар абсолютно упругий. а) Найти момент импульса L., шаров относительно точек А, В, С и произвольной точки D в плоскости удара. б) Как будут двигаться шары после удара? в) Найти угловую скорость вращения гантелей w после удара.
Задача 16.5
Шарик прикреплен к концу легкой нерастяжимой веревки и вращается по окружности радиусом r1= 1,5м с постоянной скоростью 2 м/с. Во время движения шарика веревка укорачивается, при этом период его движения изменяется в 3 раза. Какова новая длина веревки?
Задача 16.6
Найти момент импульса L Земли относительно собственной оси вращения. Плотность Земли р = 5,5* l03 кг/мз, радиус R= 6400 км.
Задача 16.7
Во сколько раз орбитальный момент импульса Луны относительно Земли L больше момента импульса Луны относительно собственной оси Lc. Среднее расстояние между Землей и Луной равно I = 3,84*10 8 м. радиус Луны R = 1.74*106 м.
Задача 16.8
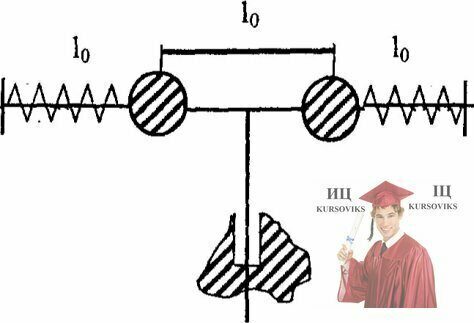
Рис. 16.2 – Шары касаются закрепленных одинаковых пружин длины l0
Два одинаковых маленьких шарика насажены на гладкий горизонтальный стержень, по которому они могут скользить без трения. Шары касаются закрепленных одинаковых пружин длины l0, находящихся в недеформированном состоянии, и соединены нерастяжимой нитью, как показано на рисунке. Всю установку приводят во вращение с постоянной угловой скоростью ω0 и предоставляют самой себе (установка вращается без трения), после чего пережигают нить. Определить угловую скорость вращения после того, как длина каждой пружины стала равной l.
Задача 16.9
Тонкий однородный стержень длиной I = 50 см и массой m = 400 г вращается с угловым ускорением ε=3 рад/с2 около оси, проходящей перпендикулярно стержню через его середину, Определить момент М силы, осуществляющий вращение (вращающий момент).
Задача 16.10
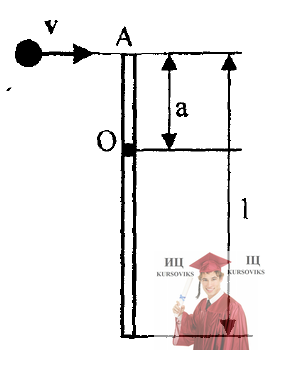
Рис. 16.3 – Однородный тонкий стержень может свободно вращаться вокруг горизонтальной оси z, проходящей через точку О
Однородный тонкий стержень массой m= 0,2 кг и длиной 1 = 1m может свободно вращаться вокруг горизонтальной оси z, проходящей через точку О (см. рисунок). В точку А на стержне попадает пластилиновый шарик, летящий горизонтально (перпендикулярно оси z) со скоростью v =10 м/с и прилипает к стержню. Масса m2 шарика равна 2=10г. Определить угловио скорость о стержня ω линейную скорость u нижнего конца стержня в начальный момент времени. Вычисления выполнить для следующих значений расстояния между точками А и О: 1) l/2;2)1/3; 3)1/4.
Задача 16.11
На краю неподвижной платформы массой m, имеющей форму диска радиусом R, находится человек. С какой угловой скоростью будет вращаться платформа, если человек пойдет по ее краю со скоростью u относительно вертикальной оси, проходящей через его центр масс, относительно платформы. Масса человека m1, момент инерции человека I0 Трением в оси платформы пренебречь.
Задача 16.12
Человек, стоящий на скамье Жуковского, держит в разведенных в стороны руках две гантели массой m = 5 кг каждая. Скамья вращается с частотой v = 1 об/с. Начальное расстояние между гантелями l1=1,4 какой угловой скоростью будет вращаться скамья Жуковского, если человек сблизит гантели до расстояния l2 = 0,4м? Суммарный момент инерции человека и скамьи I0=4 кг•м2 считать постоянным. Как изменится решение задачи, если человек, не сближая гантели, выпустит их из рук?
Задача 16.13
Платформа, имеющая форму однородного диска, вращается по инерции с угловой скоростью ω0. Как будет изменяться со временем угловая скорость платформы, если начнет падать снег? Масса снежинок в единице объема ρ, их скорость u, начальная масса платформы m0, ее радиус R. Считать, что вся выпадающая масса снежинок остается на платформе.
Задача 16.14
Пуля массой m1, летящая горизонтально со скоростью v0, попадает в нижний конец стержня, закрепленного на горизонтальной оси, проходящей через верхний конец стержня, и застревает в нем. Масса стержня m2, длина l. Определить линейную скорость нижнего конца стержня сразу после попадания пули.
Задача 16.15

Рис. 16.4 – Вращения планеты вокруг собственной оси
Найти изменение угловой скорости ∆ω вращения планеты вокруг собственной оси в том случае, когда на ее поверхность упадет метеорит массы m, летящий в плоскости экватора планеты со скоростью v под углом α к вертикали (см. рисунок). Масса планеты М, ее радиус R, угловая скорость ω.
Задача 16.16
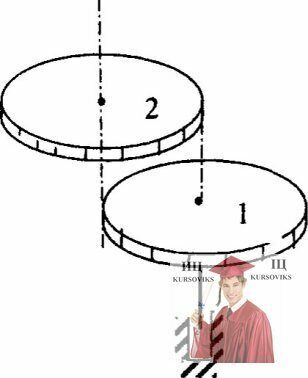
Рис. 16.5 – Два одинаковых однородных диска
Имеются два одинаковых однородных диска. Один из них первоначально неподвижен, но может вращаться без трения вокруг вертикальной фиксированной оси, проходящей через его центр. Второй диск, сообщив ему угловую скорость ω0, роняют в горизонтальном положении на первый диск так, что край одного из дисков совпадает с центром другого. Придя в соприкосновение, диски мгновенно склеиваются. Определить угловую скорость ω, с которой будет вращаться образовавшаяся система.
Задача 16.17
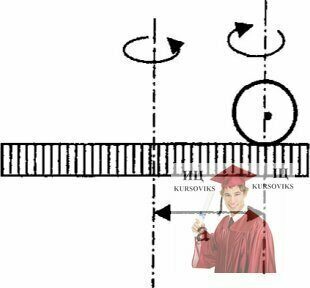
Рис. 16.6 – Расстоянии а от оси вращающегося с угловой скоростью
На каком расстоянии а от оси вращающегося с угловой скоростью ωД диска должен находиться вращающийся в противоположную сторону шарик, чтобы он не изменил своегo положения? ωШ = 5ωД, Мд/Мш- 5, радиусы диска и шарика 10 и 1 км.
Задача 16.18
Металлический стержень массы М = 1,00 кг и длины l=40,0 может вращаться вокруг перпендикулярной к нему оси. проходящей через его центр. В конец стержня попадает пуля массы rn =10,0 г, летящая перпендикулярно к оси и к стержню со скоростью v=200 м/с. Удар пыли о стержень абсолютно упругий. Определить угловую скорость ω. с которой начнет вращаться стержень.
Задача 16.19
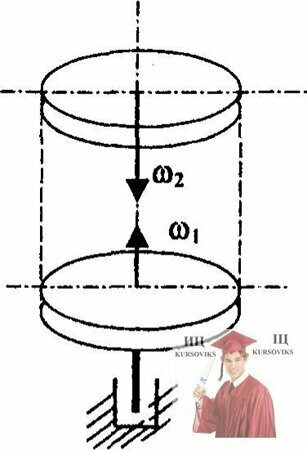
Рис. 16.7 – Слипания двух шероховатых дисков, вращающихся с угловыми скоростями
Определить угловую скорость после «слипания» двух шероховатых дисков, вращающихся с угловыми скоростями ω1 = 20 рад/с и ω2 = 10 рад/с относительно вертикальной оси, совпадающей с осями симметрий дисков (см. рисунок), когда верхний диск упадет на нижний. Масса нижнего диcка rnl = 1 кг, верхнего m2 = 2 кг, радиусы R =0,1м одинаковы.
Задача 16.20
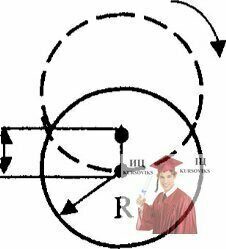
Рис. 16.8 – Диск вращается без трения вокруг перпендикулярной к нему и расположенной горизонтальной оси
Диск радиуса R и массы m может вращаться без трения вокруг перпендикулярной к нему и расположенной горизонтальной оси, отстоящей на расстоянии R/2 от центра диска. Диск начинает вращаться из положения неустойчивого равновесия с нулевой начальной скоростью. Найти момент импульса диска относительно оси вращения в момент прохождения нижнего положения.
Задача 16.21
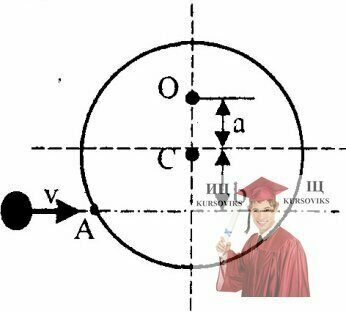
Рис. 16.9 – Однородный диск может свободно вращаться вокруг горизонтальной оси z
Однородный диск массой m1 = 0.2 кг и радиусом R = 20 см может свободно вращаться вокруг горизонтальной оси z перпендикулярной плоскости рисунка и проходящей через точку С(см. рисунок). В точку А на образующей диска попадает пластилиновый шарик. летящий горизонтально (перпендикулярно оси z) со скоростью v = 10.м,с. и прилипает к его поверхности. Масса m2 шарика равна 10 г. Определить угловую скорость о диска и линейную скорость u точки О на диске в начальный момент времени. Вычисления выполнить для следующих значений а и b: 1) а = b =R, 2) а =R/2,b=R; 3) a=2R/3, b=R/2.
Задача 16.22
Человек стоит на скамье Жуковского и ловит рукой мяч массой m = 0,4 кг, летящий в горизонтальном направлении со скоростью v = 20 м/с. Траектория мяча проходит на расстоянии r = 0,8 м от вертикальной оси вращения скамьи. С какой угловой скоростью ω начнет вращаться скамья Жуковского с человеком, поймавшим мяч, если суммарный момент инерции человека и скамьи равен 6 кг•м2?
Задача 16.23
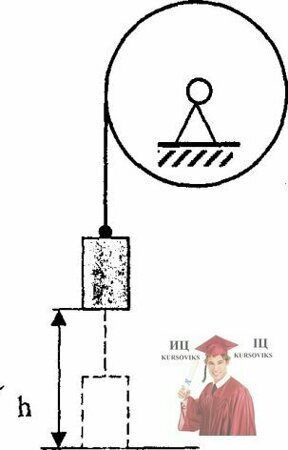
Рис. 16.10 – Маховик, имеющий вид диска к его цилиндрической поверхности прикреплен конец нерастяжимой нити
Маховик, имеющий вид диска радиусом R = 40 см и массой m1= 48 кг, может вращаться вокруг горизонтальной оси. К его цилиндрической поверхности прикреплен конец нерастяжимой нити, к другому концу которой подвешен груз массой m2 = 0,2 кг (см. рисунок). Груз был приподнят и затем отпущен. Упав свободно с высоты h =2 груз натянул нить и благодаря этому привел маховик во вращение. Какую угловую скорость ω груз сообщил при этом маховику?
Задача 16.24
На краю горизонтальной платформы, имеющей формy диска радиусом R = 2м, стоит человек массой m1= 80 кг. Масса m2 платформы равна 240 кг. Платформа может вращаться вокрyг вертикальной оси, проходящей через ее центр. Пренебрегая трением, найти, с какой угловой скоростью ω будет вращаться платформа, если человек будет идти вдоль ее края со скоростью v=2 относительно платформы.
Задача 16.25
Платформа, имеющая форму диска, может вращаться около вертикальной оси. На краю платформы стоит человек массой m1= 60 кг. На какой угол φ повернется платформа, если человек пойдет вдоль края платформы и, обойдя его, вернется в исходную точку на платформе. Масса m2 платформы равна 240 кг. Момент инерции человека рассчитывать как для материальной точки.
Задача 16.26
Платформа в виде диска радиусом R = 1м вращается по инерции с частотой n1 = 6 мин-1. На краю платформы стоит человек, масса которого m = 80 кг. С какой частотой n будет вращаться платформа, если человек перейдет в ее центр? Момент инерции платформы I=120 кг•м 2. Момент инерции человека рассчитывать как для материальной точки.
Задача 16.27
В центре скамьи Жуковского стоит человек и держит в руках стержень длиной l= 2,4 м и массой m = 8 кг, расположенной вертикально по оси вращения скамейки. Скамья с человеком вращается с частотой n1= 1c-l. С какой частотой n2 будет вращаться скамья с человеком, если он повернет стержень в горизонтальное положение? Суммарный момент инерции I человека и скамьи равен 6 кг•м2.
Задача 16.28
Человек стоит на скамье Жуковского и держит в руках стержень, расположенный вертикально вдоль оси вращения скамейки. Стержень служит осью вращения колеса, расположенного на верхнем конце стержня. Скамья неподвижна, колесо вращается с частотой n1= 10 с- 1. Радиус R колеса равен 20 см. его масса m = 3 кг. Определить частоту вращения n2 скамьи. если человек повернет стержень на угол 1800 Суммарный момент инерции человека и скамьи равен 6 кг•м.
Задача 16.29
Горизонтальная платформа массой m = 25 кг и радиусом R = 0.8 м вращается с частотой n1=18 мин-1. В центре стоит человек и держит на расставленных рyках гири. Считая платформy диском. определить частоту вращения платформы. если человек, опустив руки. уменьшит свой момент инерции от I1= 3.5 кг•*м2 до I2=1 кг•м2.
Задача 16.30
Человек, стоящий на скамье Жуковского, держит в руках стержень длиной l = 2, 5 м и массой m= 8 кг, расположенный вертикально вдоль оси вращения скамейки. Эта система (скамья и человек) обладает моментом инерции I=10 кг•м2 и вращается с частотой n1=12мин-1. Определить частоту n2 вращения системы, если стержень повернуть в горизонтальное положение.
Задача 16.31
Человек массой m = 60 кг, стоящий на краю горизонтальной платформы массой М = 120 кг, вращающейся по инерции вокруг неподвижной вертикальной оси с частотой n1=10 мин-1, переходит к центру. Считая платформу круглым однородным диском, а человека — точечной массой, определить, с какой частотой n2 будет вращаться платформа.
Задача 16.32
Платформа, имеющая форму сплошного однородного диска, может вращаться по инерции вокруг неподвижной вертикальной оси. На краю платформы стоит человек, масса которого в 3 раза меньше массы платформы. Определить, как и во сколько раз изменится угловая скорость вращения платформы, если человек перейдет ближе к центру на расстояние, равное половине радиуса платформы.
С уважением ИЦ "KURSOVIKS"!