Задачи с курса Физика на тему 15, Момент инерции (31 задача)
« Назад 46 Задачи с курса Физика на тему 15, Момент инерции (31 задача) 09.11.2018 22:02
46 Задачи с курса Физика на тему 15, Момент инерции (31 задача) 09.11.2018 22:02Задача 15.1
Определить момент инерции l материальной точки массой m = 0,3 кг относительно оси, отстающей от точки на r = 20 см.
Задача 15.2
Два маленьких шарика массой m = l0 г каждый скреплены тонким невесомым стержнем длиной l= 20 см. Определить момент инерции системы относительно оси, перпендикулярной стержню и проходящей через центр масс.
Задача 15.3

Рис. 15.1 - Два шарика закреплены на тонком невесомом стержне
Два шарика массами m и 2m (m =10 г) закреплены на тонком невесомом стержне длиной l = 40 см так, как это указано на рисунке (см.а, б). Определить момент инерции системы относительно оси, перпендикулярной стержню и проходящей через его конец в этих двух случаях. Размерами шаров пренебречь.
Задача 15.4
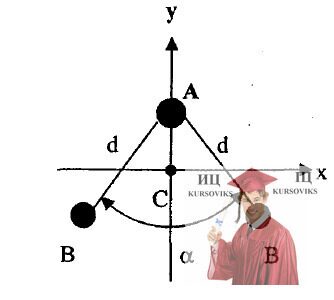
Рис. 15.2 – Система координат инерции
Определить моменты инерции Ix, Iy, Iz трехатомных молекул типа АВ2 относительно осей х, у, z проходящих через центр инерции С молекулы ( ось z перпендикулярна плоскости ху). Межъядерное расстояние АВ обозначено d, валентный угол α. Вычисления выполнить для следующих молекул: Н2O (d = 0,97 нм, α= 104030'); 2) SO2(d = 0,145 нм, α= 1240).
Задача 15.5
Три маленьких шарика массой m= 10 г каждый расположены в вершинах равностороннего треугольника со стороной а 20 см и скреплены между собой. Определить момент инерции I системы относительно оси: 1) перпендикулярной плоскости треугольника и проходящей через центр описанной окружности; 2) лежащей в плоскости треугольника и проходящей через центр описанной окружности и одну из вершин треугольника. Массой стержней, соединяющих шары, пренебречь.
Задача 15.6
Определить момент инерции I тонкого однородного стержня длиной l=30 см и массой m = 100 г относительно оси, перпендикулярной стержню и проходящей через: 1) его конец; 2) его середину; 3) точку, отстоявшую от конца стержня на 1/3 его длины.
Задача 15.7
Определить момент инерции тонкого однородного стержня длиной l = 60 см и массой m= 100 г относительно оси, перпендикулярной ему и проходящей через точку стержня, удаленную на а = 20 см от одного из его концов.
Задача 15.8
Вычислить момент инерции проволочного прямоугольника со стороной а = 12 см и b = 16 см относительно оси, лежащей в плоскости прямоугольника и проходящей через середины малых сторон. Масса равномерно распределена по длине проволоки с линейной плотностью τ= 0,1 кг/м.
Задача 15.9

Рис. 15.3 – Два однородных тонких стержня АВ скреплены под прямым углом
Два однородных тонких стержня АВ длиной l1=40 см и массой m1 = 900 г и СD) длиной l2 = 40 см и массой m2 = 400 г скреплены под прямым углом (см. рисунок). Определить момент инерции системы стержней относительно оси 00', проходящий через конец стержня АВ параллельно стержню CD.
Задача 15.10
Решить задачу 15.9 для случая, когда ось OO’ проходит через точку А перпендикулярно плоскости чертежа.
Задача 15.11
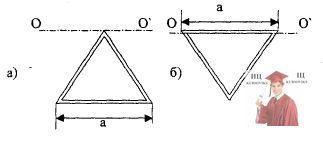
Рис. 15.4 – Момент инерции проволочного равностороннего треугольника
Определить момент инерции проволочного равностороннего треугольника со стороной а=10 см относительно: 1) оси, лежащей в плоскости треугольника и проходящей через его вершину параллельно стороне, противоположной этой вершине (рис. а); 2) оси, совпадающей с одной из сторон треугольника (рис. б). Масса m треугольника равна 12 г и равномерно распределена по длине проволоки.
Задача 15.12

Рис. 15.5 – На концах тонкого однородного стержня прикреплены маленькие шарики
На концах тонкого однородного стержня длиной 1 и массой 3m прикреплены маленькие шарики массами m и 2m. Определить момент инерции I такой системы относительно оси, перпендикулярной стержню и проходящей через точку О, лежащую на оси стержня. Вычисления выполнить для случаев а, б, в, г, д, изображенных на рисунке. При расчете принять l= 1 м, m = 0,l кг. Шарики рассматривать как материальные точки.
Задача 15.13
Найти момент инерции I однородного кольца радиусом R = 20 см и массой m = 100 г относительно оси, лежащей в плоскости кольца и проходящей через его центр.
Задача 15.14
Определить момент инерции I кольца массой m = 50 г и радиусом R = 10 см относительно оси, касательной к кольцу.
Задача 15.15
Вывести формулу для момента инерции полого шара относительно оси, проходящей через его центр. Масса шара равна т, внутренний радиус — r, внешний R.
Задача 15.16
Вывести формулу для момента инерции цилиндрической мирты относительно оси, совпадающей с ее осью симметрии. Масса муфты равна m внутренний радиус —r, внешний R.
Задача 15.17
Определить момент инерции I сплошного однородного диска радиусом R = 40 см и массой m= 1 кг относительно оси, проходящей через середину одного из радиусов- перпендикулярно плоскости диска.
Задача 15.18

Рис. 15.6 – В однородном диске радиусом вырезано круглое отверстие центр которого находится на расстоянии от оси диска
В однородном диске массой m = 1кг и радиусом r =30 см вырезано круглое отверстие диаметром d= 20 см, центр которого находится на расстоянии I = l5 см от оси диска (см. рисунок). Найти момент инерции полученного тела относительно оси, проходящей перпендикулярно плоскости диска через его центр.
Задача 15.19
Найти момент инерции I плоской однородной прямоугольной пластины массой m= 800 г относительно оси, совпадающей с одной из ее сторон, если длина а другой стороны равны 40 см.
Задача 15.20
Определить момент инерции тонкой плоской пластины со сторонами а =10 см и b = 20 см относительно оси, проходящей через центр масс пластины параллельно большей стороне. Масса пластины равномерно распределена по ее площади с поверхностной плотностью σ = 1,2кг/м2
Задача 15.21
В тонком диске массой m и радиусом R вырезано n круглых отверстий радиусами r на равных расстояниях а от центра диска. Определить момент инерции диска относительно оси, проходящей через его центр масс.
Задача 15.22
Определить момент инерции цилиндрической муфты относительно оси, совпадающей с ее осью симметрии. Масса муфты m=2 внутренний радиус r =0,03 м, внешний R =0,05 м.
Задача 15.23
Цилиндр диаметром 12 см, имеющий массу 3 кг, лежит боковой поверхностью на горизонтальной плоскости. Определить момент инерции цилиндра относительно оси, проходящей по линии контакта с плоскостью.
Задача 15.24
Определить момент инерции полого шара массой m = 0,5 кг относительно касательной. Внешний радиус шара R = 0,02 м; внутренний r= 0,01 м.
Задача 15.25
Найти момент инерции тонкой сферической оболочки относительно оси симметрии. Масса сферы m радиус сферы R.
Задача 15.26

Рис. 15.7 – Момент инерции однородного стержня, вращающегося вокруг оси, проходящей через один из его концов
Найти момент инерции однородного стержня, вращающегося вокруг оси, проходящей через один из его концов (см. рисунок). Ось вращения составляет угол со стержнем. Длина стержня l, масса m.
Задача 15.27
Найти момент инерции тонкого однородного стержня с прикрепленными на его концах одинаковыми сосредоточенными грузами массами rn1 и m2. Масса стержня m, его длина l. Ось вращения перпендикулярна стержню и проходит через его центр.
Задача 15.28
Длины сторон однородного прямоугольного параллелепипеда равны а, b, с. Масса тела m. Определить момент инерции этого тела относительно оси, проходящей через его центр перпендикулярно плоскости, в которой лежат стороны параллелепипеда длиной а и b.
Задача 15.29
Диск способен вращаться относительно оси, проходящей через его крайнюю точку и лежащую в плоскости диска. Считая массу m и радиус диска R заданными, найти его момент инерции.
Задача 15.30
Определить момент инерции шара массой m, радиусом R, считая, что в нем имеется полость радиусом r. Центры полости и шара отстоят на расстояние а друг от друга. Ось вращения проходит через эти центры.
Задача 15.31
Найти момент инерции тонкой однородной прямоугольной пластинки относительно оси, проходящей перпендикулярно к плоскости пластинки через одну из ее вершин. Стороны пластинки а и b, масса m.
С уважением ИЦ "KURSOVIKS"!














