44 Задачи с курса Физика на тему 13, Совместное применение законов сохранения импульса и энергии (80 задач) 09.11.2018 21:49

Задача 13.1

Человек стоит на неподвижной тележке и бросает горизонтально камень массой m = 8,0 кг со скоростью v = 5,0 м/с. Определить, какую при этом человек совершает работу, если масса тележки вместе с человеком М = 160 кг. Проанализируйте зависимость работы от массы М.

 

Задача 13.2

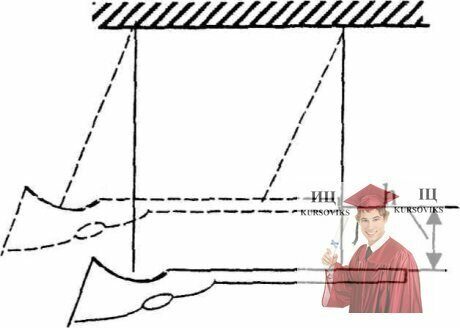
Рис. 13.1 - Винтовка в результате отдачи

Винтовка массой М =2,8 кг подвешена горизонтально на двух параллельных нитях. При выстреле в результате отдачи она откачнулась вверх на h = 19,6 см (см. рисунок). Определить скорость, с которой вылетела пуля. Масса пули m = 9,8 г,

 

Задача 13.3

На тележку массой М, движущуюся со скоростью v, опускают с небольшой высоты кирпич массой m. Найти изменение внутренней энергии тележки.

 

Задача 13.4

Два шара массами m₁=1кг и m₂=2 кг движутся поступательно вдоль горизонтальной прямой в одном направлении со скоростями v₁=7,0 м/с и v₂= 1м/с. Определить скорость шаров после абсолютно упругого удара,

 

Задача 13.5

Шарик массой m₁, двигавшийся поступательно со скоростью v_l, налетает на неподвижный шарик массой m₂. Определить скорость шариков после абсолютно упругого центрального удара. Проанализировать зависимости скоростей шариков от соотношения масс. Показать, что в случае абсолютно упругого удара о массивное тело направление скорости шарика меняется на обратное.

 

Задача 13.6

Легкий шарик начинает свободно падать и, пролетев расстояние L сталкивается упруго с тяжелой плитой, движущейся вверх со скоростью u. На какую высоту подпрыгнет шарик после удара?

 

Задача 13.7

Тело после абсолютно неупругого удара о неподвижное тело стало двигаться в n=4 раза медленнее. Определить долю энергии, перешедшей во внутреннюю энергию тела.

 

Задача 13.8

Два шарика массами m₁ и m₂ подвешены на нитях одинаковой длины так, что они соприкасаются. Один шарик отводят в плоскости нитей на угол α и отпускают. Происходит центральный удар шариков. На какие углы α₁ и α₂ относительно отвесной линии отклонятся шарики после удара (углы считать малыми, удар - упругим)?

 

Задача 13.9

На какой угол β отклонятся шарики (см. задачу 13.8), если удар неупругий?

 

Задача 13.10

Два идеально упругих шарика массами m₁ и m₂ движутся вдоль одной и той же прямой со скоростями v₁ и v₂. Во время столкновения шарики начинают деформироваться и часть кинетической энергии переходит в потенциальную энергию - деформации. Затем деформация уменьшается и запасенная потенциальная энергия вновь переходит в кинетическую. Найти максимальное значение энергии деформации.

 

Задача 13.11

Деревянный шар массой М лежит на штативе, верхняя часть которого выполнена в виде кольца. Снизу в шар попадает пуля, летящая вертикально, и пробивает его. При этом шар поднимается на высоту h. На какую высоту поднимется пуля над штативом, если ее скорость перед ударом о шар была v?

 

Задача 13.12

Тело массы m,, движущееся со скоростью v, налетает на покоящееся тело и после упругого соударения отскакивает от него под yглом 90° к первоначальном направлению своего движения со скоростью v_2. Определить маccу второго тела.

 

Задача 13.13

Рис. 13.2 - Три шара с одинаковыми радиусами подвешены рядом на нитях

Три шара с одинаковыми радиусами, но различными массами подвешены рядом на нитях одинаковой длины и соприкасаются. Шар массы m₁ отклоняется так, что он поднимается на высоту Н, и отпускают (см. рисунок). При каких массах m₂ и m₃ все три шара после соударения первого шара со вторым и второго с третьим будут иметь одинаковые импульсы? На какую высоту они поднимутся? Все соударения считать абсолютно упругими.

 

Задача 13.14

Рис. 13.3 - На пути тела, скользящего по гладкому горизонтальному столу, находится незакрепленная горка

На пути тела, скользящего по гладкому горизонтальному столу, находится незакрепленная горка высоты Н = 2 м (см. рисунок). При какой минимальной скорости тело сможет преодолеть горку? Масса горки в пять раз больше массы тела. Считать, что тело движется не  отрываясь от горки. Тело по горке, а также горка по столу скользят без трения.

 

Задача 13.15

Рис. 13.4 - Профиль железнодорожной горки, используемой на сортировочной станции

Профиль железнодорожной горки, используемой на сортировочной станции, показан на рисунке. На горизонтальном участке на расстоянии L от конца уклона стоит вагон 1. С горки скатывается без начальной скорости вагон 2, а через время t вагон З. На каком расстоянии от конца уклона все три вагона окажутся сцепленными? Вагоны одинаковы и снабжены автосцепкой. Трением пренебречь. Высота горки равна Н.

 

Задача 13.16

Рис. 13.4 - Тело массы подвешено на длинном легком стержне

Тело массы М подвешено на длинном легком стержне длины 1, закрепленном в точке О (см. рисунок). В тело попадает летящая горизонтально пуля массы m(m<<М), в результате чего стержень отклоняется на угол α.Найти первоначальную кинетическую энергию Е_к пули для трех случаев: а) пуля после удара застревает в теле; б) горизонтальная скорость пули после удара равна нулю; в) пуля отскакивает назад со скоростью v' Массой стержня пренебречь.

 

Задача 13.17

В покоящийся шар 1 массы m упруго ударяется шар 2 массы m/2. После удара шар 2 движется в направлении, перпендикулярном к первоначальному. Под каким углом α к первоначальному направлению движения шара 2 будет двигаться после удара шара1?

 

Задача 13.18

Движущийся шар массы m упруго ударяется в шар массы М, который покоится. После удара шар массы m движется в направлении, противоположном первоначальному. Во сколько раз изменилась энергия шара массы m?

 

Задача 13.19

Рис. 13.5 - Брусок массой М касается недеформированной пружины прикрепленной к стене

Брусок массой М касается недеформированной пружины длины l₀ прикрепленной к стене, как показано на рисунке. В брусок попадает пуля массой m, летевшая с горизонтальной скоростью v₀. Определить жесткость пружины k, если в момент максимального сжатия ее длина составила 1. Коэффициент трения бруска о поверхность равен μ. Чему равно также количество выделившегося тепла?

 

Задача 13.20

Два одинаковых шара массой m = 0,3 кг подвешены на нитях длиной l = 1 м так, что они касаются друг друга. Один из шаров отклонили на угол α = 10⁰ и отпустили. Считая удар абсолютно упругим, определить время соударения шаров, если средняя сила удара F = 500 Н.

 

Задача 13.21

Снаряд массой m₁, летящий горизонтально вдоль рельс, попадает в вагонетку с песком массой m₂, которая первоначально покоилась. Найти наименьшую скорость снаряда, при которой он может выйти через противоположную стенку вагонетки, если средняя сила трения его о песок равна F, а длина вагонетки 1. Трением колес о рельсы пренебречь, стенки вагонетки считать тонкими, не оказывающими существенного сопротивления движению.

 

Задача 13.22

Рис. 13.6 - Два одинаковых шара покоятся на гладкой горизонтальной плоскости

Два одинаковых шара массой m₁ каждый покоятся на гладкой горизонтальной плоскости, касаясь друг друга. Третий шар налетает на них, двигаясь по прямой) касающейся обоих шаров (см. рисунок). Найти массу налегающего шара m₂, если после удара он остановился. Радиусы всех шаров одинаковы, удар считать абсолютно упругим.

 

Задача 13.23

На шероховатой горизонтальной плоскости лежит два кубика массой m₁ и m₂, между которыми находится сжатая пружина. Потенциальная энергия сжатой пружины равна Е_n. В некоторый момент пружина мгновенно распрямляется и сообщает кубикам некоторые скорости. На сколько увеличится расстояние между кубиками после их остановки по сравнению с первоначальным? Каковы начальные скорости кубиков? Коэффициент трения равен μ.

 

Задача 13.24

Груз копра массой m, падает на сваю массой m₂ с высоты Н без начальной скорости. Предполагая, что удар между сваей и грузом абсолютно неизрмгий, найти глубину погружения сваи в грунт, если средняя сила сопротивления со стороны грунта равна F. Клин массой m₁ находится на гладкой горизонтальной поверхности. На наклонной плоскости клина на высоте Н лежит брусок массой m₂, который может скользить по клину без трения. Наклонная плоскость клина имеет плавный переход к горизонтальной плоскости. В начальный момент система покоится. Определить скорость клина и бруска в тот момент, когда брусок соскальзывает на горизонтальную плоскость.

 

Задача 13.26

Пуля массой m₁ попадает в деревянный брусок массой m₂, подвешенной на нити длиной l. С какой минимальной скоростью должна лететь пуля, чтобы после абсолютно неупругого взаимодействия брусок описал окружность?

 

Задача 13.27

Легкий шар начинает свободно падать и, пролетев расстояние S, сталкивается упруго с тяжелой плитой, движущейся вверх со скоростью и. На какую высоту h относительно положения плиты в момент удара подскочит шарик после удара?

 

Задача 13.28

На гладкой горизонтальной поверхности на расстоянии l=3 вертикальной стенки находится шар массой М. Другой шар массой m скользит с некоторой скоростью по направлению от стенки к шару М. После абсолютно упругого удара шаров шар m достигает стенки и, упруго отразившись от нее, догоняет шар М. Определить, на каком расстоянии от стенки произошло второе соударение шаров, если M/m = n= 5.

 

Задача 13.29

Шар массой m₁ = 1 кг движется со скоростью v₁=4 м/с и сталкивается с шаром массой m₂ = 2 кг, движущимся навстречу ему со скоростью v₂ = 3 м/с. Найти скорости шаров после удара. Удар считать упругим, центральным.

 

Задача 13.30

Шар массой m, движущийся со скоростью v, ударяется о неподвижный шар массой М. Происходит абсолютно упругий центральный удар. Определить, при каком соотношении масс M/m налетающий шар теряет максимальную часть своей кинетической энергии. Найти это значение энергии.

 

Задача 13.31

Происходит соударение двух абсолютно упругих шаров, движущихся вдоль одной прямой навстречу друг другу, массы которых равны m₁ и m₂. Начальные скорости шаров v₁ и v₂. Удар центральный. Определить максимальную энергию упругой деформации.

 

Задача 13.32

Шар абсолютно упруго сталкивается с таким же, но покоящимся шаром. Под каким углом они разлетятся? Удар нецентральный.

 

Задача 13.33

Рис. 13.7 - Две ступеньки одинаковой высоты находятся на расстоянии одна за другой

Две ступеньки одинаковой высоты h находятся на расстоянии l одна за другой (см. рисунок). На краю одной ступеньки лежит маленький шарик. Тело, масса которого много больше массы шарика, налетает на шарик, соударяется с ним и сталкивает его со ступеньки. Какую скорость перед соударением с шариком должно иметь тело, чтобы шарик после одного подскока от горизонтальной плоскости попал на вторую ступеньку? Все соударения абсолютно упругие.

 

Задача 13.34

На два одинаковых неподвижных шара налетает такой же третий, центр которого движется по средней линии отрезка, соединяющего центры неподвижных шаров. После упругого удара налетающий шар останавливается. Каково расстояние между центрами первоначально неподвижных шаров. если шаров R?

 

Задача 13.35

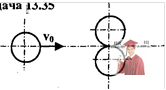
Рис. 13.8 – Шайбы вид сверху

На гладкой горизонтальной поверхности находятся две одинаковые соприкасающиеся шайбы. Третья такая же шайба налетает на них со скоростью v₀ =5 м/с, направленной по общей касательной к покоящимся шайбам (см. рисунок: вид сверху). После столкновения налетающая шайба движется вдоль первоначального направления со скоростью v= 2 м/с. Какое количество теплоты Q выделилось при столкновении? Масса каждой шайбы m = 100 г.

 

Задача 13.36

Шар абсолютно неупруго соударяется с другим таким же, но неподвижным шаром. Какая доля энергии переходит в тепло?

 

Задача 13,37

Тележка с песком, общей массой М, свободно катится по горизонтальным рельсам со скоростью v₀. Камень массой m, брошенный горизонтально со скоростью v вдогонку тележке, попадает в нее и застревает в песке. Определить скорость u тележки после попадания камня и количество тепла Q, выделившегося при этом. Считать, что камень брошен с близкого расстояния.

 

Задача 13.38

На покоящуюся частицу массой m_l налетает частица массой m₂. После соударения одна из частиц полетела под прямым углом, а другая — под углом α = 30⁰ к направлению первоначальной скорости налетевшей частицы. Найти отношение масс m₂ /m₁ если при столкновении η = 20 % первоначальной энергии перешло в тепло.

 

Задача 13.39

Рис. 13.9 – Небольшая шайба массой соскальзывает с гладкой горки и попадает на доску

Небольшая шайба массой m без начальной скорости соскальзывает с гладкой горки высотой h и попадает на доску М, лежащую на горизонтальной гладкой плоскости (см. рисунок). Вследствие трения между шайбой и доской шайба тормозится и, начиная с некоторого момента, движется вместе с доской как единое целое. Найти суммарную работу сил трения в этом процессе.

 

Задача 13.40

Телу массой m = 1 кг, лежащему на длинной тележке, сообщили скорость v= 10 см/с, направленную вдоль тележки. Коэффициент трения между телом и поверхностью тележки равен μ = 0,2. Масса тележки М = 100 кг. Тележка может перемещаться по рельсам без трения. Найти перемещение Δr тела относительно тележки и путь S, пройденный тележкой к моменту, когда тело на ней остановится.

 

Задача 13.41

Используя условия задачи 13.40, найти перемещение тела относительно тележки, если коэффициент трения меняется по закону μ=αх, где α=0,1 м^-1, а х - путь, пройденный телом по тележке, отсчитываемый от координаты начала движения.

 

Задача 13.42

На стоящий на горизонтальном полу клин массой М с высоты h падает шар массой m и отскакивает в горизонтальном направлении. Найти горизонтальную скорость клина после удара. Трением и сопротивлением воздуха пренебречь. Удар шара о клин считать абсолютно упругим.

 

Задача 13.43

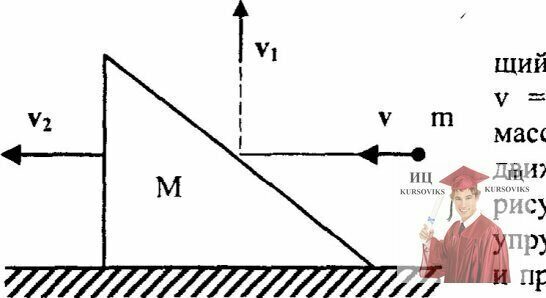
Рис. 13.10 – Шарик летящий горизонтально ударяется в призму после удара движется вертикально вверх

Шарик массой m = 18 г, летящий горизонтально со скоростью v=10 м/с, ударяется в призму массой М=50 г и после удара движется вертикально вверх (см. рисунок). Считая удар абсолютно упругим, найти скорости шарика и v₁ призмы v₂ после удара. Трением призмы о горизонтальную поверхность пренебречь.

 

Задача 13.43

Рис. 13.11 – горизонтальной плоскости лежит клин падает шарик и отскакивает под углом α к горизонту

На горизонтальной плоскости лежит клин массой М. С высоты Н свободно падает шарик массой m, упруго ударяется о поверхность клина и отскакивает под углом α к горизонту (см. рисунок). На какую максимальную высоту относительно точки удара о клин поднимется шарик? Трением клина о плоскость и сопротивлением воздуха пренебречь.

 

Задача 13.45

Рис. 13.12 – горизонтальной плоскости лежит клин падает шарик и отскакивает под углом α

На горизонтальной плоскости лежит клин с углом при основании α < 45 ⁰, масса которого равна М. Небольшой шарик массой m <<М упруго ударяется о наклонную плоскость клина и отскакивает под углом α к ней (см. рисунок). На какую максимальную высоту относительно точки удара о клин поднимется шарик, если в момент удара он имел скорость v_о, направленную горизонтально? Трением клина о плоскость и сопротивлением воздуха пренебречь.

 

Задача 13.46

Рис. 13.13 – Гладка горизонтальна плоскость находится тело массой М и на нем небольшая шайба массой m

На гладкой горизонтальной плоскости находится тело массой М и на нем небольшая шайба массой m. Шайбе сообщили скорость v₀. На какую высоту h_max (по сравнению с первоначальным уровнем ) она поднимется после отрыва от тела М? Трением пренебречь.

 

Задача 13.47

Пуля массой m, имеющая скорость м, летит горизонтально и пробивает подвешенное на тонкой нити длиной l тело массой М, в результате чего скорость пули уменьшается вдвое. Какая часть кинетической энергии пули ушла на нагревание? На какой угол отклонилось тело после удара?

 

Задача 13.48

В неподвижный шар массой М = 1,6 кг, подвешенный на невесомой нерастяжимой нити длиной l=80 см, попадает пуля массой m = 10 г и застревает в нем. При этом шар отклоняется на угол α = 30⁰. С какой скоростью летела пуля, если вектор скорости был направлен под углом β = 60⁰ к горизонту?

 

Задача 13.49

На легком стержне длиной l висит деревянный шар массой М. В шар попадает пуля массой m, имеющая в момент удара скорость v, направленную под углом α к горизонту. На какой угол β отклонится стержень после неупругого центрального удара пули, если она застревает в шаре?

 

Задача 13.50

Рис. 13.14 – Пуля летевшая горизонтально попадает в висящее на двух канатах бревно

Пуля массой m, летевшая горизонтально со скоростью v, попадает в висящее на двух канатах бревно (см. рисунок). Определить угол α отклонения канатов от вертикали и количество выделившегося тепла Q при застревании пули. Масса пули m = 10 г, масса бревна М = 10 кг, длина каната l = 1 м, скорость пули в момент удара v= 700 м/с.

 

Задача 13.51

Пуля массой m, имеющая начальную скорость v_o, пробивает подвешенный на нити груз такой же массы m и застревает во втором таком же грузе, подвешенном на некотором расстоянии от первого. Найти количество выделившейся в первом грузе теплоты, если во втором грузе выделилось Q₂ теплоты. Временем взаимодействия пули с грузами пренебречь.

 

Задача 13.52

Рис. 13.15 – Два маятника в виде шаров разных масс свободно подвешены на нитях разной длины

Два маятника в виде шаров разных масс m₁ и m₂ свободно подвешены на нитях разной длины l₁и l₂ так, что шары соприкасаются (см. рисунок). Первый шарик отводят в плоскости нитей на угол B от первоначального положения и отпускают. На какие углы α₁ и α₂ отклоняют шарики после центрального упругого удара?

 

Задача 13.53

С высоты h без начальной скорости падает шар массой М. На высоте h/2 в шар попадает пуля массой m << М, имевшая в момент удара скорость v, направленную вниз под углом α к горизонту, и застревает в нем. Определить, с какой скоростью u шар упадет на Землю. Сопротивлением воздуха пренебречь.

 

Задача 13.54

Рис. 13.16 – На гладкой горизонтальной поверхности находится брусок, на котором укреплен штатив

На гладкой горизонтальной поверхности находится брусок, на котором укреплен штатив (см. рисунок). К штативу привязан на невесомой нерастяжимой нити шарик. Сначала нить с шариком удерживают под углом α₀= 60 к вертикали, потом отпускают. Найти максимальную скорость бруска. Масса шарика m = 300 г, масса бруска со штативом М =1 кг, длина нити l = 20 см.

 

Задача 13.55

Рис. 13.17 – Шарик поднимают вертикально на высоту h = 30 см и отпускают

Шарик массой m = 0,1кг закреплен на полу двумя одинаковыми пружинами жесткостью k=15 H/м каждая. В исходном состоянии пружины не деформированы и имеют длину l = 40 см. Шарик поднимают вертикально на высоту h = 30 см и отпускают (см. рисунок). Какой импульс передает шарик полу при абсолютно упругом ударе?

 

Задача 13.56

Рис. 13.18 – Тела массами связаны недеформированной пружиной жесткостью

Тела массами m₁ и m₂ связаны недеформированной пружиной жесткостью k (см. рисунок). Определить наименьшую скорость, которую необходимо сообщить телу массой m₁, чтобы пружина сжалась на величину ∆x. Трения нет.

 

Задачу 13.57

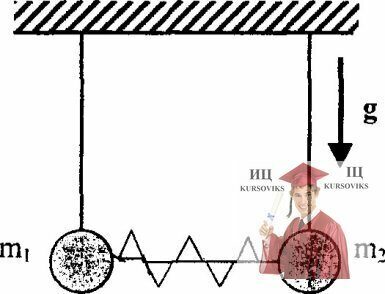
Рис. 13.19 – Шарики висят на длинных одинаковых нитях между ними находится сжатая пружина

Два шарика массой m₁ и m₂ висят на длинных одинаковых нитях. Между ними находится сжатая пружина, которая удерживается в сжатом состоянии связывающей ее нитью (см. рисунок). Потенциальная энергия деформированной пружины равна Е. Нить, связывающую пружину, пережигают. Найти максимальную высоту, на которую поднимутся шарики.

 

Задачу 13.58

Рис. 13.20 – В баллистический маятник попала пуля и застряла в нем

В баллистический маятник массой М = 5 кг попала пуля массой m= 10 г и застряла в нем. Найти скорость v пули, если маятник, отклонившись после удара, поднялся на высоту h=10 см.

 

Задача 13.59

Два груза массами m₁= 10 кг и m₂ = 15 кг подвешены на нитях длиной l= 2 м так, что грузы соприкасаются между собой. Меньший груз был отклонен на угол φ = 60⁰ и выпущен. Определить высоту h, на которую поднимутся оба груза после удара. Удар грузов считать неупругим.

 

Задача 13.60

Два неупругих шара массами m₁ = 2 кг и m₂ = 3 кг движутся со скоростями соответственно v₁ = 8 м/с и v₂= 4 м/с. Определить увеличение ∆U внутренней энергии шаров при их столкновении в двух случаях: 1) меньший шар нагоняет больший; 2) шары движутся навстречу друг другу.

 

Задача 13.61

Шар массой m₁, летящий со скоростью v₁=5 м/с, ударяет неподвижный шар массой m₂. Удар прямой, неупругий. Определить скорость u шаров после удара, а также долю w кинетической энергии летящего шара, израсходованную на увеличение внутренней энергии этих шаров. Рассмотреть два случая: 1)m₁= 2 кг; m₂ = 8 кг; 2) m₁ = 8 кг; m₂ = 2 кг.

 

Задача 13.62

Шар массой m₁ = 2 кг налетает на покоящийся шар массой m₂ = 8 кг. Импульс р₁, движущегося шара равен 10 кг•м/с. Удар шаров упругий. Определить непосредственно после удара: 1) импульсы p₁ первого шара и р₂ второго шара; 2) изменение импульса ∆p₁ первого шара; З) кинетические энергии Т`<sub>1</sub> первого шара и Т`₂ второго шара; 4) изменение ∆Т₁, кинетической энергии первого шара; 5) долю w кинетической энергии, переданной первым шаром второму.

 

Задача 13.63

Шар массой m₁ = 6 кг налетает на другой покоящийся шар массой m₂ = 4 кг. Импульс р₁ первого шара равен 5 кг•м/с. Удар шаров прямой, неупругий. Определить непосредственно после удара: 1) импульсы p₁ первого шара и p₂ второго шара; 2) изменение ∆р₁: импульса первого шара; 3) кинетические энергии Т`<sub>1</sub> первого шара и Т`₂ второго шара; 4) изменение ∆Т: кинетической энергии первого шара; 5) долю w₁ кинетической энергии, переданной первым шаром второму и долю w₂ кинетической энергии, оставшейся у первого шара; 6) изменение ∆U внутренней энергии шаров; 7) долю w кинетической энергии первого шара, перешедшей во внутреннюю энергию шаров.

 

Задача 13.64

Шар массой m₁ = 200 г, движущийся со скоростью v₁= 10 м/с, удaряет неподвижный шар массой m₂ = 800 г. Удар прямой, абсолютно упругий. Каковы будут скорости u₁ и u₂ шаров после удара?

 

Задача 13.65

Шар массой m = 1,8 кг сталкивается с покоящимся шаром большей массы М. В результате прямого упругого удара шар потерял w= 0,36 своей кинетической энергии. Определить массу большого шара.

 

Задача 13.66

Из двух соударяющихся абсолютно упругих шаров больший шар покоится. В результате прямого удара меньший шар потерял w = 3/4 своей кинетической энергии. Определить отношение к = М/m масс шаров.

 

Задача 13.67

Определить максимальную часть кинетической энергии w, которую может передать частица массой m₁= 2•*10^-22 г, сталкиваясь упруго с частицей массой m₂ = 6*10^-22 г, которая до столкновения покоилась.

 

Задача 13.68

Частица массой m₁=10^-25 кг обладает импульсом р₁= 5*10-²⁰ кг•м/с., Определить, какой максимальный импульс p₂ может передать эта частица, сталкиваясь упруго с частицей массой m₂ = 4•10 -²⁵ кг, которая до соударения покоилась.

 

Задача 13.69

На покоящийся шар налетает со скоростью v₁= 2 м/с другой шар одинаковой с ним массы. В результате столкновения этот шар изменил направление движения на угол α= 30^0. Определить: 1) скорости u₁ и u₂ шаров после удара; 2) угол β между вектором скорости второго шара и первоначальным направлением движения первого шара. Удар считать упругим.

 

Задача 13.70

Частица массой m₁=10-²⁴г имеет кинетическую энергию Т₁=9 нДж. В результате упругого столкновения с покоящейся частицей массой m₂ = 4*10 -²⁴ г она сообщает ей кинетическую энергию Т₂ =5 нДж. Определить угол α, на который отклонится частица от своего первоначального направления.

 

Задача 13.71

Пуля массой m = 12 г, летящая с горизонтальной скоростью v = 0,6 км/с, попадает в мешок с песком массой М = 10 кг, висящий на длинной нити, и застревает в нем. Определить: 1) высоту, на которую поднимется мешок, отклонившись после удара; 2) долю кинетической энергии, израсходованной на пробивание песка.

 

Задача 13.72

При центральном упругом ударе движущееся тело массой m₁ ударяется в покоящееся тело массой m₂, в результате чего скорость первого тела уменьшается в 2 раза. Определить: 1) во сколько раз масса первого тела больше массы второго тела; 2) кинетическую энергию Т’₂ второго тела непосредственно после удара, если первоначальная кинетическая энергия Т’₂ 1 первого тела равна 800 Дж.

 

Задача 13.73

Определить, во сколько раз уменьшится скорость шара, движущегося со скоростью v₁ при его соударении с покоящимся шаром, масса которого в n раз больше массы налетающего шара. Удар считать центральным и абсолютно упругим.

 

Задача 13.74

Тело массой m₁= 3 кг движется со скоростью v₁= 2 м/с и ударяется о неподвижное тело такой же массы. Считая удар центральным и неупругим, определить количество теплоты, выделившееся при ударе.

 

Задача 13.75

Тело массой m₁= 2 кг движется навстречу второму телу массой m₂=1,5 кг и неупруго сталкивается с ним. Скорость тел непосредственно перед столкновением была равна соответственно v₁= 1м/с и v₂ = 2 м/с. Сколько времени будут двигаться эти тела после столкновения, если коэфициент трения μ= 0,05?

 

Задача 13.76

Тело массой 5 кг ударяется о неподвижное тело массой 2,5 кг, которое после удара начинает двигаться с кинетической энергией 5 Дж. Считая удар центральным и упругим, найти кинетическую энергию первого тела до и после удара.

 

Задача 13.77

Два тела движутся навстречу друг другу и ударяются неупруго. Скорость первого тела до удара v₁= 2 м/c, скорость второго тела v₂ = 4 м/с. Общая скорость тел после удара по направлению совпадает с направлением скорости v₁ и равна v = 1 м/с. Во сколько раз кинетическая энергия первого тела была больше кинетической энергии второго тела?

 

Задача 13.78

Пуля, летящая горизонтально, попадает в шар, подвешенный на легком жестком стержне, и застревает в нем. Масса пули m₁= 5г и масса шара m₂=0,5кг. Скорость пули v₁ = 500 м/с. При какой предельной длине стержня ( расстояние от точки подвеса до центра шара) шар от удара пули поднимется до верхней точки окружности?

 

Задача 13.79

Движущееся тело массой пм ударяется о неподвижное тело массой пи. Считая удар упругим и центральным, найти, какую часть своей первоначальной энергии первое тело передает второму при ударе. Задачу решить сначала в общем виде, а затем рассмотреть случаи: 1) m₁=m₂ 2) m₁= 9m_2.

 

Задача 13.80

Два шара подвешены на параллельных нитях одинаковой длины так, что они соприкасаются. Масса первого шара 0,2 кг, масса второго шара 100 г. Первый шар отклоняют так, что его центр поднимается на высоту 4,5 см, и опускают. На какую высоту поднимутся шары после соударения, если: 1) удар упругий; 2) удар неупругий.

С уважением ИЦ "KURSOVIKS"!