42 Задачи с курса Физика на тему 11, Механическая энергия. Применение законов изменения и сохранения механической энергии (118 задач) 09.11.2018 21:37

Задача 11.1

Тормозной путь автомобиля, двигавшегося со скоростью v₁ = 30 км/ч, равен S₁ = 7,2 м. Чему будет равен тормозной путь, если скорость автомобиля увеличится до v₂ = 50 км/ч?

 

Задача 11.2

На тело массой m = 10 кг действует постоянная сила F = 5,0 Н. Определить кинетическую энергию тела через t = 2,0 с после начала движения. Сопротивлением пренебречь.

 

Задача 11.3

Какую работу надо совершить, чтобы заставить автомобиль массой М = 1,5 т: 1) увеличить свою скорость от 0 до 36 км/ч; 2) от 36 до 72 км/ч? Сопротивлением пренебречь.

 

Задача 11.4

Металлический шарик массой m = 100 г равномерно движется в горизонтальной плоскости по окружности радиусом R = 50 см с частотой n₁ =3 с^-1. Какую работу надо совершить, чтобы увеличить частоту до n₂ = 5 c^-1.

 

Задача 11.5

Определить кинетическую энергию тела массой 1 кг, брошенного горизонтально со скоростью v₀ = 20 м/с, в конце четвертой секунды его движения.

 

Задача 11.6

Тело, брошенное вертикально вверх, упало обратно через 4,0 с после начала движения. Определить кинетическую энергию в момент падения и потенциальную энергию в верхней точке, если масса тела 200 г.

 

Задача 11.7

По канатной железной дороге, идущей с углом наклона α = 45⁰ к горизонту, поднимается вагонетка массой m = 500 кг. Найти работу, которую совершает мотор подъемника, при поднятии вагонетки на высоту h = 10 м. Коэффициент трения принять равным µ = 10.

 

Задача 11.8

Тележка движется по горизонтальной дороге со скоростью 18 км/ч и въезжает на подъем. На какой высоте над уровнем дороги остановится тележка? Сопротивлением пренебречь.

 

Задача 11.9

На нити длиной l подвешен шар. Какую горизонтальную скорость нужно сообщить шару, чтобы он отклонился до высоты точки подвеса?

 

Задача 11.10

Пружина жесткостью k = 100 кН/м массой m = 400 г падает на Землю с высоты h = 5,0 м. На сколько сожмется пружина, если при ударе ее ось остается вертикально?

 

Задача 11.11

Тело брошено под углом к горизонту со скоростью v₀. Пользуясь законом сохранения механической энергии, определить скорость тела на высоте h над горизонтом.

 

Задача 11.12

Тело брошено вертикально вверх со скоростью v₀ = 20 м/с. На какой высоте h от точки бросания кинетическая энергия тела равна его потенциальной энергии?

 

Задача 11.13

Тело массой m = 100 г, брошенное вертикально вниз с высоты h = 20 м со скоростью v₁ = 10 м/с, упало на Землю со скоростью v₂ = 20 м/с. Найти работу по преодолению сопротивления воздуха.

 

Задача 11.14

Горный ручей с сечением потока S образует водопад высотой h. Скорость течения воды в ручье v. Найти мощность водопада.

 

Задача 11.15

Найти мощность воздушного потока, имеющего поперечное сечение в виде круга диаметром d = 18 м и движущегося со скоростью v = 12 м/с (воздух находится при нормальных условиях).

 

Задача 11.16

С ледяной горы высотой h = 1,0 м и основанием b = 5,0 м съезжают санки, которые останавливаются, пройдя горизонтальный путь l = 95 м. Найти коэффициент трения.

 

Задача 11.17

Какую горизонтальную скорость надо сообщить шарику, чтобы он сделал полный оборот в вертикальной плоскости, если он висит: 1) на легкой нити длиной l; 2) на жестком невесомом стержне длиной l?

 

Задача 11.18

Рис. 11.1 - Недеформированная легкая пружина, подвешенная к потолку

Недеформированную легкую пружину длины l₀, подвешенную к потолку в точке О, отклонили от вертикали на угол 90⁰, подсоединили к ней грузик массой m, который тут же отпустили. Определить скорость груза в момент прохождения вертикали ОА, если удлинение пружины составило l₀/2, а жесткость пружины равна k.

 

Задача 11.19

Какой путь пройдут сани по горизонтальной поверхности после спуска с горы высотой Н = 15 м, имеющей угол наклона α = 30⁰. Коэффициент трения саней о поверхность µ = 0,2.

 

Задача 11.20

Какая сила необходима для вытаскивания из доски гвоздя длиной l = 80 мм, если он забит шестью ударами молотка массой m = 0,5 кг при скорости молотка непосредственно перед ударом v = 2 м/с? Массой гвоздя пренебречь.

 

Задача 11.21

Веревка длиной l = 20 м переброшена через блок. В начальный момент веревка висит симметрично и покоится, а затем в результате незначительного толчка начинает двигаться по блоку, Будет ли движение веревки равноускоренным? Какова будет скорость веревки, когда она сойдет с блока? Массой блока пренебречь, радиус блока считать малым.

 

Задача 11.22

Рис. 11.2 - Вокруг горизонтальной оси О может свободно вращаться легкий рычаг

Вокруг горизонтальной оси О может свободно вращаться легкий рычаг, плечи которого равны l₁ и l₂ (см. рисунок). На концах рычага укреплены грузы с массами m₁ и m₂. Какую скорость v₁ будет иметь в нижней точке один из грузов, если первоначально рычаг находится в горизонтальном положении?

 

Задача 11.23

Цирковой гимнаст падает с высоты Н = 1,5 м на туго натянутую упругую предохранительную сетку. Каково будет максимальное провисание гимнаста в сетке, если в случае спокойно лежащего в сетке гимнаста провисание l₀ = 0,1 м?

 

Задача 11.24

Рис. 11.3 - Конечный участок горы разгона на лыжном трамплине

Конечный участок горы разгона на лыжном трамплине представляет собой дугу окружности радиуса R = 20 м (см. рисунок). Полная высота горы Н = 50 м. Найти ускорение прыгуна в точке В. Считать, что лыжник спускается из точки А без начальной скорости. Трением пренебречь.

 

Задача11.25

Тело массой m движется под действием постоянной силы F, Найти зависимость кинетической энергии тела от времени, если принять, что в начальный момент времени скорость равна нулю.

 

Задача 11.26

Два одинаковых шара подвешены на нитях l = 0,98 м и касаются друг друга. Один из шаров отклоняется на угол α = 10⁰ и отпускается. Определить максимальную скорость второго шара после соударения. Удар считать абсолютно упругим.

 

Задача 11.27

Найти силу F, действующую на тело, если потенциальная энергия тела имеет вид:

 

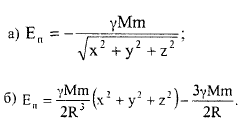
Задача 11.28

Модуль изменения импульса |∆p| камня, брошенного под углом к горизонту, за время полета равен 2,40 кгм/с. Дальность полета l = 5,00 м. Mасса камня m = 0,200 кг. Найти работу, совершенную при бросании камня.

 

Задача 11.29

Рис. 11.4 – Груз совершает колебания в некоторой плоскости

Груз массы m, подвешенный в точке О на длинной тонкой нити длины l, массой которой можно пренебречь, совершает колебания в некоторой плоскости. Наибольший угол отклонения нити от среднего положения равен α₀ (см. рисунок). Найти зависимость потенциальной Еn и кинетическую Ек энергии груза от угла α, приняв Еn равной нулю для груза в нижнем положении.

 

Задача 11.30

Шарик массой m = 0,100 кг, укрепленный на конце легкого стержня длины l = 1,27 м, вращается в вертикальной плоскости. В верхней точке шарик имеет скорость v₀ = 4,13 м/с. Найти потенциальную Е_n и кинетическую Е_k энергии шарика как функции угла α между стержнем и вертикалью. Положить α = 0 в нижней точке. Отсчет потенциальной энергии вести от нижнего положения.

 

Задача 11.31

Сила взаимодействия двух точечных электрических заряд определяется формулой F = k * (q₁q₂/r²), где q₁ и q₂ - заряды, k — коэффициент пропорциональности, зависящий от выбора системы единиц. Найти изменение потенциальной энергии взаимодействия двух положительных точечных зарядов q₁ и q₂ при изменении расстояния между ними от r₁ до r₂.

 

Задача 11.32

Рис. 11.5 - Угол склона α, радиус его закругления R, стартовая площадка лыжников

На каком минимальном расстоянии от места закругления склона должна располагаться стартовая площадка лыжников, чтобы они, достигнув закругления, начали свободный полет? Угол склона α, радиус его закругления R, коэффициент трения между лыжами и снегом µ < tgα. Стартовой скоростью лыжников пренебречь.

 

Задача 11.33

Потенциальная энергия частицы в некотором поле зависит от ее координаты r по закону Е_n (r) = a/r² – b/r, где а и b положительные постоянные. Найти: 1) функцию, определяющую зависимость проекции консервативной силы на ось r от координаты: F_r (r); 2) координату положения равновесия частицы в этом поле, характер равновесия (устойчивое, неустойчивое); 3) область координат, доступных для движения частицы, обладающей полной энергией Е_m = - b²/8a. Определить характер движения частицы в этой области. Какой должна быть минимальная энергия частицы, чтобы она могла достигнуть координаты r = 5a/b?

 

Задача 11.34

Рис. 11.6 - График зависимости энергии от координаты х

Частица массой m находится в одномерном поле консервативных сил. График зависимости энергии от координаты х представлен на рисунке. 1) Нарисовать примерный график зависимости проекции консервативной силы F_х(x). 2) Найти положение равновесия частицы. 3) Будет ли это равновесие устойчивым? 4) Определить область координаты х, доступную для движения частице, имеющей полную энергию Е_м = -1 * 10^-14 Дж; 5) Какой должна быть скорость частицы при х = 0, чтобы она могла достигнуть точки с координатой 10 мм? Описать характер движения.

 

Задача 11.35

Рис. 11.7 - Маленький брусок скользит без трения с высоты Н = 2R по наклонному желобу

Маленький брусок скользит без трения с высоты Н = 2R по наклонному желобу, переходящему в «мертвую петлю» радиусом R (см. рисунок). На какой высоте h брyсок оторвется от поверхности желоба? Какое давление брусок оказывает на желоб в тот момент, когда его скорость направлена вертикально вверх? С какой минимальной высоты Н_min должен соскальзывать брусок, чтобы он мог пройти петлю целиком?

 

Задача 11.36

Камень массой m = 2 кг брошен вертикально вниз с высоты Н = 250 м с некоторой начальной скоростью v₀. Камень погрузился в грунт на глубину h = 0,2 м. Считая, что средняя сила сопротивления грунта F = 2,7*10⁴ Н, определить начальную скорость камня v₀. Сопротивлением воздуха пренебречь.

 

Задача 11.37

Рис. 11.8 - Сила, действующая на снаряд массой m в стволе орудия, нарастает

Сила, действующая на снаряд массой m в стволе орудия, нарастает равномерно от нуля до F₀ на участке ствола длиной l₁ и равномерно уменьшается на участке ствола l₃ (см, рисунок). Какова скорость снаряда при вылете из ствола?

 

Задача 11.38

Спутник летит на высоте 300 км. Какую минимальную добавочную скорость ему нужно сообщить, чтобы он стал искусственным спутником Солнца? Орбиту считать круговой.

 

Задача 11.39

Найти вторую космическою скорость для Луны v_2Л (т.е. скорость, которой должна обладать ракета, стартующая с поверхности Луны, чтобы выйти из сферы лунного притяжения).

 

Задача 11.40

Спутник массой m = 5*10² кг выведен на круговую орбиту на высоту Н = 10³ км от поверхности Земли. Рассчитать изменение потенциальной энергии спутника в поле силы тяжести Земли. Радиус Земли R_з = 6,4*10³ км.

 

Задача 11.41

Космический корабль движется к Луне под влиянием ее притяжения. На большом расстоянии скорость корабля относительно Луны была нулевой. Ускорение силы тяжести на поверхности Луны в n = 6 раз меньше, чем на поверхности Земли. Радиус Луны R_JI = 1700 км. На какой высоте Н должен быть включен тормозной двигатель для осуществления мягкой посадки, если считать, что двигатель создает пятикратную перегрузку. Изменением массы корабля за счет сгорания топлива пренебречь. Считать Н << R_Л.

 

Задача 11.42

Груз свободно падает с высоты Н и погружается в глину на глубину h_1. Определить, какой слой песка следует насыпать на глину, чтобы груз углубился в глину на глубину h₂, если средняя сила сопротивления глины в два раза больше средней силы сопротивления песка.

 

Задача 11.43

Шар массой m = 2,6 кг падает без начальной скорости с высоты h = 55 см на расположенную вертикально пружину, которая при ударе сжимается. Найти величину наибольшего сжатия пружины, если ее коэффициент жесткости равен k = 72 H/м.

 

Задача 11.44

Груз массой m медленно втаскивают по наклонной плоскости на высоту h, затратив на это работу А. На этой высоте груз срывается и скользит обратно. Какую скорость он будет иметь у основания?

 

Задача 11.45

Вагон массой m = 20 т, двигаясь со скоростью v = 0,5 м/с, ударяется в два неподвижных буфера. Найти наибольшее сжатие буферов, если один буфер сжимается на ∆х₀ = 1см при действии силы F₀ = 50 кН.

 

Задача 11.46

Рис. 11.9 - Два одинаковых тела массой m каждое соединены пружиной жесткостью k и лежат на горизонтальной плоскости

Два одинаковых тела массой m каждое соединены пружиной жесткостью k и лежат на горизонтальной плоскости (см. рисунок). Какую минимальную скорость v, направленную к стене, надо сообщить правому телу, чтобы при обратном движении от стены оно сдвинуло левое тело? Коэффициент трения о плоскость µ. Пружина в начальный момент недеформирована.

 

Задача 11.47

Горный ручей с сечением потока S образует водопад высотой h. Скорость течения воды в ручье v. Найти мощность водопада.

 

Задача 11.48

Какой мощности двигатель должен иметь автомобиль массой m = 1,5 т, чтобы, трогаясь с места, за τ = 10 с при постоянной силе тяги мотора набрать скорость v = 100 км/ч? Сопротивлением воздуха пренебречь.

 

Задача 11.49

На катер действует сила сопротивления, пропорциональная квадрату скорости катера. Во сколько раз нужно увеличить мощность двигателя, чтобы скорость катера возросла в два раза?

 

Задача 11.50

Самолет для взлета должен иметь скорость v = 25 м/с. Длина пробега перед взлетом S = 100 м. Какова мощность моторов самолета, если его масса m = 1000 кг, а коэффициент сопротивления k = 0,02? Считать движение самолета при взлете равноускоренным, а силу сопротивления пропорциональной весу самолета.

 

Задача 11.51

Пуля, летящая с некоторой скоростью, углубляется в стенку на расстояние h = 10 см. На какое расстояние углубляется в ту же стенкy пуля, которая бyдет иметь скорость вдвое большую?

 

Задача 11.52

Пуля пробивает доску толщиной h = 3,6 см и продолжает полет со скоростью, равной α = 0,8 начальной скорости. Какой  максимальной толщины доску из того же материала она может пробить?

 

Задача 11.53

Пуля, летящая со скоростью v, пробивает несколько одинаковых досок, расположенных друг за другом на небольшом расстоянии. В какой по счету доске застрянет пуля, если ее скорость после прохождения первой доски равна v₁ = 0,83v?

 

Задача 11.54

Тело скользит вниз по наклонной плоскости. Угол наклона плоскости к горизонту α = 20⁰, длина ее l = 4 м, коэффициент трения тела о плоскость µ = 0,2. С какой скоростью будет двигаться тело в момент перехода с наклонной плоскости на горизонтальную поверхность?

 

Задача 11.55

Санки с ребенком общей массой т спускаются с горки произвольного профиля с высотой Н и останавливаются на горизонтальном участке. Какую работу нужно совершить, чтобы втащить санки с ребенком по тому же пути в гору? Ускорение свободного падения g.

 

Задача 11.56

Небольшое тело соскальзывает без начальной скорости с вершины гладкой горки высотой Н, имеющей горизонтальный трамплин (участок отрыва). При какой высоте h площадки отрыва тело пролетит наибольшее расстояние? Чему оно равно?

 

Задача 11.57

Рис. 11.10 - В брусок ударяет скатывающийся сверхy шарик

В брусок массой m₁, находящийся в равновесии на наклонной плоскости с углом при основании α и коэффициентом трения µ > tgα, ударяет скатывающийся сверхy шарик массой m₂, выполненный из того же материала, что и брусок (см. рисунок). После абсолютно неупругого удара брусок некоторое время приходит в движение, а затем останавливается. Определить путь S, пройденный им, если в момент удара шарик имел скорость v, а на деформацию затрачена доля первоначальной полной механической энергии системы, равна η.

 

Задача 11.58

Рис. 11.11 - Тело со скоростью начинает двигаться вверх по наклонной плоскости

Тело со скоростью v = 10 м/с начинает двигаться вверх по наклонной плоскости с углом при основании α = 30⁰ коэффициентом трения µ = 0,3. На высоте h = 1 м тело упруго ударяется о преграду (см. рисунок). Определить скорость v₀ тела у основания наклонной плоскости после удара.

 

Задача 11.59

Автомобиль с работающим двигателем въезжает на обледенелую гору, поверхность которой образует угол α с горизонтом. Какой высоты h гору может преодолеть автомобиль, если его начальная скорость при въезде равна v₀, а коэффициент трения колес о лед µ < tgα?

 

Задача 11.60

Рис. 11.12 - С вершины сферы соскальзывает без трения небольшое тело

Сфера радиусом R укреплена на горизонтальном полу. С вершины сферы соскальзывает без трения небольшое тело (см. рисунок). На каком расстоянии l от точки закрепления сферы упадет это тело на пол? Трением пренебречь.

 

Задача 11.61

Рис. 11.13 - Шарик без трения может катиться по желобу

Шарик без трения может катиться по желобу, изображенному на рисунке. С какой минимальной высоты нужно пустить шарик, чтобы он не покинул желоб по всей его длине? Радиус закругления желоба R известен. Трения нет.

 

Задача 11.62

Рис. 11.14 - Небольшое тело А начинает скользить с высоты h по наклонному желобу

Небольшое тело А начинает скользить с высоты h по наклонному желобу, переходящему в полуокружность радиусом h/2 (см. рисунок). Пренебрегая трением, найти скорость тела в наивысшей точке его траектории (после отрыва от желоба).

 

Задача 11.63

Шар подвешен на невесомой нерастяжимой нити. Его отклонили от положения равновесия до высоты точки подвеса и отпустили. При каком значении угла α между нитью и вертикалью нить оборвется, если известно, что нить выдерживает силу натяжения, равную 2 mg?

 

Задача 11.64

На невесомом резиновом шнуре закреплено тело массой m = 0,5 кг. Тело отклоняют до горизонтального положения, не растягивая шнур. На сколько растянется шнур, когда отпущенное тело проходит нижнюю точку траектории? Упругость шнура равна k = 50 Н/м.

 

Задача 11.65

На тонкой нерастяжимой нити подвешен шарик. Нить приводят в горизонтальное положение и отпускают. В каких точках траектории полное ускорение шарика направлено горизонтально?

 

Задача 11.66

Шарик висит на невесомой нерастяжимой нити длиной l. Определить минимальную величину скорости, которую надо сообщить шарику в горизонтальном направлении, чтобы он совершил один полный оборот вокруг точки подвеса. Трением и сопротивлением воздуха пренебречь.

 

Задача 11.67

Рис. 11.15 – Пуля попадает в шар, подвешенный на невесомой нерастяжимой нити

Пуля массой m = 5 г, летевшая горизонтально со скоростью v = 500 м/с, попадает в шар массой М = 0,5 кг, подвешенный на невесомой нерастяжимой нити, и застревает в нем (см. рисунок). При какой наибольшей длине нити шар совершит полный оборот по окружности?

 

Задача 11.68

Рис. 11.16 - Два одинаковых шарика, соединенные невесомой нерастяжимой нитью длиной l, падают с высоты h

Два одинаковых шарика массой m каждый, соединенные невесомой нерастяжимой нитью длиной l, падают с высоты h так, что нить своей нижней точкой налетает на горизонтально расположенный гвоздь (см. рисунок). Какой должна быть минимальная высота h, чтобы нить оборвалась? Предельное натяжение нити Т₀. Сопротивлением воздуха пренебречь.

 

Задача 11.69

Рис. 11.17 - На расстоянии а от точки подвеса вбит гвоздь

На нити длиной l подвешен маленький шарик. Нить отводят до горизонтального положения и отпускают. На расстоянии а от точки подвеса вбит гвоздь (см. рисунок). На какую максимальную относительно гвоздя высоту поднимется шарик при движении? Точка подвеса и гвоздь находятся на одной вертикали.

 

Задача 11.70

Тонкий обруч радиусом R раскрутили вокруг его оси до угловой скорости w и положили плашмя на горизонтальный стол. Коэффициент трения между поверхностью стола и обручем равен µ. Сколько оборотов сделаeт обруч до остановки?

 

Задача 11.71

Под действием постоянной силы F = 400Н, направленной вертикально вверх, груз массой m = 20 кг был поднят на высоту h = 15 м. Какой потенциальной энергией П будет обладать поднятый груз? Какую работу А совершит сила F?

 

Задача 11.72

Тело массой m = 1 кг, брошенное с вышки в горизонтальном направлении со скоростью v₀ = 20 м/с, через t = 3 с упало на Землю. Определить кинетическую энергию Т, которую имело тело в момент удара о Землю. Сопротивлением воздуха пренебречь.

 

Задача 11.73

Камень брошен вверх под углом φ = 60⁰ к плоскости горизонта. Кинетическая энергия Т₀ камня в начальный момент времени равна 20 Дж. Определить кинетическую Т и потенциальную П энергии камня в высшей точке его траектории. Сопротивлением воздуха пренебречь.

 

Задача 11.74

Какова мощность N воздушного потока сечениием S = 0,55 м² при скорости воздуха v = 20 м/с и нормальных условиях?

 

Задача 11.75

Камешек скользит с наивысшей точки купола, имеющего фор полусферы. Какую дугу α опишет камешек, прежде чем оторваться о поверхности купола? Трением пренебречь.

 

Задача 11.76

Мотоциклист едет по горизонтальной дороге. Какую наименьшую скорость v он должен развить, чтобы, выключив мотор, проехать по треку имеющему форму «мертвой петли» радиусом R = 4 м? Трением и сопротивлением воздуха пренебречь.

 

Задача 11.77

При выстреле из орудия снаряд массой rn₁ = 10 кг получает кинетическую энергию Т₁ = 18 МДж. Определить кинетическую энергию Т₂ ствола орудия вследствие отдачи, если масса m₂ ствола орудия равна 600 кг.

 

Задача 11.78

Ядро атома распадается на два осколка массами m₁ = 1,6*10^-25 кг и m₂ = 24*10²⁵ кг. Определить кинетическую энергию Т₂ второго осколка, если энергия Т₁ первого осколка равна 18 нДж.

 

Задача 11.79

Конькобежец, стоя на льду, бросил вперед гирю массой m₁ = 5 кг и вследствие отдачи покатился назад со скоростью v₂ = 1 м/с. Масса конькобежца m₂ = 60 кг. Определить работу А, совершенную конькобежцем при бросании гири.

 

Задача 11.80

Молекула распадается на два атома. Масса одного из атомов в n = 3 раза больше, чем другого. Пренебрегая начальной кинетической энергией и импульсом молекулы, определить кинетические энергии Т₁ и Т₂ атомов, если их суммарная кинетическая энергия Т = 0,032 нДж.

 

Задача 11.81

Тело массой m = 5 кг падает с высоты h = 20 м. Определить сумму потенциальной и кинетической энергий тела в точке, находящейся от поверхности Земли на высоте h₁ = 5 м. Трением тела о воздух пренебречь. Сравнить эту энергию с первоначальной энергией тела.

 

Задача 11.82

Тело, падая с некоторой высоты, в момент соприкосновения с Землей обладает импульсом р = 100 кг*м/с и кинетической энергией Т = 500 Дж. Определить: 1) с какой высоты тело падало; 2) массу тела.

 

Задача 11.83

Автомашина массой m = 2000 кг останавливается за t = 6 с, пройдя расстояние S = 30 м. Определить: 1) начальную скорость автомашины; 2) силу торможения.

 

Задача 11.84

Материальная точка массой m = 20 г движется по окружности радиусом R = 10 см с постоянным тангенциальным ускорением. К концу 5-го оборота после начала движения кинетическая энергия материальной точки оказалась равной 6,3 мДж. Определить тангенциальное ускорение.

 

Задача 11.85

Ядро массой m = 5 кг бросают под углом α = 60⁰ к горизонту, затрачивая при этом работу 500 Дж. Пренебрегая сопротивлением воздуха, определить: 1) через какое время ядро упадет на Землю; 2) какое расстояние по горизонтали оно пролетит.

 

Задача 11.86

Тело массой m = 0,5 кг бросают со скоростью v₀ = 10 м/с под углом α = 30⁰ к горизонту. Пренебрегая сопротивлением воздуха определить кинетическую Т, потенциальную П и полную Е энергии тела: 1) через t = 0,4 с после начала движения; 2) в высшей точке траектории.

 

Задача 11.87

К нижнему концу пружины жесткостью k₁, присоединена дрyгая пружина жесткостью k₂, к концу которой прикреплена гиря. Пренебрегая массой пружин, определить отношение потенциальных энергий пружин.

 

Задача 11.88

Тело массой m = 0,4 кг скользит по наклонной плоскости высотой h = 10 см и длиной l = 1 м. Коэффициент трения на всем пути µ = 0,04. Определить: 1) кинетическую энергию тела у основания плоскости; 2) путь, пройденный телом на горизонтальном участке до остановки.

 

Задача 11.89

Тело брошено вертикально вверх со скоростью v₀ = 20 м/с. Пренебрегая сопротивлением воздуха, определить, на какой высоте h кинетическая энергия тела будет равна его потенциальной энергии.

 

Задача 11.90

Тело массой m = 70 кг движется под действием постоянной силы F = 63Н. Определить, на каком пути S скорость этого тела возрастет в n = 3 раза по сравнению с моментом времени, когда скорость тела была равна v₀ = 1,5 м/с.

 

Задача 11.91

Тело брошено под углом α = 45⁰ к горизонту со скоростью v₀ = 15 м/с, Используя закон сохранения энергии, определить скорость v тела в высшей точке его траектории.

 

Задача 11.92

Спортсмен с высоты h = 12 м падает на упругую сетку. Пренебрегая массой сетки, определить во сколько раз наибольшая сила давления спортсмена на сетку больше его силы тяжести, если прогиб сетки под действием силы тяжести спортсмена х₀ = 15 см.

 

Задача 11.93

Рис. 11.18 - Два цилиндра, соединенные сжатой пружиной, разошлись при внезапном освобождении пружины в разные стороны

Два цилиндра массами m₁ = 150 г и m₂ = 300 г, соединенные сжатой пружиной, разошлись при внезапном освобождении пружины в разные стороны. Пренебрегая силами сопротивления и учитывая, что кинетическая энергия упругой деформации пружины составляет 1,8 Дж, определить: 1) скорость v₁ движения первого цилиндра; 2) скорость v₂ движения второго цилиндра.

 

Задача 11.94

Рис. 11.19 – Гиря падает с высоты на подставку, скрепленную с пружиной

Гиря массой m = 10 кг падает с высоты h = 0,5 м на подставку, скрепленную с пружиной жесткостью k = 30 Н/см (см. рисунок). Определить при этом смещение х пружины.

 

Задача 11.95

Зависимость потенциальной энергии П тела в центральном силовом поле от расстояния r до центра поля задается функцией П(г) = A/r² - B/r (А = 6 мкДж*м², В = 0,3 мкДж*м). Определить, при каких значениях r максимальное значение принимают: 1) потенциальная энергия тела; 2) сила, действующая на тело.

 

Задача 11.96

Сила, действующая на тело в некотором поле консервативных сил, описывается законом F = A(yi + хј), где А — некоторая постоянная; i и ј — соответственно единичные векторы координатных осей х и у. Определить потенциальную энергию П(х,у) тела в этом положении.

 

Задача 11.97

Какую работу надо совершить, чтобы заставить движущееся тело массой 2 кг: 1) увеличить свою скорость от 2 до 5 м/с; 2) остановиться при начальной скорости 8 м/с.

 

Задача 11.98

Мяч, летящий со скоростью v₁ = 15 м/с, отбрасывается ударом ракетки в противоположном направлении со скоростью v₂ = 20 м/с. Найти, чему равно изменение количества движения мяча, если известно, что изменение его кинетической энергии при этом равно ∆Е_к = 8,75 Дж.

 

Задача 11.99

Вагон массой 20 т, движущийся равнозамедленно, под действием силы трения 6000 Н через некоторое время останавливается. Найти: 1) работу сил трения; 2) расстояние, которое вагон пройдет до остановки.

 

Задача 11.100

Шофер автомобиля начинает тормозить в 25 м от препятствия на дороге. Сила трения в тормозных колодках автомобиля 1 Т. При какой предельной скорости движения автомобиль успеет остановиться перед препятствием? Трением колес о дорогу пренебречь.

 

Задача 11.101

Трамвай движется с ускорением а = 49 см/с². Найти коэффициент трения, если известно, что 50%. Мощности мотора идет на преодоление сил трения и 50% - на увеличение скорости движения.

 

Задача 11.102

Найти работу, которую надо совершить, чтобы увеличить скорость движения тела от 2 до 6 м/с на пути 10 м. На всем пути действует постоянная сила трения 1,96 Н. Масса тела 1 кг.

 

Задача 11.103

Камень 2 кг упал с некоторой высоты. Падение продолжалось 1,43 с. Найти кинетическую и потенциальную энергии камня в средней точке пути. Сопротивлением пренебречь.

 

Задача 11.104

С башни высотой Н = 25 м горизонтально брошен камень со скоростью v₀ = 15 м/с. Найти кинетическую и потенциальную энергии камня спустя одну секунду после начала движения. Масса камня m = 0,2 кг. Сопротивлением воздуха пренебречь.

 

Задача 11.105

Камень бросили под углом α = 60⁰ к горизонту со скоростью v₀ = 15 м/с. Найти кинетическую, потенциальную и полную энергии камня: 1) спустя одну секунду после начала движения; 2) в высшей точке траектории. Масса камня m = 0,2 кг. Сопротивлением воздуха пренебречь.

 

Задача 11.106

Материальная точка массой 10 г движется по окружности радиусом 6,4 см с постоянным тангенциальным ускорением. Найти величину тангенциального ускорения, если известно, что к концу второго оборота после начала движения кинетическая энергия материальной точки стала равной 8*10^-4 Дж.

 

Задача 11.107

Тело скользит по наклонной плоскости, составляющей угол α = 8⁰ с горизонтом, а затем по горизонтальной поверхности. Найти, чему равен коэффициент трения, если известно, что тело проходит по горизонтали такое же расстояние, как и по наклонной плоскости.

 

Задача 11.108

Найти наибольшую величину прогиба рессоры от груза, положенного на ее середину, если статический прогиб рессоры от того же груза х₀ = 2 см. Сила тяжести груза равна Р. Каков будет наибольший начальный прогиб, если на середину рессоры падает тот же груз с высоты h = 1 м без начальной скорости?

 

Задача 11.109

Акробат прыгает в сетку с высоты Н₁ = 8 м. На какой предельной высоте h₁ над полом надо натянуть сетку, чтобы акробат не ударился о пол при прыжке? Известно, что сетка прогибается на h₂ = 0,5 м, если акробат прыгает в нее с высоты Н₂ = 1 м.

 

Задача 11.110

Груз массой m = 1 кг, висящий на невесомом стержне длиной l = 0,5 м, совершает колебания в вертикальной плоскости. 1) При каком угле отклонения α стержня от вертикали кинетическая энергия груза в его нижнем положении равна Е_к = 2,45 Дж? 2) Во сколько раз при таком угле отклонения натяжение стержня в его среднем положении больше натяжения стержня в его крайнем положении?

 

Задача 11.111

На чашку весов падает груз массой 1 кг с высоты 10 см. Каковы показания весов в момент удара? Известно, что под действием этого груза после успокоения качаний чашка весов опускается на 0,5 см.

 

Задача 11.112

Мальчик, стреляя из рогатки, натянул резиновый шнур так, что его длина стала больше на 10 см. С какой скоростью полетел камень массой 20 г? Для натягивания резинового шнура на 1 см требуется сила 9,8 Н. Сопротивлением воздуха при полете камня пренебречь.

 

Задача 11.113

Два медных шарика диаметрами d₁ = 4 см и d₂ = 6 см находятся в соприкосновении друг с другом. Найти гравитационную потенциальную энергию этой системы.

 

Задача 11.114

Во сколько раз кинетическая энергия искусственного спутника Земли, движущегося по круговой траектории, меньше его гравитационной потенциальной энергии?

 

Задача 11.115

Найти отношение затрат энергии на поднятие спутника на высоту h = 3200 км и на последующий запуск его по круговой орбите на той же высоте. Радиус Земли R₃ = 6400 км.

 

Задача 11.116

Спутник массой m = l000 кг вращается по круговой орбите вокрyг Земли на высоте h = 1000 км от ее поверхности. Каковы его потенциальная, кинетическая и полная энергии? Масса Земли M₃ = 5,96*10²⁴ кг, радиус Земли R₃ = 6400 км.

 

Задача 11.117

Космический корабль летит от Земли к Луне, все время перемещаясь вдоль прямой, соединяющей центры планеты и спутника. На каком расстоянии h от Земли потенциальная энергия корабля принимает наибольшее значение? Массы Земли и Луны М₁ и М₂ соответственно. Расстояние между центрами Земли и Луны равно R.

 

Задача 11.118

Спутник движется со скорость v по круговой орбите вокруг Земли. Какую наименьшую добавочную скорость надо сообщить спутнику, чтобы он мог покинуть поле притяжения Земли?

С уважением ИЦ "KURSOVIKS"!