38 Задачи с курса Физика на тему 7, Импульс материальной точки и системы материальных точек. Законы изменения и сохранения импульса (77 задач) 09.11.2018 20:34

Задача 7.1

Рис. 7.1 - Молекула массой m ударяется о стенку сосуда

Молекула массой m, летящая к стенке сосуда со скоростью v, ударяется о нее и упруго отскакивает без потери скорости. а) Найти импульс силы, полученный стенкой при ударе молекулы о стенку, в направлении нормали. б) Найти импульс силы, полученный стенкой при ударе молекулы, летящей к ней под углом α. Решить задачу в системе отсчета, связанной с наклонной плоскостью.

 

Задача 7.2

Футболист, ударяя мяч массой m = 700 г, сообщает ему скорость v = 15 м/с. Считая длительность удара равной t = 0,020 с, определить среднюю силу удара.

 

Задача 7.3

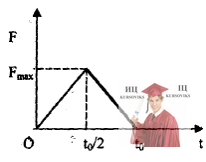
Рис. 7.2 – Скорость мяча

Какую скорость может сообщить футболист мячу при ударе, если максимальная сила, с которой он может действовать на мяч, F_max = 3,5 * 10³ H, время удара t₀ = 8 * 10³ с? Считать, что сила во время удара нарастает и спадает по линейному закону, как показано на графике. Масса мяча m = 0,5 кг.

 

Задача 7.4

Футболист бьет по мячу со средней силой F = 5 * 10² Н. Мяч после удара улетает под углом α = 45⁰ к горизонту и приземляется на расстоянии L = 40 м. Определить время удара по мячу. Сопротивлением воздуха пренебречь. Масса мяча m = 0,5 кг.

 

Задача 7.5

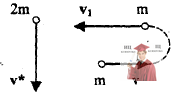
Рис. 7.3 – Две частицы

На две частицы – одну массы m, летящую со скоростью v, другую массы 2m, летящую со скоростью |v^*| = 2v, перпендикулярно к первой в течение некоторого времени действуют одинаковые по модулю и направлению силы. К моменту прекращения действия сил первая частица начинает двигаться в обратном направлении со скоростью |v₁| = 2v. С какой скоростью будет двигаться при этом вторая частица?

 

Задача 7.6

Два одинаковых шарика массами m = 2,0 г движутся в горизонтальной плоскости с одинаковыми скоростями v = 4,0 м/с: 1) вдоль одной пумой навстречу друг другу; 2) вдоль одной прямой один за другим; 3) под углом α = 120⁰ друг другу. Чему равен суммарный импульс этих шариков во всех случаях?

 

Задача 7.7

Тело равномерно движется по окружности со скоростью v. Найти изменение импульса движения тела при повороте на 60, 90, 180 и 360⁰.

 

Задача 7.8

Шарик массой m = 10 г падает на горизонтальную плоскость с высоты h₁ = 22,5 см. Найти среднюю силу удара в следующих случаях: 1) шарик пластилиновый; 2) шарик стальной, после удара отскакивает на высоту h₁; 3) шарик пластмассовый, после удара отскакивает на высоту h₂ = 11 см. Длительность удара во всех случаях считать одинаковой и равной t = 0,030 с.

 

Задача 7.9

Рис. 7.4 - Две частицы массами m и 2m движутся во взаимно перпендикулярных направлениях

Две частицы массами m и 2m движутся во взаимно перпендикулярных направлениях со скоростями 2v и v (см. рисунок). На частицы начинает действовать одинаковая сила. Определить модуль и направление скорости частицы 2m в момент времени, когда скорость частицы массой m стала такой, как показано пунктиром: 1) на рисунке а; 2) на рисунке б.

 

Задача 7.10

Колесо массой m = 3,0 кг катится без проскальзывания по горизонтальной плоскости со скоростью v = 5,0 м/с. Определить импульс колеса.

 

Задача 7.11

Пожарный направляет струю воды из брандспойта на огонь. Скорость воды v = 16 м/с. Площадь брандспойта S = 5,0 см². Найти силу, с которой пожарный удерживает брандспойт.

 

Задача 7.12

Два тела, двигаясь навстречу друг другу со скоростью v = 3,0 м/с каждое, после соударения стали двигаться вместе со скоростью u = 1,5 м/с. Определить отношение масс этих сил. Трением пренебречь.

 

Задача 7.13

Тележка с песком катится со скоростью v₁ = 1 м/с. Навстречу тележке летит шар массой m = 2,0 кг с горизонтальной скоростью v₂ = 7,0 м/с. С какой скоростью (и в каком направлении) будет продолжаться движение этой тележки с застрявшим в песке шаром. Масса тележки с песком М = 10 кг.

 

Задача 7.14

По абсолютно гладкой поверхности движется со скоростью v = 6 м/с ящик с песком массой М = 9,0 кг. В песок попадает гиря массой m = 1,0 кг, отпущенная без начальной скорости с 10 - метровой высоты. Определить скорость ящика после попадания в него гири.

 

Задача 7.15

Доска массой m₁, свободно скользит по поверхности льда со скоростью v₁. На доску с берега прыгает человек массы m₂. Скорость человека горизонтальна и перпендикулярна к скорости доски и равна v₂. Определить скорость v доски с человеком, силой трения доски о лед пренебречь.

 

Задача 7.16

Рис. 7.5 - На гладком столе покоятся точечные массы 3m и 2m

На гладком столе покоятся точечные массы 3m и 2m, скрепленные невесомой жесткой штангой. На массу 3m налетает и прилипает к ней кусочек пластмассы массы m, двигавшейся со скоростью v₀ перпендикулярно штанге (см. рисунок). С какой скоростью должен двигаться наблюдатель, для которого движение штанги после соударения является чистым вращением? В каком отношении точка, вокруг которой происходит это вращение, делит штангу?

 

Задача 7.17

Рис. 7.6 - В заднюю стенку башни танка ударяется горизонтально летящая пуля

В заднюю стенку башни танка, идущего со скоростью u = 72 км/ч, ударяется горизонтально летящая со скоростью v₀ = 750 м/с пуля и упруго отскакивает от нее. С какой скоростью полетит отскочившая пуля? Стенка наклонена к вертикали под углом φ (см. рисунок).

 

Задача 7.18

Рис. 7.7 - На железнодорожной платформе укреплено орудие

На железнодорожной платформе, движущейся равномерно со скоростью v, укреплено орудие, ствол которого направлен в сторону движения платформы и приподнят над горизонтом на угол α. Орудие произвело выстрел, после чего скорость платформы уменьшилась в 3 раза. Найти скорость снаряда при вылете из ствола, если его масса m, а масса платформы с орудием равна М.

 

Задача 7.19

Рис. 7.8 - Шар массой m₁ движется со скоростью v₁ и упруго сталкивается с шаром массой m₂

Шар массой m₁ движется со скоростью v₁ и упруго сталкивается с шаром массой m₂, который двигался со скоростью v₂         под углом α траектории первого шара (см. рисунок). На какой угол β₁ отклонится первый шар после соударения, если второй отклонился на угол β по отношению первоначальной траектории первого шара, а скорость его стала равной v'₂?

 

Задача 7.20

С какой скоростью v стал двигаться стрелок, стоящий на гладком льду, если он сделал два горизонтальных выстрела: 1) в одном и том же направлении; 2) второй выстрел в направлении, перпендикулярном первому. Масса стрелка с винтовкой составляет М = 70 кг, масса пули m = 10 г и ее начальная скорость v₀ = 700 м/с.

 

Задача 7.21

Тело массой М = 300 г падает свободно с высоты Н = 10 м. На высоте Н/2 в тело попадает и застревает в нем пуля массой m = 10 г, летевшая горизонтально со скоростью v₀ = 400 м/с. Найти скорость тела и угол, который образует вектор скорости с горизонталью в момент после соударения.

 

Задача 7.22

Снаряд в верхней точке своей траектории разрывается на два осколка равной массы. Один осколок после взрыва возвращается к орудию по прежней траектории. Где упадет второй осколок? Сопротивление воз не учитывать.

 

3адача 7.23

Снаряд разрывается в верхней точке траектории на высоте Н = 15,9 м на две одинаковые части. Через время t = 3,00 с после взрыв одна часть падает на Землю под тем местом, где произошел взрыв. С какой скоростью и под каким углом к горизонту начала двигаться вторая час снаряда после взрыва, если первая упала на расстоянии l = 636 м от мест выстрела? Сопротивление воздуха не учитывать.

 

Задача 7.24

По наклонной плоскости, составляющей угол α горизонтом, начинает скользить без трения ящик с песком массой М. В тот момент, когда ящик прошел путь l, в него попало тело массой m, двигавшееся горизонтально. Ящик при этом остановился. С какой скоростью двигалось тело?

 

Задача 7.25

По наклонной плоскости с углом α = 30⁰ при основании равномернo скользит ящик с песком массой М = 10 кг со скоростью v = 1,0 м/с. Когда в ящик попадает пуля массой m = 10 г, летевшая горизонтально, ящик останавливается. Определить скорость пули.

 

Задача 7.26

С вершины клина с углом α = 45⁰ при основании с высоты Н = 20 см начинает скользить тело массой m = 0,50 кг. Клин лежит на абсолютно гладкой поверхности. Определить, на какое расстояние переместится клин, когда тело окажется у его основания. Масса клина М = 1,5 кг.

 

Задача 7.27

Человек захотел спуститься по веревочной лестнице из свободно висящего аэростата массой М = 350 кг. Какой минимальной длины веревочную лестницу он должен привязать к гондоле аэростата, чтобы, ступая на последнюю ступеньку, он коснулся Земли? Масса человека m = 70 кг. Расстояние от Земли до аэростата Н = 10 м.

 

Задача 7.28

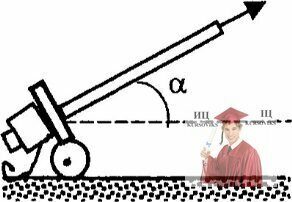
Рис. 7.9 – Выстрел из орудия, стоящего на горизонтальной площадке

Из орудия, стоящего на горизонтальной площадке, производится выстрел под углом α = 45⁰ к горизонту. Масса орудия m₀ = 5 т, масса снаряда m_с = 100 кг. В результате выстрела орудие откатилось за t = 5 с на расстояние S =10 м и остановилось. Определить скорость снаряда. Движение орудия — равнозамедленное.

 

Задача 7.29

Снаряд разрывается в верхней точке траектории на три равные части. Начальные скорости осколков лежат в горизонтальной плоскости. Скорость первого осколка направлена вдоль, а скорости второго и третьего осколков — перпендикулярно к скорости снаряда. Точка поверхности Земли, над которой происходит разрыв снаряда, находится на расстоянии l от места выстрела. В системе отсчета, связанной с центром инерции снаряда, скорости осколков одинаковы. Определить l₁, l₂ и l₃ от точки ”О” до места падения первого, второго и третьего осколков.

 

Задача 7.30

По гладкой наклонной плоскости скользит ящик с песком массы М. После того, как ящик прошел путь S, в него попадает камень массы m, летящий под углом β к горизонту. Какова была скорость камня v, если ящик с песком после попадания в него камня остановился? Угол наклона плоскости к горизонту α (α < β). Скорости камня и ящика лежат в одной плоскости.

 

Задача 7.31

Тело массой m движется вдоль перпендикулярного к стенке направления со скоростью v₁. Стенка движется вдоль того же направления со скоростью v₂. Найти изменение импульса тела ∆р при упругом ударе его со стенкой. Определить изменение проекции импульса тела ∆p_v на направление скорости в случае v₁, если стенка движется навстречу телу.

 

Задача 7.32

Струя воды ударяется о гранитную стенку под углом α = π/3 к нормали и упруго отражается от нее с такой же по модулю скоростью. Найти давление струи на стенку, если скорость воды в струе v = 12 м/с. Плотность воды ρ = 10³ кг/м³. Как изменится решение задачи, если стенка пористая и скорость струи при соприкосновении со стенкой целиком гасится?

 

Задача 7.33

На конце длинной тележки массой m₁ = 20 кг стоит человек массой m₂ = 60 кг, который начинает идти вдоль тележки с относительной скоростью v' = l м/с. Пренебрегая массами колес и силой трения, определить скорость тележки.

 

Задача 7.34

Шар массой m = 0,15 кг скользит по гладкой горизонтальной плоскости со скоростью v = 6 м/с и ударяется о гладкую вертикальную стенку так, что угол между векторами скоростей до и после удара равен α = π/3. Считая удар упругим, определить продолжительность удара, если известно, что средняя сила удара F = 200 Н.

 

Задача 7.35

Два мальчика массой m₁, каждый стоят на конце плота массой m₂. Мальчики последовательно прыгают с плота в воду в одном направлении, причем горизонтальная скорость мальчиков относительно плота одинакова и равна v₀. Какую скорость приобретает плот после прыжка первого мальчика и после прыжка второго мальчика? Будет ли скорость, которую приобретает плот после прыжка второго мальчика, больше или меньше той скорости, которую приобрел бы плот, если бы оба мальчика прыгнули одновременно? Сопротивлением воды пренебречь.

 

Задача 7.36

Молот массой m = 10 кг падает на горячую поковку с высоты h = 1,25 м. Найти среднюю силу, действующую на поковку, если удар абсолютно неупругий, а время удара t = 0,01 с.

 

Задача 7.37

Найти скорость, которую приобретает тело массой m = 1 кг через t = 10 с после начала движения под действием единственной переменной силы, зависимость модуля которой от времени имеет вид: F = -c₁t² + c₂t, где c₁ = 0,2 Н/с², c₂ = 2 Н/с.

 

Задача 7.38

Грузовой автомобиль массой m₁ = 3 * 10³ кг движется по инерции со скоростью v₁ = 20 м/с. Когда он проезжал под эстакадой, в кузов упал сверху предмет массой m₂ = 100 кг. Предмет продолжал некоторое время двигаться вместе с автомобилем, затем он выпал из кузова. Пренебрегая сопротивлением движению, определить, как будет меняться скорость автомобиля.

 

Задача 7.39

На краю неподвижной платформы, имеющей длину l и массу m₁, сидит лягушка массой m₂. С какой минимальной скоростью должна она прыгнуть, чтобы попасть на другой конец платформы? Платформа находится на гладкой поверхности.

 

Задача 7.40

На массивную плиту вертикально вниз падает мяч массой m, скорость которого в момент касания равна v. После упругого взаимодействия мяч отскакивает вверх. Оценить среднюю силу, действующую на плиту при ударе, если время взаимодействия равно ∆t.

 

Задача 7.41

Игрок в пинг-понг ударяет в горизонтальном направлении шарик массой m так, чтобы тот перелетел стол длиной l. С какой минимальной средней силой должен действовать игрок на шарик во время удара? Считать, что шарик ударяется на высоте h над столом, время удара ∆t, скорость шарика до удара равна нулю. Сопротивлением воздуха пренебречь.

 

Задача 7.42

Кубик из пенопласта массой М = 10 г лежит на горизонтальной подставке. Скорость пули за время движения в кубике изменяется от v₁ = 100 м/с до v₂ = 95 м/с. Определить скорость кубика после вылета пули. Масса пули 9 г.

 

Задача 7.43

Небольшой шарик налетает на неподвижную стенку под углом α к нормали. Коэффициент трения о стенку µ. Под каким углом шарик отлетит от стенки?

 

Задача 7.44

Струя воды, вытекающая из трубы диаметром d = 2 см со скоростью v = 0,5 м/с, ударяется о вертикальную стенку. Определить действующую на стенку силу, считая, что труба расположена к стенке под прямым углом, а удар абсолютно неупругий. Плотность воды р =10 ³ кг/м³.

 

Задача 7.45

Лодка длиной l и массой М стоит на спокойной воде носом к берегу. Как изменится расстояние между носом лодки и берегом, если человек массой m перейдет с кормы на нос лодки? Сопротивлением воды пренебречь.

 

Задача 7.46

Однородный стержень длиной l одним концом касается гладкой горизонтальной поверхности. Верхний конец стержня подвешен на нити так, что стержень образует с горизонтальной плоскостью угол α. Нить пережигают. В какую сторону и на сколько сместится нижний конец стержня, когда он упадет?

 

Задача 7.47

Тело массой m брошено горизонтально. Определить величину изменения импульса тела за время, в течение которого оно по вертикали опустится на расстояние h. Сопротивлением воздуха пренебречь.

 

Задача 7.48

В результате упругого столкновения с неподвижной преградой тело отклонилось от своего первоначального направления движения на угол α, Определить величину изменения импульса тела, если его масса m, а скорость в момент удара v.

 

Задача 7.49

Небольшое тело массой m двигалось прямолинейно с постоянной скоростью v. В результате упругого столкновения с движущейся преградой тело отклоняется от своего первоначального направления движения. При этом импульс тела изменяется на величину ∆р. Определить угол, на который отклоняется тело, и скорость тела после столкновения, если известно, что вектор ∆р перпендикулярен вектору v.

 

Задача 7.50

Снаряд, летящий со скоростью v = 300 м/с, разрывается в воздухе на два осколка. Один, массой m₁ = 3 кг, сохраняет первоначальное направление движения снаряда и имеет скорость v₁ = 600 м/с. Какова скорость v₂ и направление движения второго осколка, если его масса равна m₂ = 2 кг?

 

Задача 7.51

Снаряд в верхней точке параболической траектории разрывается на два осколка равной массы. Один осколок возвращается к исходной точке вылета снаряда по его прежней траектории. Сравнить расстояние от исходной точки до места падения второго осколка с дальностью полета снаряда, если бы он не разорвался. Сопротивлением воздуха пренебречь.

 

Задача 7.52

Снаряд, летевший по вертикали, разрывается в верхней точке траектории на три равных осколка. Один из осколков, двигаясь по вертикали вниз, упал на землю через время t₁ после взрыва. Два других упали одновременно через время t₂. Найти высоту, на которой разорвался снаряд.

 

Задача 7.53

С какой горизонтальной скоростью должен лететь снаряд массой m = 10 кг, чтобы при ударе о покоящееся судно массой М = 100 т последнее получило скорость v = м/с? Удар снаряда о судно считать неупругим.

 

Задача 7.54

На горизонтальных рельсах стоит платформа с песком общей массой М = 5 т. В песок попадает снаряд, летевший вдоль рельсов и застрявший в нем. В момент попадания снаряда его скорость равна v = 400 м/с и направлена сверху вниз под углом α = 37⁰ к горизонту. Определить скорость, приобретенную платформой, если масса снаряда равна m = 10 кг.

 

Задача 7.55

Два тела движутся навстречу друг другу с одинаковыми скоростями. После столкновения они стали двигаться вместе со скоростью u = 2 м/с. С какой скорость v тела двигались до удара, если масса одного тела больше массы другого в n = 4 раза?

 

Задача 7.56

На вагонетку массой М = 800 кг, движущуюся горизонтально со скоростью v = 20 см/с, сбросили вертикально груз массой m = 200 кг. На сколько при этом изменилась скорость вагонетки?

 

Задача 7.57

Снаряд массой m = 10 кг, летевший горизонтально со скоростью v₁ = 600 м/c, попадает в тележку с песком, имеющих общую массу М = 5 т, и застревает в песке. С какой скоростью будет двигаться тележка после попадания в нее снаряда, если она до этого имела скорость v = 1 м/с и двигалась: 1) по направлению движения снаряда; 2) навстречу движения снаряда?

 

Задача 7.58

Ракета массой М, движущаяся равномерно и прямолинейно со скоростью v, попадает в космическое тело массой m, движущееся до столкновения со скоростью и перпендикулярно направлению движения ракеты. Определить величину скорости этого тела после столкновения, если ракета застревает в нем.

 

Задача 7.59

Лыжник массой М, скользящий с горы, у которой длина спуска равна l и угол наклона к горизонту α, на половине пути стреляет из ракетницы вертикально вверх. Ракета массой m << М вылетает из ракетницы со скоростью v. Определить скорость лыжника в конце спуска. Коэффициент трения лыж о снег равен µ < tgα.

 

Задача 7.60

На наклонной плоскости, образующей с горизонтом угол α, лежит брусок массой М, который упором удерживается от соскальзывания. В брусок попадает и застревает в нем пуля массой m << М, летевшая со скоростью v снизу вверх вдоль наклонной плоскости. Определить время, через которое брусок вернется в исходное положение. Коэффициент трения между бруском и наклонной плоскостью равен µ < tgα.

 

Задача 7.61

Человек массой m неподвижно стоит на тележке, масса которой М. Тележка может двигаться по горизонтальной поверхности без трения. Определить скорость тележки, если человек начнет перемещаться по ней со скоростью v относительно тележки.

 

Задача 7.62

Рис. 7.10 - Покоящиеся призмы 1 и 2 начали двигаться из положения

Покоящиеся призмы 1 и 2, имеющие массы m₁ = m и m₂ = 3m, начали двигаться из положения, показанного на рисунке. В некоторый момент времени скорость призмы относительно призмы 2 равна v_ОТН = 3 м/с. Какую скорость имела в этот момент нижняя призма, если угол при ее основании α = 60⁰? Трение не учитывать.

 

Задача 7.63

С платформы, движущейся со скоростью v₂ = 9 км/ч, выстрелили из пушки по направлению движения. Масса платформы с пушкой М = 20 т, масса снаряда m = 20 кг, его начальная скорость относительно земли равна v₁ = 700 м/с. Чему равна скорость платформы после выстрела?

 

Задача 7.64

Мальчик может бросить мяч на расстояние S₀. На какое расстояние сместится мальчик, если он будет бросать мяч горизонтально с прежней силой, стоя на льду? Масса мальчика М, масса мяча m, коэффициент трения о лед µ.

 

Задача 7.65

Ствол пушки направлен под углом α = 45⁰ к горизонту. Когда колеса закреплены, скорость снаряда, масса которого в η = 50 раз меньше массы пушки, v₁ = 180 м/с. Найти скорость v₂ пушки сразу после выстрела, если колеса освободить.

 

Задача 7.66

Рис. 7.11 - Из пушки массой М, находящейся на наклонной плоскости, вылетает снаряд

Из пушки массой М, находящейся на наклонной плоскости, вылетает снаряд под углом α к плоскости и, если колеса закреплены, поднимается на высоту h над плоскостью (см. рисунок). Определить, на какое расстояние поднимется пушка вдоль наклонной плоскости, если в момент выстрела колеса освободить. Масса снаряда m << М, плоскость составляет угол β с горизонтом, коэффициент трения пушки о плоскость равен µ > tgβ. Сопротивлением пренебречь.

 

Задача 7.67

На одном из концов легкой соломинки массой М и длиной l лежащей на гладкой горизонтальной плоскости, сидит кузнечик массой m << М. С какой наименьшей по величине скоростью он должен прыгнуть, чтобы попасть на другой конец соломинки?

 

Задача 7.68

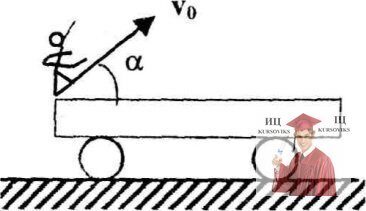
Рис. 7.12 - С какой по величине и направлению скоростью должен прыгнуть человек

С какой по величине и направлению скоростью v₀ должен прыгнуть человек массой m = 60 кг, стоящий на краю тележки массой М = 150 кг и длиной l = 1,5 м (см. рисунок), чтобы попасть на другой ее конец к моменту остановки тележки? Коэффициент трения тележки о пол µ = 0,2. Временем взаимодействия человека с тележкой пренебречь по сравнению со временем свободного полета человека. Какое расстояние пройдет тележка после того, как закончится прыжок человека?

 

Задача 7.69

Материальная точка массой m = 1 кг, двигаясь равномерно, описывает четверть окружности радиусом r = 1,2 м в течение времени t = 2 с. Найти изменение ∆р импульса точки.

 

Задача 7.70

Тело массой m = 5 кг брошено под углом α = 30⁰ к горизонту с начальной скоростью v₀ = 20 м/с. Пренебрегая сопротивлением воздуха, найти: 1) импульс силы F, действующей на тело, за время его полета; 2) изменение ∆р импульса тела за время полета.

 

Задача 7.71

Шарик массой m = 100 г упал с высоты h = 2,5 м на горизонтальную плиту, масса которой много больше массы шарика, и отскочил от нее вверх на ту же высоту. Найти импульс силы, полученный плитой.

 

Задача 7.72

Шарик массой m = 300 г ударился о стенку и отскочил от нее. Определить импульс силы, полученный стеной, если в последний момент перед ударом шарик имел скорость v₀ = 10 м/с, направленную под углом α = 30⁰ к поверхности стены. Удар считать абсолютно упругим.

 

Задача 7.73

Шарик массой m = 0,2 кг соскальзывает без трения по желобу высотой h = 2 м. Начальная скорость v₀ шарика равна нулю. Найти изменение ∆р импульса шарика и импульс р, полученный желобом при движении тела.

 

Задача 7.74

Рис. 7.13 - Неподвижная труба с площадью S поперечного сечения

Неподвижная труба с площадью S поперечного сечения, равной 10 см², изогнута под углом φ = 90⁰ и прикреплена к стене (см. рисунок). По трубе течет вода объемный расход Q_v которой 50 л/с. Найти давление р струи воды, вызванной изгибом трубы.

 

Задача 7.75

В лодке массой m₁ = 240 кг стоит человек массой m₂ = 60 кг. Лодка плывет со скоростью v₁ = 2 м/с. Человек прыгает с лодки в горизонтальном направлении со скоростью v = 4 м/с (относительно лодки). Найти скорость и движения лодки после прыжка человека в двух случаях: 1) человек прыгает вперед по движению лодки; 2) в сторону, противоположную движению лодки.

 

Задача 7.76

Две легкие тележки (массы соответственно m₁ и m₂ = 2m₁) соединены между собой сжатой, связанной нитью пружиной. Пережигая нить, пружина распрямляется и тележки разъезжаются в разные стороны. Считая коэффициент трения для обеих тележек одинаковым, определить: 1) v₁/v₂ — отношение скоростей движения тележек; 2) t₁/t₂ — отношение времен, в течение которых тележки движутся; 3) S₁/S₂ — отношение путей, пройденных тележками.

 

Задача 7.77

Две одинаковые тележки массой М каждая движется по инерции (без трения) друг за другом с одинаковой скоростью v₀. В какой-то момент времени человек массой m, находящейся на задней тележке, прыгнул в переднюю со скоростью u относительно своей тележки, Определить скорость v₁ передней тележки.

С уважением ИЦ "KURSOVIKS"!