35 Задачи с курса Физика на тему 4, Динамика движения тел по криволинейным траекториям (72 задачи) 09.11.2018 19:49

Задача 4.1

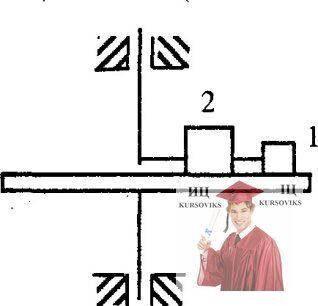
Рис. 4.1 - Гладкий горизонтальный диск равномерно вращается вокруг вертикальной оси

Гладкий горизонтальный диск равномерно вращается вокруг вертикальной оси. На поверхности диска находятся грузы 1 и 2, удерживаемые двумя нитями (см. рисунок). Масса груза 1 в два раза меньше массы груза 2, а расстояние вращения в два раза больше, чем у груза 2. Какая из нитей испытывает большую силу натяжения и во сколько раз?

 

Задача 4.2

Гладкий горизонтальный диск вращается вокруг вертикальной оси с частотой n = 480.мин^-1. На поверхности диска лежит шар массой m = 0,10 кг прикрепленный к центру диска пружиной, жесткость которой равна k = 1500 H/м. Какую длину будет иметь пружина при вращении диска. если ее длина в недеформированном состоянии l_n = 20 см?

 

Задача 4.3

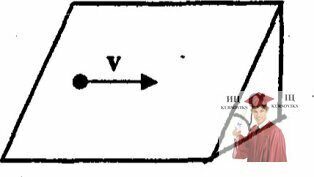
Рис. 4.2 – Монета на наклонной плоскости

На наклонной плоскости, составляющей угол α с горизонтом, лежит монета. Ей сообщили скорость v параллельно основанию наклонной плоскости (см. рисунок). Определить кривизну траектории, по которой движется монета, в начальный момент времени.

 

Задача 4.4

Рис. 4.3 - Конический маятник, состоящий из шарика, прикрепленного к нити

На рисунке изображен так называемый конический маятник, состоящий из шарика, прикрепленного к нити и описывающего окружность в горизонтальной плоскости. Масса шарика m = 100 г, длина нити l = 60 см. Найти угловую скорость шарика и силу натяжения нити.

 

Задача 4.5

Рис. 4.5 - Математический маятник имеет массу m и длину l

Математический маятник имеет массу m и длину l. В момент, когда он образует угол α с вертикалью, его скорость равна v. Какова в этот момент времени сила натяжения нити?

 

Задача 4.6

Груз, подвешенный на нити длиной l = 98 см, равномерно вращается по окружности в горизонтальной плоскости. Найти период вращения груза, если при его вращении нить отклонена от вертикали на угол α = 60⁰.

 

Задача 4.7

Рис. 4.6 - Горизонтальный вал вращается с угловой скоростью ω

Горизонтальный вал вращается с угловой скоростью ω (см. рисунок). Шарик массой т прикреплен к валу с помощью двух нитей          длиной 1. Найти силу натяжения нитей, пренебрегая силой тяжести шарика.

 

Задача 4.8

Как относятся друг к другу силы, с которыми автомобиль давит на середину выпуклого и вогнутого мостов? Радиус кривизны моста в обоих случаях равен 40 м. Скорость движения автомобиля 36 км/ч.

 

Задача 4.9

По выпуклому мосту, радиус кривизны которого R = 90 м, со скоростью v = 54 км/ч движется автомобиль массой m = 2,0 т, Определить, в какой точке сила давления автомобиля на мост равна F = 5,0 кН.

 

Задача 4.10

Самолет с реактивным двигателем летит со скоростью v = 1440 км/ч. Считая, что человек может переносить пятикратное увеличение веса, определить радиус окружности, по которой может двигаться самолет в вертикальной плоскости.

 

Задача 4.11

Поезд движется по закруглению радиусом R = 765 м со скоростью v = 72 км/ч. Определить, на сколько внешний рельс должен быть выше внутреннего. Расстояние между рельсами принять b = l,5 м.

 

Задача 4.12

С какой скоростью должен двигаться мотоциклист по гладкому треку, с углом наклона α = 30⁰ и радиусом закругления R = 90 м? С какой минимальной скоростью может двигаться мотоциклист по треку с тем же углом наклона и тем же радиусом закругления. если коэффициент трения µ = 0,40?

 

Задача 4.13

Рис. 4.7 - Шарик массой 100 г, подвешенный на легкой нити

Шарик массой 100 г, подвешенный на легкой нити, образующей угол α с вертикалью, лежит на гладкой полусфере радиусом R = 10 см (см. рисунок). Треугольник АВО прямоугольный. Шарику сообщили скорость v = 0,50 м/с перпендикулярно плоскости чертежа, и он стал скользить по полусфере, описывая окружность. Чему равна сила давления шарика на полусферу во время движения? При каком значении скорости она станет равной нулю?

 

Задача 4.14

Рис. 4.8 - Гладкий стержень наклонен под углом α = 30⁰ к горизонту

Гладкий стержень наклонен под углом α = 30⁰ к горизонту (см. рисунок) и может вращаться вокруг вертикальной оси, проходящей через нижний конец стержня О. На стержень одета бусинка, которая упирается в ограничитель на расстоянии l = 6,0 см от точки О. С какой угловой скоростью надо вращать стержень, чтобы бусинка слетела с него?

 

Задача 4.15

На краю наклонной плоскости с углом наклона α лежит тело. Плоскость равномерно вращается вокруг вертикальной оси с угловой скоростью ω. Расстояние от тела до оси вращения плоскости равно R. Найти наименьший коэффициент трения µ, при котором тело удержится на вращающейся наклонной плоскости.

 

Задача 4.16

На вертикальной оси укреплена горизонтальная штанга, по которой могут свободно перемещаться два груза с массами m₁ и m₂, связанные нитью длины 1. Система вращается с угловой скоростью ω. На каких расстояниях от оси будут находиться грузы в равновесии? Чему равна при этом сила натяжения нити? Вернутся ли грузы в состояние равновесия, если их сместить из этого положения на малое расстояние?

 

Задача 4.17

Рис. 4.9 - Шарик массой m, висящий на нити длиной l

Шарик массой m, висящий на нити длиной l, отводят в сторону в так, что нить занимает горизонтальное положение А, и отпускают без толчка. Внизу на расстоянии h = 2/3 l под точкой подвеса О вбит гвоздь С (см. рисунок). Какую силу натяжения будет иметь нить в момент, когда она займет горизонтальное положение В?

 

Задача 4.18

С какой минимальной угловой скоростью ω нужно вращать ведро в вертикальной плоскости, чтобы из него не выливалась вода? Расстояние от поверхности воды до центра вращения равно l.

 

Задача 4.19

Внутри камеры автомобильного колеса находится небольшое тело. Радиус колеса R = 0,4 м. При какой минимальной скорости автомобиля v тело будет вращаться вместе с колесом? Толщиной шины пренебречь.

 

Задача 4.20

Горизонтальный диск радиуса R = 10 м вращается вокруг своей оси с частотой n = 2 об/мин. Вдоль края диска навстречу вращению едет мотоциклист со скоростью v = 30 км/ч относительно диска. Каким должен быть коэффициент трения между шинами мотоцикла и диском, чтобы мотоцикл не соскальзывал с диска?

 

Задача 4.21

Какова должна быть скорость мотоциклиста, чтобы он мог ездить по внутренней вертикальной стенке цилиндра в горизонтальной плоскости, если известно, что при езде по горизонтальной поверхности с тем же коэффициентом трения минимальный радиус поворота на скорости равен R? Радиус цилиндра равен R₁. Под каким углом α к стенке цилиндра наклонится мотоцикл?

 

Задача 4.22

Рис. 4.10 - Две дороги АВ и CD, направленные под углом

Две дороги АВ и CD, направленные под углом α = 120⁰ друг к другу, выходят на круговую площадь радиуса R = 68 м (см. рисунок). С какой максимальной скоростью может ехать по площади автомобиль, чтобы попасть одной дороги на другую? Коэффициент трения между асфальтом и шинами автомобиля µ = 0,4.

 

Задача 4.23

Рис. 4.11 - Конечный участок горы разгона на лыжном трамплине

Конечный участок горы разгона на лыжном трамплине представляет собой дугу окружности радиуса R = 15 м (см. рисунок). Полная высота горы Н = 50 м. Найти полное ускорение прыгуна в точке В, если угол α = 30⁰. Считать, что лыжник спускается из точки А без начальной скорости. Трением пренебречь.

 

Задача 4.24

Рис. 4.12 - Один конец пружины прикреплен к гвоздю О, вбитому в стол

Один конец пружины прикреплен к гвоздю О, вбитому в стол, а другой к грузу В (см. рисунок). Груз, скользя по столу без трения, совершает круговое движение с линейной скоростью v вокруг гвоздя. Найти радиус окружности, по которой движется груз В. Массой пружины пренебречь и считать, что ее удлинение прямо пропорционально нагрузке.

 

Задача 4.25

По «экватору» внутренней поверхности сферической оболочки массы М движется шарик массой т, совершая полный оборот за время Т (с постоянной по модулю скоростью). Считая, что внешних сил нет и трение отсутствует, определить, с какой силой шарик давит на сферическую оболочку. Расстояние между центром шарика и центром сферы равно а.

 

Задача 4.26

Автомобиль начинает движение с постоянным тангенциальным ускорением а_т = 0,6 м/с ² по горизонтальной поверхности, описывая окружность радиусом R = 40 м. Коэффициент трения скольжения между колесами автомобиля и дорогой µ = 0,2. Какой путь пройдет автомобиль до начала заноса? (Под заносом будем понимать неуправляемое скольжение автомобиля на повороте в радиальном направлении).

 

Задача 4.27

Рис. 4.13 - Сферическая чаша радиуса R вращается относительно вертикального диаметра

Сферическая чаша радиуса R вращается относительно вертикального диаметра. В чаше, как показано на рисунке, находится небольшое тело. В каких пределах может меняться угловая скорость вращения, чтобы тело не соскальзывало? Угол α и коэффициент трения µ между телом и поверхностью чаши известны.

 

Задача 4.28

Каков должен быть наименьший коэффициент трения µ между шинами велосипеда и асфальтом, чтобы была обеспечена устойчивость велосипеда при движении по кривой радиуса r = 10,0 м со скоростью v = 5,0 м/с?

 

Задача 4.29

Шарик вращается в вертикальной плоскости по окружности R под действием натянутой нити. Скорость шарика в верхней точке равна v₀. Найти тангенциальное а_т и нормальное а_n, ускорения шарика как функции угла α между нитью и вертикалью (нижнему положению шарика соответствует α = 0).

 

Задача 4.30

Груз массой m, подвешенный в точке О на длинной тонкой нити длины l, массой которой можно пренебречь, совершает колебания в некоторой плоскости. Найти тангенциальное а_т и нормальное а_n ускорения груза как функции угла α. Наибольший угол отклонения нити от среднего положения равен α₀.

 

Задача 4.31

Шарик массой m = 0,100 кг, укрепленный на конце легкого стержня длины l = 1,27 м, вращается в вертикальной плоскости. В верхней точке шарик имеет скорость v₀ = 4,13 м/с. Определить силу Т, с которой шарик действует на стержень, в зависимости от α. Найти Т в верхней и нижней точках.

 

Задача 4.32

Камень, привязанный к нити, другой конец которой держат в руке, движется в вертикальной плоскости по окружности. Скорость камня в верхней точке v₁ = 4,13 м/с, в нижней точке v₂ = 6,27 м/с. Найти ускорение камня в верхней точке окружности.

 

Задача 4.33

Частица массой m со скоростью влетает в область действия тормозящей силы F под углом α < 90⁰ к линии действия этой силы. Под каким углом β к направлению силы F она вылетит из этой области? Ширина области равна l. Силой тяжести пренебречь.

 

Задача 4.34

С какой скоростью должен ехать автомобиль по выпуклому мосту с радиусом кривизны R = 10 м, чтобы не давить на его середину?

 

Задача 4.35

Автомобиль массой m = 1 т движется по эстакаде с радиусом кривизны R = 1000 м со скоростью v = 60 км/ч. Какова сила давления автомобиля на эстакаду в верхней точке?

 

Задача 4.36

Автомобиль массой m= 2 т движется по вогнутому мосту, радиус кривизны которого R = 100 м. Предельная нагрузка на мост составляет F = 22000 Н. С какой максимальной скоростью может автомобиль пересечь мост?

 

Задача 4.37

Найти силу, прижимающую летчика к сиденью самолета в нижней точке петли Нестерова, если масса летчика m = 75 кг, радиус петли R = 200 м, а скорость самолета v = 360 км/ч.

 

Задача 4.38

Груз массой m, привязанный к легкой нерастяжимой нити, вращается в вертикальной плоскости. Найти максимальную разность натяжений нити.

 

Задача 4.39

Грузик массой m = 100 г вращается на легкой нерастяжимой нити длиной l = 40 см в вертикальной плоскости. Определить силу натяжения нити в момент времени, когда угол между нитью и вертикалью равен α = 60⁰, если известно, что скорость грузика в этот момент равна v = 2 м/с.

 

Задача 4.40

На легкой нерастяжимой нити собираются вращать в вертикальной плоскости небольшое тело массой m = 1 кг. Известно, что нить выдерживает натяжение, равное Т = 50 Н. Выдержит ли нить натяжение в данном случае?

 

Задача 4.41

До какого значения должен шофер снизить скорость автомобиля на повороте радиусом R = 10 м, чтобы не возникло проскальзывание колес по поверхности дороги, если коэффициент сцепления колес автомобиля с покрытием дороги µ = 0,8?

 

Задача 4.42

Велосипедист движется по горизонтальному закруглению, отклонившись от вертикали на угол α = 22⁰. Определить возможные значения для коэффициента трения колес о поверхность дороги.

 

Задача 4.43

Определить, с какой максимальной скоростью может двигаться велосипедист по наклонному треку, не отклоняясь от нормали к дороге, если коэффициент трения между шинами и поверхностью трека µ = 0,2 Угол наклона трека к горизонт α = 45⁰, радиус закругления R = 30 м.

 

Задача 4.44

Поезд движется по закруглению дороги радиусом R = 300 м со скоростью v = 50 км/ч при расстоянии между рельсами d = 1,5 м. На сколько следует приподнять наружный рельс по отношению к внутреннему, чтобы давление на них было одинаковым?

 

Задача 4.45

Определить скорость, с которой должен двигаться мотоциклист по вертикальной цилиндрической стенке, имеющей диаметр D = 20 м, чтобы не соскользнуть вниз. Коэффициент трения принять равным µ = 0,8.

 

Задача 4.46

Сверхзвуковой самолет со скоростью v = 2000 км/ч делает поворот в горизонтальной плоскости. При каком радиусе кривизны траектории летчик будет испытывать пятикратную перегрузку? (Под перегрузкой летчика понимается отношение веса летчика к силе тяжести, действующей на негo).

 

Задача 4.47

Рис. 4.14 - Тело привязано к шнуру длиной l = 1 м

Тело привязано к шнуру длиной l = 1 м. Сколько оборотов в минуту делает тело, если шнур описывает конус, образуя с вертикалью угол α = 60⁰ (см. рисунок)?

 

Задача 4.48

Груз массой m = 1 кг, подвешен на нити длиной l = 1 м и описывает в горизонтальной плоскости окружность с постоянной угловой скоростью, совершая один оборот за секунду. Определить величину силы натяжения нити и угол, который образует нить с вертикалью.

 

Задача 4.49

Рис. 4.15 - Маленький шарик, подвешенный на невесомой нерастяжимой нити

Маленький шарик, подвешенный на невесомой нерастяжимой нити длиной l = 30 см, вращается в горизонтальной плоскости с периодом обращения Т = 1,02 с. Нить составляет с вертикалью α = 30⁰. Из этих данных найти ускорение свободного падения.

 

Задача 4.50

Груз массой m вращается на легкой нерастяжимой нити сначала в горизонтальной, а затем в вертикальной плоскостях. Определить отношение максимальных линейных скоростей вращения груза, если прочность нити Т₀ > mg.

 

Задача 4.51

Рис. 4.16 - Шарик на невесомой нерастяжимой нити

На вращающемся с угловой скоростью ω = 5 рад/с диске диаметром d = 40 см укреплен шарик на невесомой нерастяжимой нити (см. рисунок). Какой длины должна быть нить подвеса, чтобы он отклонился от вертикали на угол α = 45⁰?

 

Задача 4.52

Тело массой m подвешивают на невесомой пружине жесткостью k, длина которой в недеформированном состоянии l₀. Затем тело раскручивают, делая n оборотов за секунду так, что пружина с грузом описывает в пространстве конус. Определить возникающее при вращении удлинение пружины.

 

Задача 4.53

На диске, который может вращаться вокруг вертикальной оси, лежит маленькая шайба массой m = 100 г. Шайба соединена пружиной с осью диска. Если число оборотов диска не превышает n₁ = 2 об/с, пружина находится в недеформированном состоянии. Если число оборотов n₂ = 5 об/с, то пружина удлиняется вдвое. Определить жесткость пружины.

 

Задача 4.54

Горизонтально расположенный диск начинает раскручиваться с постоянным ускорением ε так, что угловая скорость ω = εt [рад/с], где E - известная постоянная. В какой момент времени тело, расположенное на расстоянии r от оси, начнет соскальзывать с диска, если коэффициент трения µ?

 

Задача 4.55

На гладком столе лежит кольцо массой m и радиусом R. Кольцо сделано из проволоки, выдерживающей максимальное натяжение Т₀. До какой угловой скорости нужно раскрутить кольцо, чтобы оно при движении разорвалось?

 

Задача 4.56

По внутренней поверхности полой сферы движется в горизонтальной плоскости небольшое тело. Какова должна быть скорость тела, чтобы оно при движении оставалось на высоте R/2 от нижней точки сферы? Трением пренебречь.

 

Задача 4.57

Внутрь сферы радиусом R насыпали немного песка. Где будут находиться песчинки, если сферу привести во вращение с угловой скоростью о вокруг вертикальной оси, проходящей через центр сферы? Трением песчинок о сферу пренебречь.

 

Задача 4.58

Сфера радиусом R = 2 м равномерно вращается вокруг вертикальной оси с частотой n = 3 об/с. Внутри сферы находится шарик массой m = 0,2 кг. Найти высоту h, соответствующую положению равновесия шарика относительно дна сферы, и силу реакции опоры N. Трением пренебречь.

 

Задача 4.59

Сосуд, имеющий форму усеченного расширяющегося вверх конуса с диаметром дна D = 20 см и углом наклона стенок к горизонту α = 60⁰, вращается вокруг вертикальной оси. При какой угловой скорости вращения сосуда маленький шарик, лежащий на его дне, будет выброшен из сосуда? Трением пренебречь.

 

Задача 4.60

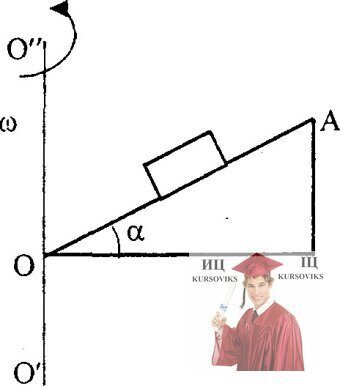
Рис. 4.17 - Наклонная плоскость ОА образует угол α с горизонтом

Наклонная плоскость ОА образует угол α с горизонтом и вращается относительно вертикальной оси O’ O'' с постоянной угловой скоростью ω (см. рисунок). На каком расстоянии от точки О тело будет находиться в равновесии, если коэффициент трения тела о плоскость µ < tgα?

 

Задача 4.61

Рис. 4.18 - Муфточка А может свободно перемещаться вдоль гладкого стержня

Муфточка А может свободно перемещаться вдоль гладкого стержня, изогнутого в форме полукольца радиусом R. Систему привели во вращение с постоянной угловой скоростью ω вокруг вертикальной оси (см. рисунок). Найти угол α, соответствующий устойчивому положению муфточки.

 

Задача 4.62

При каком отношении масс два тела, связанные нерастяжимой нитью, могут вращаться с одинаковыми угловыми скоростями на гладкой горизонтальной поверхности, если ось вращения делит нить в отношении 1:5?

 

Задача 4.63

Диск радиусом R = 40 см вращается вокруг вертикальной оси. На краю диска лежит кубик. Принимая коэффициент трения µ = 0,4, найти частоту n вращения, при которой кубик соскользнет с диска.

 

Задача 4.64

Акробат на мотоцикле описывает «мертвую петлю» радиусом r = 4 м. С какой наименьшей скоростью v_min должен проезжать акробат верхнюю точку петли, чтобы не сорваться?

 

Задача 4.65

При насадке маховика на ось центр тяжести оказался на расстоянии r = 0,1 мм от оси вращения. В каких пределах меняется сила F давления оси на подшипники, если частота вращения маховика n = 10 с^-1? Масса m маховика равна 100 г.

 

Задача 4.66

Мотоциклист едет по внутренней поверхности вертикального цилиндра радиусом R = 11,2 м. Центр тяжести мотоцикла с человеком расположен на расстоянии l = 0,8 м от поверхности цилиндра. Коэффициент трения покрышек о поверхность цилиндра равен 0,6. С какой минимальной скоростью v_min должен ехать мотоциклист? Каков будет при этом иол наклона его к плоскости горизонта?

 

Задача 4.67

Автомобиль идет по закруглению шоссе, радиус R кривизны которого равен 200 м. Коэффициент трения колес о покрытие дороги равен 0,1 (гололед). При какой скорости v автомобиля начнется его занос?

 

Задача 4.68

Какую наибольшую скорость v_max может развить велосипедист, проезжая закрепление радиусом R = 50 м, если коэффициент трения скольжения между шинами и асфальтом равен 0,3? Каков угол φ отклонения велосипеда от вертикали, когда велосипедист движется по закруглению?

 

Задача 4.69

Самолет массой m = 2,5 т летит со скоростью v = 400 км/ч. Он совершает в горизонтальной плоскости вираж (вираж - полет самолета по дуге окружности с некоторым углом крена). Радиус R траектории самолета равен 500 м. Найти поперечный угол φ наклона самолета и подъемную силу F крыльев во время полета.

 

Задача 4.70

Тонкое однородное медное кольцо радиусом R = 10 см вращается относительно оси, проходящей через центр кольца, с угловой скоростью ω = 10 рад/с. Определить нормальное напряжение δ, возникающее в кольце в двух случаях: 1) когда ось вращения перпендикулярна плоскости кольца и 2) когда лежит в плоскости кольца. Деформацией кольца при вращении пренебречь.

 

Задача 4.71

Тело массой m движется в плоскости ху по закону х = A * cosωt, y = B * sinωt, где А, В и ω - некоторые постоянные. Определить модуль силы, действующей на это тело.

 

Задача 4.72

Частица массой m движется под действием силы F = F₀ * cosωt, где F и ω некоторые постоянные. Определить положение частицы, т.е. выразить ее радиус-вектор r как функцию времени, если в начальный момент времени t = 0, r(0) = 0 и v(0) = 0.

С уважением ИЦ "KURSOVIKS"!