34 Задачи с курса Физика на тему 3, Динамика прямолинейного движения тел (65 задач) 08.11.2018 19:48

Задача 3.1

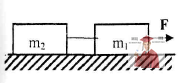
Рис. 3.1 - Два груза связаны нитью и лежат на гладкой горизонтальной поверхности

Два груза массами m₁ = 200 г и m₂ = 300 г связаны нитью и лежат на гладкой горизонтальной поверхности (см. рисунок). С каким ускорением будут двигаться грузы, если к m₁ приложить силу F = 1,5 Н, направленную параллельно плоскости стола? Какую силу натяжения будет испытывать при этом нить. связывающая тела?

 

Задача 3.2

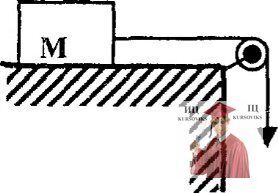
Рис. 3.2 – Тело лежит на гладком горизонтальном столе

Тело массой М = 2,0 кг лежит на гладком горизонтальном столе (см. рис.). С каким ускорением начнет двигаться тело, если: 1) нить потянуть с силой F = 9,8 Н; 2) подвесить к нити груз массой m = 1,0 кг?

 

Задача 3.3

К концам шнура, перекинутого через неподвижный блок, подвешены грузы массами m₁ = 0,10 кг и m₂ = 0,15 кг. Пренебрегая трением и считая шнур и блок невесомыми и шнур нерастяжимым, определить ускорение, с каким будут двигаться грузы, силу натяжения шнура и показания динамометра, на котором висит блок.

 

Задача 3.4

Рис. 3.3 - На штанге укреплен неподвижный невесомый блок

На штанге укреплен неподвижный невесомый блок, через который перекинута нить с двумя грузами, массы которых m₁ = 500 г и m₂ = 100 г. В грузе m₂ имеется отверстие, через которое проходит штанга (см. рисунок). Сила трения груза m₂ о штангу постоянна и равна F_тр = 13 Н. Найти ускорение а грузов и силу натяжения Т нити.

 

Задача 3.5

Через неподвижный блок, масса которого пренебрежимо мала, перекинута невесомая веревка. На одном конце веревки висит груз массы М = 25 кг, а за другой конец ухватилась обезьяна и карабкается вверх. С каким ускорением а поднимается обезьяна, если груз находится все время на одной высоте? Масса обезьяны m = 20 кг. Через какое время t обезьяна достигнет блока, если первоначально она находилась от него на расстоянии t = 20 м?

 

Задача 3.6

Рис. 3.4 - Через блок перекинута веревка

Через блок, укрепленный в вершине наклонной плоскости, перекинута веревка с двумя грузами одинаковой массы m (см. рис.). Найти силу N давления на ось, если коэффициент трения между наклонной плоскостью и лежащим на ней грузом равен µ, а угол наклона плоскости равен α. Трением в оси блока и его массой пренебречь.

 

Задача 3.7

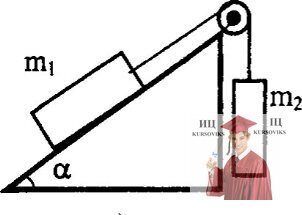
Рис. 3.5 – Груз на наклонной плоскости

Груз массы m₁ = 3 кг находится на наклонной плоскости с углом наклона α = 30⁰ и связан с грузом m₂ = 2 кг нерастяжимой легкой нитью, переброшенной через невесомый и неподвижный блок (см. рис.). Определить ускорение грузов, силу натяжения нити, силу давления на ось блока.

 

Задача 3.8

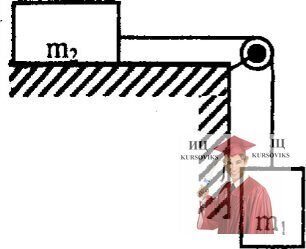
Рис. 3.6 – Брусок на горизонтальной поверхности с коэффициентом трения

На горизонтальной поверхности с коэффициентом трения µ движется брусок массой m₂, соединенный нитью со свисающим бруском массой m₁. Найти натяжение нити и силу давления на ось невесомого блока.

 

Задача 3.9

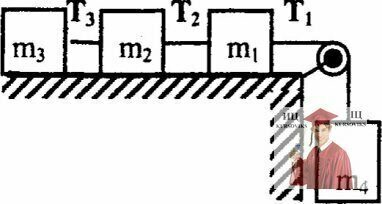
Рис. 3.7 - Три тела на горизонтальной поверхности стола

На горизонтальной поверхности стола находятся три тела с массами m₁, m₂ и m₃, связанные нитями между собой и с телом массы m₄, которое привязано к нити, перекинутой через блок (см. рис.). Коэффициент трения между телами и плоскостью стола равен µ. Найти ускорение тел а и натяжения нитей Т₁, Т₂ и T₃. Трением в блоке, а также массами блока и нитей пренебречь.

 

Задача 3.10

Рис. 3.8 - На верхнем краю наклонной плоскости

На верхнем краю наклонной плоскости, образующей угол α с горизонтом, укреплен блок, через который перекинута нить. К одному концу нити привязан груз массы m₁, лежащий на наклонной плоскости. На другом конце висит груз массы m₂ (см. рис.). Коэффициент трения между грузом и плоскостью равен µ.

1) Выяснить условия, при которых а) груз m₂ опускается; б) груз m₂ поднимается; в) грузы не двигаются. 2) Найти ускорение грузов а и натяжение нити Т для случаев (а) и (б) пункта l. Блок и нить считать невесомыми, трение в оси блока не учитывать.

 

Задача 3.11

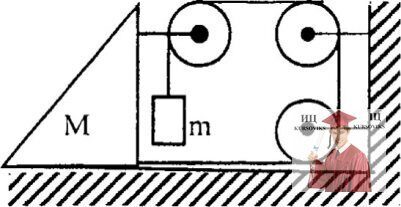
Рис. 3.9 - Ускорение грузов

Определить ускорение грузов, показанных на рисунке. Массы грузов М = 5,0 кг, m = 1,0 кг. Трением, массами блоков и нитей пренебречь.

 

Задача 3.12

Рис. 3.10 - Ускорение тел в системе

Определить ускорение тел в системе, показанной на рисунке. Коэффициент трения между телом m₁, и плоскостью равен µ = 0,10. Трением в блоке, массами блока и нити пренебречь. Масса m₁ = 1,5 кг, m₂ = 0,50 кг, сила F = 10 Н. Угол α между силой и горизонтом равен 30⁰.

 

Задача 3.13

Рис. 3.11 - Блок перекинут шнурок

Через легкий вращающийся без трения блок перекинут шнурок. На одном конце шнурка привязан груз массой m₁. По другому концу шнурка может скользить кольцо массой m₂ (см. рис.). С каким ускорением движется кольцо, если груз массой пм неподвижен? Чему равна сила трения кольца о шнурок?

 

Задача 3.14

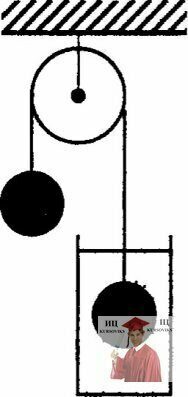
Рис. 3.12 - Два одинаковых шарика связаны невесомой нитью

Два одинаковых шарика связаны невесомой нитью, перекинутой через невесомый блок, причем один из шариков погружен в сосуд с жидкостью (см. рис.) С какой установившейся скоростью v будут двигаться шарики, если известно, что установившаяся скорость падения одиночного шарика в той же жидкости равна v₀? Сила сопротивления жидкости пропорциональна скорости. Плотность жидкости равна ρ_а, плотность материала шарика равна ρ.

 

Задача 3.15

Груз массы М = 10 кг привязан к свободно свисающему концу веревки, намотанной на лебедку. И груз, и лебедка находятся на некоторой высоте. Груз начинает падать, причем веревка натянулась, когда груз пролетел расстояние h = 12 м. После этого при помощи лебедки начали тормозить движение груза. Какую минимальную длину 1 веревки пришлось выпустить до полной остановки груза, если веревка выдерживает силу натяжения Т = 180 Н?

 

Задача 3.16

Рис. 3.13 - Два тела соединены нерастяжимой нитью

Два тела массами m₁ = 10 кг и m₂ = 1 кг соединены нерастяжимой нитью, перекинутой через блок, как показано на рисунке. Угол α = π/6, коэффициент трения между телом m₁ и наклонной плоскостью равен µ = 0,1. Найти натяжение нити, силу давления на ось блока во время движения. Наклонная плоскость неподвижна, массами блока и нити пренебречь.

 

Задача 3.17

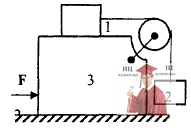
Рис. 3.14 – К системе приложить горизонтальную силу F

Какую горизонтальную силу F необходимо приложить к системе, изображенной на рисунке, чтобы тела 1 и 2 связанные нерастяжимой нитью не двигались относительно тела 3. Трение между телами 1 и 3, 2 и 3, а также между телом 3 и горизонтальной плоскостью отсутствует. Массы тел соответственно равны m₁, m₂, m₃. Задачу решить в системе отсчета, связанной с неподвижной горизонтальной плоскостью.

 

Задача 3.18

Рис. 3.15 - Два тела соединены пружиной

Два тела массами m₁ = 1 кг и m₂ = 2 кг соединены пружиной, жесткость которой k = 300 Н/м, и лежат на горизонтальной плоскости. К телу m₂ приложили силу F = 10 Н под углом α = π/6 к горизонту. Трение между телом m₁ и плоскостью отсутствует, а коэффициент трения между телом m₂ и плоскостью µ = 0,5. Найти ускорение системы и удлинение пружины в установившемся движении. Массой пружины пренебречь.

 

Задача 3.19

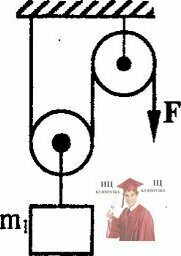
Рис. 3.16 - К оси подвижного блока подвешен груз

К оси подвижного блока подвешен груз массой m₁ (см. рис.). С какой силой F нужно потянуть конец нити, перекинутой через второй блок, чтобы груз m₁ двигался с ускорением а? Чтобы груз покоился? Чему будет равно натяжение нити в системе, если вместо силы F к свободному концу нити прикрепить груз m₂ = 3*m₁?

 

Задача 3.20

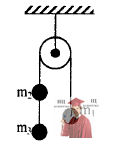
Рис. 3.17 - Натяжение нитей в системе

Определить натяжение нитей в системе, изображенной на рисунке. Блок и нити считать невесомыми, трение в оси блока не учитывать.

 

Задача 3.21

Рис. 3.18 - Гибкий канат перекинут через неподвижный блок

Гибкий канат длиной l и массой m перекинут через неподвижный блок так, что его центр масс С находится ниже от блока на расстоянии у₀ (см. рис.). Определить ускорение каната в этот момент и силу натяжения в сечении каната, проходящем через центр масс. Масса и с радиус блока пренебрежимо малы, трение отсутствует.

 

Задача 3.22

Рис. 3.19 - Ускорение грузов и натяжение нитей в системе

Определить ускорение грузов и натяжение нитей в системе, изображенной на рисунке. Массами блоков и нитей пренебречь, нити нерастяжимы. Массы m₁, m₂ и m₃ заданы.

 

Задача 3.23

К грузу массы m₁ = 7 кг подвешен на веревке груз массы m₂ = 5 кг. Масса веревки m = 4 кг. К грузу m₁ приложена направленная вверх сила F = 188,8 Н. Найти силу натяжения в верхнем конце и в середине веревки.

 

Задача 3.24

Два груза, лежащие на гладком горизонтальном столе. связаны нерастяжимой нитью. Чему равны массы грузов, если при приложении к одному из тел горизонтальной силы F = 120 Н, ускорение системы составляет а = 2 м/с, а натяжение нити равно Т = 40 Н?

 

Задача 3.25

Два груза массами m₁ = 6 кг и m₂ = 8 кг, лежащие на гладком горизонтальном столе, связаны нерастяжимой нитью. С какой силой надо тянуть груз массой m₁ в горизонтальном направлении, чтобы натяжение нити составляло Т = 60 Н?

 

Задача 3.26

Два связанных невесомой нерастяжимой нитью тела массами m₁, m₂ (m₁ < m₂) лежат на гладком горизонтальном столе. Найти натяжение нити, если сила F, параллельная поверхности стола, приложена к: а) телу массой m₁, б) телу массой m₂.

 

Задача 3.27

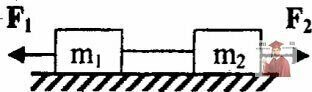
Рис. 3.20 - Два связанных невесомой и нерастяжимой нитью груза

На гладком горизонтальном столе лежат два связанных невесомой и нерастяжимой нитью груза. Масса левого груза m₁ = 200 г, масса правого m₂ = 300 г. К левому грузу приложена сила F₁ = 2 H, правому, в противоположном направлении, сила F₂= 6 Н (см. рисунок). С каким ускорением движутся грузы и какова сила натяжения соединяющей их нити?

 

Задача 3.28

Рис. 3.21 - Система n тел

Система n тел массами m₁, m₂ … m_n связанных друг с другом невесомыми нерастяжимыми нитями, движется горизонтально под действием силы F (см. рисунок). Коэффициент трения для всех тел одинаков и равен µ. Определить ускорение системы и силы натяжения всех нитей.

 

Задача 3.29

Нерастяжимый канат длиной l тянут влево с силой F₁ и вправо с силой F₂. Найти, как меняется сила натяжения каната вдоль него.

 

Задача 3.30

Мотосани массой М тянут со скоростью v₀ шесть сцепленных обычных саней массой m = M/2 каждые. В момент времени t = 0 от санного поезда отцепились двое саней. Найти закон, по которому будет меняться со временем расстояние между отцепившимися санями и остатком санного поезда. Тяга мотосаней все время постоянна. Коэффициент трения полозьев о дорогу равен µ.

 

Задача 3.31

Рис. 3.22 - Три груза соединены легкими нерастяжимыми нитями

Три груза массами m₁, m₂ и m₃ соединены легкими нерастяжимыми нитями (см. рисунок). Коэффициент трения между грузами и поверхностью стола равен µ. Определить ускорение грузов и силы натяжения нитей при движении системы. Блок невесомый, трения в оси блока нет.

 

Задача 3.32

На гладком горизонтальном столе лежат n связанных последовательно невесомыми и нерастяжимыми нитями одинаковых грузов массой m каждый. Такой же (n + 1) груз с помощью перекинутой через невесомый блок нити свешивается вниз. Определить натяжение нити между к-М и (к + 1) грузами. Трения в оси блока нет.

 

Задача 3.33

На столе лежат два шарика, соединенные пружиной. Массы шариков m₁ и m₂, жесткость пружины k. На шарик массой m₁, действует постоянная сила F по направлению к шарику массой m₂ (вдоль пружины). На какую величину сжата пружина? Трения нет, колебания отсутствуют.

 

Задача 3.34

Тела массой m₁ и m₂ лежащие на гладкой горизонтальной поверхности, соединены пружиной жесткостью k. На тело массой m₂ действует сила F, направленная вдоль пружины к телу массой m₁. Найти, на сколько сжата пружина, если никаких других сил нет, а колебания уже прекратились. Какими будут ускорения тел сразу после прекращения действия силы?

 

Задача 3.35

Рис. 3.23 - Два бруска скрепленные недеформированной пружиной

Два бруска массой m₁ и m₂, скрепленные недеформированной пружиной жесткостью k, находятся на гладком горизонтальном столе. К брускам приложили горизонтальные силы F₁ и F₂, направленные в противоположные стороны (см. рисунок). Найти удлинение пружины.

 

Задача 3.36

Рис. 3.24 - (n+l) одинаковых грузов массой m каждый соединены друг с другом

(n+l) одинаковых грузов массой m каждый соединены друг с другом n одинаковыми невесомыми пружинами. К крайнему грузу приложена некоторая сила F, под действием которой система движется с ускорением а в горизонтальном направлении (см. рисунок). Определить величину силы F и удлинение ∆х, каждой пружины, если коэффициент трения между грузами и плоскостью равен µ, а жесткость каждой пружины равна k.

 

Задача 3.37

Два небольших тела массой m₁ = 2 кг и m₂ = 1 кг связаны невесомой и нерастяжимой нитью и расположены на горизонтальной плоскости. К первому телу приложена сила F = 10 Н, направленная под углом α = 30⁰ к горизонту (вверх). Определить ускорение системы, если коэффициент трения тел о плоскость одинаков и равен µ = 0,1.

 

Задача 3.38

Два одинаковых груза массой М = 0,24 кг каждый связаны невесомой нерастяжимой нитью, перекинутой через невесомый, блок с неподвижной осью. На один из грузов кладут перегрузок массой m = 10 г и вся система приходит в движение. Определить, какой путь пройдут грузы за первые t = 4 с движения. Трения в оси блока нет.

 

Задача 3.39

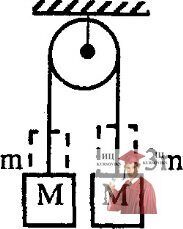
Рис. 3.25 - Через легкий блок перекинута невесомая нерастяжимая нить

Через легкий блок перекинута невесомая нерастяжимая нить, на концах которой висят два одинаковых груза массой М каждый (см. рисунок). Одновременно на каждый из этих грузов кладут по перегрузку: справа массой 3m и слева массой m. Определить ускорение системы и натяжение нити. Трения в оси блока нет.

 

Задача 3.40

Рис. 3.26 - Через неподвижный блок перекинута нерастяжимая нить

Через неподвижный блок перекинута нерастяжимая нить, к которой подвешены пять грузов одинаковой массы m, как показано на рисунке. Определить ускорение грузов и силы натяжения всех нитей. Массой блока пренебречь. Трения нет.

 

Задача 3.41

Рис. 3.27 - Невесомая и нерастяжимая нить, перекинутая через легкий блок

Невесомая и нерастяжимая нить, перекинутая через легкий блок с неподвижной осью вращения, пропущена через муфту (см. рисунок). При движении нити на нее со стороны муфты действует постоянная сила трения F. На концах нити подвешены грузы массами m₁ и m₂ (m₁ > m₂). Определить ускорение грузов. Трения в оси блока нет.

 

Задача 3.42

Рис. 3.28 – Движение груза в установке

Определить ускорение, с которым движется груз m₁ в установке, изображенной на рисунке. Масса груза m₂ = 4m₁. Трением, массами блоков и нити, а также растяжением нити пренебречь.

 

Задача 3.43

Считая блоки невесомыми, найти скорость груза (см. рисунок к задаче 3.42) в момент, когда он прошел расстояние s. Начальные скорости грузов равны нулю. Трения нет. Нить невесома и нерастяжима.

 

Задача 3.44

Рис. 3.29 - Груз массой m = 2 кг подвешен к оси легкого подвижного блока

Груз массой m = 2 кг подвешен к оси легкого подвижного блока (см. рисунок). Какую силу необходимо приложить к свободному концу нити, чтобы система находилась в равновесии? Как будет двигаться система, если к концу нити приложена сила F = 12 Н? Определить в этом случае ускорение груза и натяжение нити. Массой блока и нити пренебречь. Нить нерастяжима, трения в оси блока нет.

 

Задача 3.45

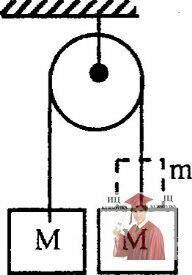
Рис. 3.30 - Сила давления грузика m на груз М во время движения системы грузов

Найти силу давления грузика m на груз М во время движения системы грузов, изображенной на рисунке. Нить, связывающая грузы, невесома и нерастяжима. Массу блока не учитывать, трения нет.

 

Задача 3.46

Через легкий блок перекинута невесомая нерастяжимая веревка, по обоим концам которой с ускорениями а₁ и а₂ относительно веревки поднимаются две обезьяны. Определить силу натяжения веревки, если массы обезьян равны соответственно m₁ и m₂. Трения в оси блока нет.

 

Задача 3.47

Нить перекинута через легкий, вращающийся без трения блок. На одном конце нити прикреплен груз массой М, а по другой свисающей части нити скользит муфточка массой m с постоянным ускорением а относительно нити. Найти силу трения, с которой нить действует на муфточку.

 

Задача 3.48

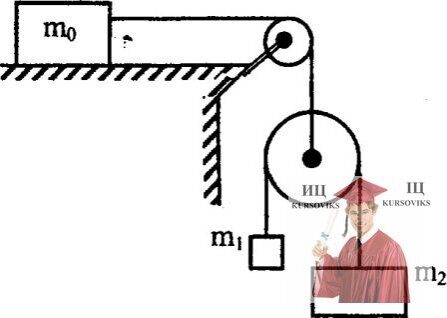
Рис. 3.31 - Массы тел равны m₀, m₁, m₂

В системе, показанной на рисунке, массы тел равны m₀, m₁, m_2, трения нет. Найти ускорение тела

 

Задача 3.49

Вверх по наклонной плоскости с углом наклона α при основании тянут с ускорением а однородный трос длиной l и массой М. Коэффициент трения между тросом и плоскостью µ. Найти натяжение троса в сечении, находящемся на расстоянии х от его верхнего конца.

 

Задача 3.50

Рис. 3.32 - Два кубика, находящиеся на наклонных плоскостях

Два кубика, находящиеся на наклонных плоскостях, связаны невесомой нерастяжимой нитью, перекинутой через невесомый блок. Наклонные плоскости образуют с горизонтальной плоскостью углы α и β (см. рисунок). Массы кубиков равны m₁ и m₂. Коэффициент трения о плоскость для обоих кубиков один и тот же. Какому условию должен удовлетворять этот коэффициент, чтобы движение кубиков было ускоренным? Трения в оси блока нет.

 

Задача 3.51

Рис. 3.33 - Грузы массами m₁ = 1 кг и m₂ = 2 кг лежат на горизонтальной плоскости

В системе, изображенной на рисунке, грузы массами m₁ = 1 кг и m₂ = 2 кг лежат на горизонтальной плоскости. Нить, соединяющая грузы, невесома и нерастяжима. Блоки невесомы, трения в осях блоков нет. Коэффициенты трения грузов о плоскость соответственно µ₁ = 0,5 и µ₂ = 0,2. В момент времени t₀ = 0 на ось верхнего блока начинает действовать сила F = 12 H, направленная вертикально вверх. На сколько сблизятся грузы за время t = 0,4 с после начала действия силы? Как изменится ответ, если сила F = 9 Н?

 

Задача 3.52

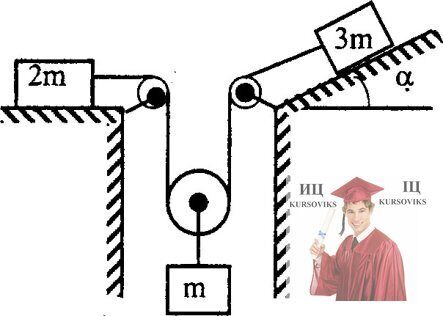
Рис. 3.34 - Сила натяжения нити и ускорение связанных между собой грузов

Определить силу натяжения нити и ускорения связанных между собой грузов (см. рисунок). Наклонная плоскость составляет с горизонтом угол α = 30⁰. Массой блоков и трением пренебречь, нити считать невесомыми и нерастяжимыми.

 

Задача 3.53

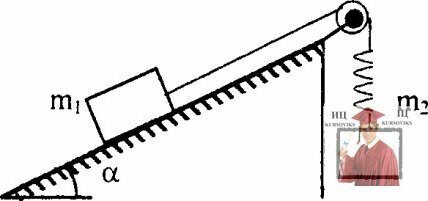
Рис. 3.35 - Массы тел равны m₁ и m₂

Массы тел, изображенных на рисунке, равны m₁ и m₂, коэффициент трения первого груза о плоскость µ, угол наклона плоскости призмы α. Тела соединены через невесомый         блок без трения невесомой нерастяжимой нитью и жесткостью k. Определить величину деформации пружины. Призма неподвижна.

 

Задача 3.54

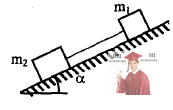
Рис. 3.36 - Два тела массой m₁ и m₂, соединенные невесомой нерастяжимой нитью

Два тела массой m₁ и m₂, соединенные невесомой нерастяжимой нитью, удерживаются на наклонной плоскости с углом при основании α (см. рисунок). Коэффициенты трения тел о плоскость равны µ₁ и µ₂ соответственно, причем µ₁ > tgα, µ₂ < tgα. Найти силу натяжения нити, если тела отпустить.

 

Задача 3.55

Рис. 3.37 - Два тела массой m₁ и m₂ соединенные невесомой недеформированной пружиной жесткостью k

Два тела массой m₁ и m₂ соединенные невесомой недеформированной пружиной жесткостью k, удерживаются на наклонной плоскости с углом при основании α (см. рисунок). Коэффициенты трения тел о плоскость равны µ₁ и µ₂ ответственно, причем µ₁ < tgα, µ₂ > tgα. Найти установившееся изменение длины пружины, если тела опустить.

 

Задача 3.56

Рис. 3.38 - Тело массой m₁ соединено легкой пружиной жесткостью k

Тело массой m₁, находящееся на горизонтальном столе, соединено легкой пружиной жесткостью k и невесомой нерастяжимой нитью с телом массой m₂ так, как показано на рисунке. Найти установившееся изменение длины пружины, если стол начнет двигаться горизонтально с ускорением а. Коэффициент трения тела массой m₁, о поверхность стола равен µ. Задачу решать в инерциальной системе отсчета.

 

Зaдача 3.57

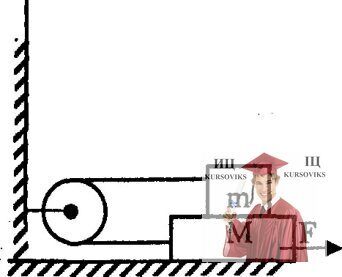
Рис. 3.39 - На гладком горизонтальном столе лежит брусок массой М = 2 кг

На гладком горизонтальном столе лежит брусок массой М = 2 кг, на котором находится брусок массой m = 1 кг (см. рисунок). Какую силу надо приложить к нижнему бруску, чтобы он двигался с постоянным ускорением а = 5 м/с²? Коэффициент трения между брусками равен µ = 0,5. Нить невесома и нерастяжима.

 

Задача 3.58

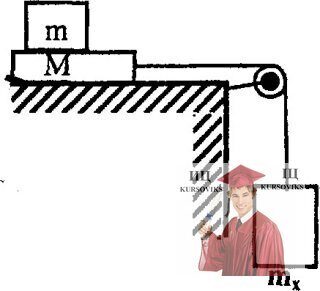
Рис. 3.40 - Доска массой М может скользить без трения по горизонтальной поверхности

Доска массой М может скользить без трения по горизонтальной поверхности. На доске лежит брусок массой m. Коэффициент трения между поверхностями бруска и доски равен µ. Доска соединена с грузом перекинутой     через невесомый блок нерастяжимой нитью (см. рисунок). Какой должна быть масса груза m_х, чтобы брусок скользил по доске?

 

Задача 3.59

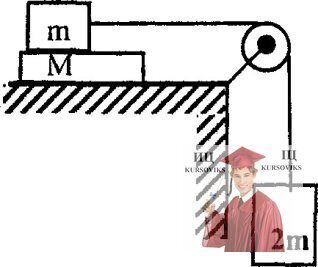
Рис. 3.41 - На гладком горизонтальном столе лежит доска массой М = 2 кг

На гладком горизонтальном столе лежит доска массой М = 2 кг, на которой находится брусок массой m = 1 кг. Брусок соединен невесомой нерастяжимой нитью перекинутой через невесомый блок, с грузом массой 2 m (см. рисунок). С каким ускорениями будут двигаться тела, предоставленные       самим себе, коэффициент трения между поверхностями бруска и доски равен µ?

 

Задача 3.60

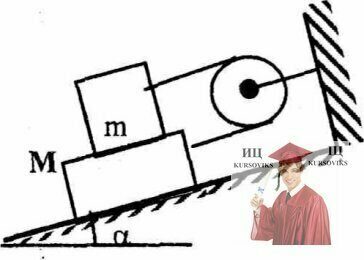
Рис. 3.42 - Доска массой М на наклонной плоскости

На наклонной плоскости с углом при основании α = 60⁰ лежит доска массой М, на доске — брусок массой m = 2,3 кг. Брусок и доска соединены между собой с помощь невесомой нерастяжимой нити, перекинуто! через невесомый блок, как показано н рисунке. Коэффициент трения между поверхностями бруска и доски µ₁ = 0,2 кг, доски и плоскости - µ₂ = 0,4. При каких значениях массы доски М брусок будет двигаться вниз?

 

Задача 3.61

Рис. 3.43 - Брусок А перемещать в горизонтальном направлении

С каким минимальным ускорением нужно перемещать в горизонтальном направлении брусок А, чтобы тела 1 и 2 не двигались относительно бруска? Массы тел и 2 равны. Коэффициент трения между бруском и обоими телами равен µ. Задачу решать в системе отсчета, связанной с неподвижной горизонтальной плоскостью.

 

Задача 3.62

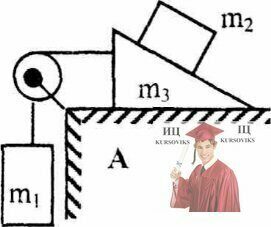
Рис. 3.44 - Ускорение тел массой m₁, m₂ и m₃ в механической системе

Определить ускорения тел массой m₁, m₂ и m₃ в механической системе, показанной на рисунке. Массой блока и нити, а также трением в оси блока и между поверхностями пренебречь. Нить нерастяжима. Задачу решать в системе отсчета, связанной с неподвижной поверхностью стола А.

 

Задача 3.63

К пружинным весам подвешен блок. Через блок перекинут шнур, к концам которого привязали грузы массами m₁ = 1,5 кг и m₂ = 3 кг. Каково будет показание весов во время движения грузов? Массой блока и шнура пренебречь.

 

Задача 3.64

На гладком столе лежит брусок массой m = 4 кг. К бруску привязаны два шнура, перекинутые через неподвижные блоки, прикрепленные к противоположным краям стола. К концам шнуров подвешены гири, массы которых m₁ = 1 кг и m₂ = 2 кг. Найти ускорение а, с которым движется брусок, и силу натяжения каждого из шнуров. Массой блоков и трением пренебречь.

 

Задача 3.65

Ракета, масса которой М = 6 т, поднимается вертикально вверх. Двигатель ракеты развивает силу тяги F = 500 кН. Определить ускорение а ракеты и силу натяжения Т троса, свободно свисающего с ракеты, на расстоянии, равном 1/4 его длины от точки прикрепления троса. Масса m троса равна 10 кг. Силой сопротивления воздуха пренебречь.

С уважением ИЦ "KURSOVIKS"!