33 Задачи с курса Физика на тему 2, Динамика движения тел по прямым траекториям (132 задачи) 08.11.2018 19:39

Задача 2.1

С какой силой давит человек массой m = 70 кг на пол лифта, движущегося с ускорением 0,8 м/с²: 1) вверх; 2) вниз? С каким ускорением должен двигаться лифт, чтобы человек не давил на пол?

 

Задача 2.2

Для задачи 2.1 вычислить силу натяжения каната, удерживающего лифт при подъеме: 1) ускоренном; 2) равномерном; З) замедленном. Масса лифта 300 кг.

 

Задача 2.3

Рис. 2.1 - Горизонтальная плоскость

На горизонтальной плоскости лежат четыре кирпича с массой m = 2,00 кг каждый. Сила F = 46 Н действует, как показано на рисунке. Найти результирующую силу f, действующую на каждый кирпич. Коэффициент трения µ = 0,50. С какой силой f второй кирпич действует на третий?

 

Задача 2.4

Тело массой m = 1,0 кг лежит на горизонтальной плоскости. Коэффициент трения µ = 0,10. На тело действует горизонтальная сила F. Определить силу трения для двух случаев: 1) F = 0,50 Н; 2) F = 2,0 Н. Изобразить графически, как меняется сила трения при изменении силы F.

 

Задача 2.5

Брусок находится на наклонной плоскости, угол наклона которой может меняться от 0 до 90⁰. Построить график зависимости силы трения бруска о плоскость от угла наклона плоскости к горизонту, Коэффициент трения равен µ. Как с помощью такой плоскости определять коэффициент трения между плоскостью и различными телами?

 

Задача 2.6

Тело массой m, находящееся на горизонтальной плоскости, тяни с силой F < mg, направленной под углом α к горизонту. Коэффициент трения между телом и плоскостью µ. Построить график зависимости силы трения от угла α между силой и вертикалью.

 

Задача 2.7

На тело массой m = 1,0 кг. находящееся на горизонтальной плоскости, действует горизонтальная сила F = 3,0 Н. С какой минимальной горизонтальной силой F_min надо подействовать в перпендикулярном к силе F направлении, чтобы тело начало скользить? Коэффициент трения тела о плоскость µ = 0,50.

 

Задача 2.8

Рис. 2.2 - Брусок массой m = 0,50 кг лежит на шероховатой поверхности

Брусок массой m = 0,50 кг лежит на шероховатой поверхности (см. рис.), наклоненной к горизонту под углом α = 30⁰ С какой минимальной горизонтальной силой F, параллельной ребру АВ двугранного угла, следует потянуть за нить, привязанную к бруску, чтобы началось его скольжение? Коэффициент трения бруска о поверхность µ = 0,70.

 

Задача 2.9

Рис. 2.3 - Два бруска одинаковой массы на наклонной плоскости

Два бруска одинаковой массы m = 0,2 кг поставили на наклонную плоскость с углом наклона α = 45⁰ (см. рисунок). Коэффициент трения верхнего бруска о плоскость µ₁ = 0,01, нижнего µ₂ = 1. Определить силу взаимодействия брусков при их совместном соскальзывании с наклонной плоскости.

 

Задача 2.10

Рис. 2.4 - Призма массы М с углом наклона α

На гладком горизонтальном столе лежит призма массы М с углом наклона α, а на ней призма массы m (см. рис.). На меньшую призму действует горизонтальная сила F, при этом обе призмы движутся вдоль стола как одно целое (т.е. не изменяя взаимного расположения). Определить силу трения между призмами.

 

Задача 2.11

Брусок массой m = 3,0 кг с помощью пружины тянут равномерно по доске, расположенной горизонтально. Какова жесткость пружины, если она удлинилась при этом на l = 5,0 см? Коэффициент трения бруска о плоскость µ = 0,25.

 

Задача 2.12

Какова начальная скорость шайбы, пущенной по поверхности льда, если она остановилась через 40 с? Коэффициент трения шайбы о лед µ = 0,05.

 

Задача 2.13

Определить ускорение тела, соскальзывающего с наклонной плоскости, если ее угол наклона α = 30⁰, а коэффициент трения между телом и наклонной плоскостью µ = 0,30.

 

Задача 2.14

Человек потянул санки массой m = 8 кг с силой F = 100 Н за веревку под углом α = 30⁰ к горизонту. Коэффициент трения санок о снег µ = 0,10. Определить ускорение, с которым начнут двигаться санки.

 

Задача 2.15

Рис. 2.5 - Вагонетка массой М = 500 кг опускается по наклонной дороге

По наклонной дороге с углом наклона α = 30⁰ к горизонту (см. рис.) опускается вагонетка массой М = 500 кг. Определить силу натяжения каната при торможении вагонетки в конце спуска, если ее скорость перед торможением была vo = 2 м/с, а время торможения t = 0,5 с. Коэффициент трения принять равным µ = 0,010.

 

Задача 2.16

Доска массой М может двигаться без трения по наклонной плоскости с углом α к горизонту. В каком направлении и с каким ускорением должна бежать по доске собака массой m, чтобы доска не соскальзывала с наклонной плоскости?

 

Задача 2.17

Человек скатывается на санях под уклон составляющий угол α = 6⁰ с горизонтом. Масса саней М в два раза больше массы человека m. Коэффициент трения саней о поверхность склона µ = 0,2. Как должен двигаться человек относительно саней, чтобы сани двигались под уклон равномерно?

 

Задача 2.18

Человек скатывается на санях под уклон, составляющий угол α = 30⁰ с горизонтом. Масса человека М в два раза больше массы саней т. Коэффициент трения саней о поверхность склона µ = 0,3. Как должен двигаться человек относительно саней, чтобы сани двигались под уклон равномерно?

 

Задача 2.19

Автомобиль начал двигаться с ускорением а₁ = 2,0 м/с². при скорости 70 км/ч ускорение стало равным а₁ = 1,0 м/с². Определить, с какой установившейся скоростью будет двигаться автомобиль, если сила мотора остается постоянной, а сила сопротивления пропорциональна скорости.

 

Задача 2.20

Поезд, подъезжая к станции со скоростью v = 72 км/ч, начинает тормозить. Каково наименьшее время торможения поезда до полной остановки, безопасное для спящих пассажиров ( пассажиры не падают с полок )? Коэффициент трения о полки µ = 0,2.

 

Задача 2.21

Длина взлетной полосы самолета L = 1 км, скорость при взлете v = 200 км/ч. Какую перегрузку испытывает пассажир в этом самолете, если разгон происходит равноускоренно?

 

Задача 2.22

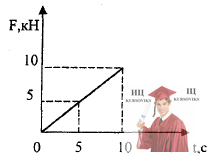
Рис. 2.6 - Автомобиль движется со скоростью

Автомобиль массой m = 2*10³ кг движется со скоростью v = 90 км/ч. В момент времени t = 0 на него начинает действовать тормозящая горизонтальная сила F, которая нарастает со временем по линейному закону (см. рисунок). Через какое время автомобиль остановится?

 

Задача 2.23

При скоростном спуске лыжник шел вниз по склону с углом наклона φ = 45⁰ не отталкиваясь палками. Коэффициент трения лыж о снег µ = 0,1. Сила сопротивления воздуха пропорциональна квадрату скорости: F = α*v², где постоянная величина α = 0,7 кг/м. Какую максимальную скорость мог развить лыжник, если его масса m = 90 кг?

 

Задача 2.24

Парашютист массы m₁ = 80 кг падает при открытом парашюте с установившейся скоростью v₁ = 5 м/с. Какой будет установившаяся скорость, если на том же парашюте спускается мальчик массы m₂ = 40 кг? Сила сопротивления воздуха пропорциональна квадрату скорости.

 

Задача 2.25

От поезда, идущего по горизонтальному участку пути с постоянной скоростью v₀, отделяется 1/3 состава. Через некоторое время скорость отцепившихся вагонов уменьшилась в два раза. Считая, что сила тяги при разрыве состава не изменилась, определить скорость головной части поезда в этот момент. Сила трения пропорциональна силе тяжести и не зависит от скорости.

 

Задача 2.26

Тело движется под действием силы F = 80 Н. Определить массу тела, если известно, что от состояния покоя до начала равномерно ускоренного движения прошло 10 секунд и путь тела за этот промежуток изменялся в зависимости от времени по закону s = bt² + ct², где b = 1 м/с², с = 0,1 м/с³. Найти также силу, которая действовала на тело через 5 секунд после начала движения.

 

Задача 2.27

Тело, имеющее постоянную массу, до начала торможения двигалось равномерно, а в момент остановки тормозящая сила достигла значения F_ост = 40 Н. Определить тормозящую силу через 3 секунды после начала торможения, если тормозной путь, в зависимости от времени, изменялся по закону s = ct - bt^3, где с = 196 м/с и b = 1 м/с³.

 

Задача 2.28

Железнодорожная платформа массой m = 2*10⁴ кг движется со скоростью v₁ = 30 км/ч. Определить среднее значение силы, действующей на платформу для трех случаев остановки платформы: 1) при встрече с неподвижным препятствием в течение 0,8 с; 2) при торможении в течение 10 с; 3) под влиянием сил трения в течение 10 мин.

 

Задача 2.29

Для тела массой 5 кг путь до полной остановки в зависимости от времени выражен в первом случае уравнением х₁ =b₁t – c₁t² и во втором случае х₂ = b₂t² – c₂t³, где b₁ = 40 м/с, c₁ = 4 м/c², b₂ = 12 м/c², c₂ = 1,6 м/c³. Найти в обоих случаях время и путь до полной остановки. а также построить график зависимости силы от времени на заданном отрезке пути.

 

Задача 2.30

Тело массой m движется под действием постоянной силы F. В момент времени t = t₀ тело было в точке х = х₀. Найти, какую скорость должно иметь тело при t = t₀, чтобы в момент времени t = t_k попасть в точку с координатой х = x_k.

 

Задача 2.31

Разрывное усилие троса подъемного крана 5*10⁴ Н. При каком ускорении произойдет разрыв троса, если поднимать груз массой 3 т?

 

Задача 2.32

Человек весом Р = 750 Н стоит на пружинных весах в кабинете лифта, движущегося с ускорением а = 5 м/с². Что покажут весы, когда лифт движется: а) вверх; б) вниз?

 

Задача 2.33

Вагонетку массой 400 кг тянут с постоянной скоростью на подъем высотой 40 м и длиной 200 м. Вычислить силу, которая потребуется для подъема, если она направлена: а) параллельно подъему; б) горизонтально. Трением пренебречь.

 

Задача 2.34

Рис. 2.7 - Брусок массой m тянут за нить

Брусок массой m тянут за нить так, что он движется с постоянной скоростью по горизонтальной плоскости (см. рис.). Коэффициент трения между телом и плоскостью равен µ. Найти угол α, при котором натяжение нити будет наименьшим.

 

Задача 2.35

Тело массой m = 1кг лежит на горизонтальной плоскости. К телу приложили силу F, направленную под углом α к горизонту (см. рис. к задаче 2.34). Коэффициент трения между поверхностью тела и плоскостью равен µ. Определить ускорение тела в следующих случаях:а) α = 0, µ = 0,2, F = 0,5H; 2H; 2,5H; б) α=π/6, µ = 0,2, F = 4Н.

 

Задача 2.36

Брусок массой m = l кг находится на наклонной плоскости, угол между которой и горизонтом может меняться: 0 ≤ α ≤. π/2. Начертить графики зависимости силы трения и ускорения бруска от угла L, если коэффициент трения между бруском и плоскостью µ = 0,5.

 

Задача 2.37

Шар массой m лежит на ящике, соскальзывающем с наклонной плоскости, образующей угол α с горизонтом. Найти силы, с которыми шар давит на дно и переднюю стенку ящика. Рассмотреть два случая: 1) трение между ящиком и наклонной плоскостью отсутствует; 2) коэффициент трения между ящиком и наклонной плоскостью равен µ.

 

Задача 2.38

Предмет, брошенный вперед по льду со скоростью 10 м/с, проходит путь, равный 50 м. Через сколько минут он остановится?

 

Задача 2.39

Ящик массой 60 кг тянут равномерно по полу с помощью веревки, прикрепленной к ящику. Веревка образует угол 30⁰ с полом. Коэффициент трения между ящиком и полом равен 0,4. Определить силу, под действием которой движется ящик.

 

Задача 2.40

Автомобиль движется со скоростью 50 км/ч. Коэффициент трения между шинами и дорогой равен 0,75. Определить минимальное расстояние, на котором машина может быть остановлена.

 

Задача 2.41

Тело массой m поднимают по наклонной плоскости с ускорением а. Какую силу, параллельную наклонной плоскости, необходимо приложить для подъема тела? Коэффициент трения соприкасающихся поверхностей µ = 0,2, угол наклона α = 30⁰.

 

Задача 2.42

Сейф массой 10 т должен быть погружен на грузовик высотой 1,5 м с помощью досок длиной 6 м. Определить наименьшую силу, необходимо для передвижения сейфа, если коэффициент трения µ = 0,35.

 

Задача 2.43

Аэростат массой m = 250 кг начал опускаться с ускорением a = 0,2 м/c². Определить массу балласта, которым следует сбросить. Чтобы аэростат получил такое же ускорение, но направленное вверх.

 

Задача 2.44

Тело массой m = 2 кг падает вертикально вниз с ускорением а = 9 м/с². Определить среднее значение силы сопротивления воздуха.

 

Задача 2.45

Тело массой m = 10 кг поднимается вертикально вверх на высоту h = 20 м под действием постоянной силы F = 196 Н. Чему равна конечная скорость тела? Сопротивлением среды пренебречь.

 

Задача 2.46

Тело массой m = 0,4 кг бросают вертикально вверх с начальной скоростью v₀ = 30 м/с. Через τ = 2,5 с тело достигает высшей точки подъема. Определить среднее значение силы сопротивления воздуха, считая, что движение было равнозамедленным.

 

Задача 2.47

Через сколько секунд тело, брошенное вертикально вверх со скоростью v₀ = 44,8 м/с, упало на Землю, если сила сопротивления воздуха не зависит от скорости и составляет η = 1/7 силы тяжести?

 

Задача 2.48

Воздушный шар опускается с постоянной скоростью. Сколько килограммов балласта нужно сбросить, чтобы шар начал подниматься с такой же скоростью? Масса шара М, подъемная сила F постоянна.

 

Задача 2.49

Вертикально стартующая ракета развивает силу тяги F в течение времени t, затем двигатель отключается. Определить, через какое время т после старта ракета вернется на Землю. Масса ракеты М, ее изменением пренебречь. Сопротивление воздуха и изменение ускорения свободного падения с высотой не учитывать.

 

Задача 2.50

На нити, выдерживающей натяжение F₀ = 20 Н, поднимают груз массой m = 1 кг из состояния покоя вертикально вверх. Считая движение равноускоренным, найти предельную высоту, на которую можно поднять груз за τ = 1 с так, чтобы нить не оборвалась.

 

Задача 2.51

Стальная проволока некоторого диаметра выдерживает натяжение до F₀ = 4400 Н. С каким наибольшим ускорением можно поднимать груз массой m = 400 кг, подвешенный на этой проволоке, чтобы при этом она не разорвалась?

 

Задача 2.52

Груз массой m поднимают при помощи троса вертикально вверх. В течение первых секунд равноускоренного движения груз поднят на высоту h. Определить удлинение троса, если его коэффициент упругости k. Деформацию считать упругой. Массу троса и сопротивление среды не учитывать.

 

Задача 2.53

Автомобиль, трогаясь с места, за τ = 5 с равно ускоренно набирает скорость v = 72 км/ч. Найти минимально возможный коэффициент трения между колесами автомобиля и дорогой при таком движении. Каков наименьший тормозной путь автомобиля, набравшего эту скорость?

 

Задача 2.54

Как изменится скорость тела массой m = 5 кг, движущегося со скоростью v₀ = 8 м/с, если на пути s = 10 м на тело будет действовать постоянная тормозящая сила, равная F = 12 Н?

 

Задача 2.55

На тело массой m = 5 кг, движущееся со скоростью v₀ = 6 м/с, начинает действовать сила F = 8 Н, направленная в сторону, противоположную движению. В результате скорость тела уменьшается до v = 2 м/с. Какой путь прошло тело за время действия силы?

 

Задача 2.56

Мотоциклист, движущийся со скоростью v = 70,6 км/ч, начинает тормозить. Через τ = 5 с после начала торможения он останавливается. Чему равен средний коэффициент трения колес мотоцикла о покрытие дороги во время торможения?

 

Задача 2.57

Автомобиль массой m = 1 т, двигаясь равнозамедленно, останавливается через τ = 5 с, пройдя путь s = 25 м. Найти начальную скорость автомобиля и силу торможения.

 

Задача 2.58

Поезд массой m = 500 т, двигаясь равнозамедленно, в течение времени τ = 1 мин уменьшает свою скорость от v₀ = 40 км/ч до v = 28 км/ч. Найти среднюю силу торможения.

 

Задача 2.59

Определить, с какой скоростью двигался автомобиль, если длина следа заторможенных колес оказалась равной s = 25 м. Коэффициент трения покрышек о покрытие дороги µ = 0,3.

 

Задача 2.60

Определить отношение максимально возможных расстояний, которые преодолевает шайба, брошенная по льду (коэффициент трения µ = 0,1) и брошенная с той же скоростью под углом к горизонту.

 

Задача 2.61

Чему должен быть равен минимальный коэффициент трения u между шинами и поверхностью наклонной дороги, чтобы автомобиль с включенным двигателем мог двигаться по ней вверх с ускорением а = 0,5 м/с² ? Угол наклона дороги α = 30⁰.

 

Задача 2.62

Небольшое тело въезжает на наклонную плоскость, имея скорость v₀ = 19,6 м/с. Через τ = 4 с движения по наклонной плоскости тело останавливается. Чему равен угол наклона плоскости к горизонту? Трением пренебречь.

 

Задача 2.63

Тело скользит по наклонной плоскости, составляющей с горизонтом угол α = 45⁰. Пройдя путь s = 36,4 см, тело приобретает скорость v = 2 м/с. Найти коэффициент трения тела о плоскость.

 

Задача 2.64

Какой путь пройдут сани по горизонтальной поверхности после спуска с горы высотой h = 15 м, имеющей угол наклона к горизонту α = 30⁰? Коэффициент трения полозьев о снег µ = 0,2.

 

Задача 2.65

Ледяная горка составляет с горизонтом угол α = 30⁰. По ней пускают снизу вверх камень, который за время t = 2 с проходит расстояние s = 16 м, после чего скатывается вниз. Найти коэффициент трения между поверхностью горки и камнем, а также время соскальзывания.

 

Задача 2.66

Небольшое тело пустили снизу вверх по наклонной плоскости, составляющей угол α с горизонтом. Коэффициент трения тела о плоскость равен µ. Определить отношение времени подъема тела t₁ вверх ко времени его соскальзывания t₂ вниз до первоначальной точки.

 

Задача 2.67

Небольшое тело пустили снизу вверх по наклонной плоскости, составляющей угол α = 15⁰ с горизонтом. Найти коэффициент трения, если время подъема тела оказалось в n = 2 раза меньше времени спуска.

 

Задача 2.68

За какое время тело массой m соскользнет с наклонной плоскости длиной l и углом наклона β, если по наклонной плоскости с углом α < β, оно движется равномерно?

 

Задача 2.69

Небольшому телу, находящемуся у основания наклонной плоскости, составляющей угол α с горизонтом, сообщается начальная скорость v₀, направленная вдоль плоскости. Коэффициент трения тела о плоскость равен µ. При каких значениях угла α время движения тела до остановки будет наименьшим?

 

Задача 2.70

Тело массой m движется прямолинейно с ускорением а по горизонтальной плоскости под действием некоторой силы F, составляющей с горизонтом угол α. Определить величину этой силы, если коэффициент трения между телом и плоскостью равен µ.

 

Задача 2.71

Ящик массой m = 60 кг тянут равномерно по горизонтальному полу с помощью веревки, образующей угол α = 30⁰ с полом. Коэффициент трения между ящиком и полом равен µ = 0,4. Определить силу натяжения веревки.

 

Задача 2.72

К нити подвешен груз массой m = 1 кг. Найти натяжение нити, если нить с грузом: 1) поднимать с ускорением а = 5 м/с²; 2) опускать с тем же ускорением а = 5 м/с².

 

Задача 2.73

Масса лифта с пассажирами равна 800 кг. Найти, с каким ускорением и в каком направлении движется лифт, если известно, что натяжение троса, поддерживающего лифт, равно: 1) 11760 Н: 2) 5880 Н.

 

Задача 2.74

К нити подвешена гиря. Если поднимать эту гирю с ускорением а₁ = 2 м/с², то натяжение Т нити будет вдвое меньше того натяжения, при котором нить разрывается. С каким ускорением а₂ надо поднимать эту гирю, чтобы нить разорвалась?

 

Задача 2.75

Автомобиль массой 1200 кг останавливается при торможении за 5 с, пройдя при этом, равнозамедленно 25 м. Найти начальную скорость автомобиля и силу торможения.

 

Задача 2.76

Вагон массой 20 т движется с начальной скоростью 54 км/ч. Определить среднюю силу, действующую на вагон, если известно, что вагон останавливается в течение: 1) 1 мин 40 с; 2) 10 с; 3) 1 с.

 

Задача 2.77

Какую силу надо приложить к вагону, стоящему на рельсах, чтобы вагон стал двигаться равноускоренно и за время t = 30 с прошел путь s = 11 м? Масса вагона m = 16 т. Во время движения на вагон действует сила трения, равная 0,05 силы тяжести вагона.

 

Задача 2.78

Вагон массой 20 т движется с постоянным отрицательным ускорением 0,3 м/с². Начальная скорость вагона равна 54 км/ч. 1) Какая сила торможения действует на вагон? 2) Через сколько времени вагон остановится? 3) Какое расстояние пройдет вагон до остановки?

 

Задача 2.79

Тело массой 0,5 кг движется прямолинейно, причем зависимость пройденного телом пути S от времени t дается уравнением S = А – Bt + Ct² - Dt³, где С = 5 м/с² и D = 1 м/с³. Найти силу, действующую на тело в конце первой секунды движения.

 

Задача 2.80

Под действием постоянной силы F = 9,8 Н тело движется прямолинейно так, что зависимость пройденного телом пути S от времени t дается уравнением S = А -Bt + Ct². Найти массу тела, если постоянная C = 1 м/с².

 

Задача 2.81

Трамвай, трогаясь с места, движется с постоянным ускорением а = 0,5 м/с². Через t = 12 с после начала движения мотор трамвая выключается, и трамвай движется до остановки равнозамедленно. На всем пути движения трамвая коэффициент трения равен µ = 0,01. Найти: 1) наибольшую скорость движения трамвая; 2) общую продолжительность движения; З) отрицательное ускорение трамвая при равнозамедленном движении; 4) общее расстояние, пройденное трамваем.

 

Задача 2.82

На автомобиль массой 1 т во время движения действует сила трения, равная его силы тяжести. Чему должна быть равна сила тяги, развиваемая мотором автомобиля, чтобы автомобиль двигался: 1) равномерно; 2) с ускорением 2 м/с²?

 

Задача 2.83

Железнодорожный вагон тормозится, и его скорость равномерно изменяется за время ∆t = 3,3 с от v₁ = 47,5 км/ч до v₂ = 30 км/ч. При каком предельном значении коэффициента трения между чемоданом и полкой чемодан при торможении начинает скользить по полке?

 

Задача 2.84

Канат лежит на столе так, что часть его свешивается со стола, и начинает скользить тогда, когда длина свешивающейся части составляет 25% всей его длины. Чему равен коэффициент трения каната о стол?

 

Задача 2.85

На автомобиль массой 1т во время движения действует сила трения равная 0,1 его силы тяжести. Найти силу тяги, развиваемую мотором автомобиля, если автомобиль движется с постоянной скоростью: 1) в гору с уклоном 1 м на каждые 25 м пути; 2) под гору с тем же уклоном.

 

Задача 2.86

Найти силу тяги, развиваемую мотором автомобиля, движущегося в гору с ускорением 1 м/с². Уклон горы равен 1 м на каждые 25 м пути. Масса автомобиля 1 т. Коэффициент трения равен 0,1.

 

Задача 2.87

Тело лежит на наклонной плоскости, составляющей с горизонтом угол 4⁰. 1) При каком предельном значении коэффициента трения тело начнет скользить по наклонной плоскости? 2) С каким ускорением будет скользить тело по плоскости, если коэффициент трения равен 0.03. 3) Сколько времени потребуется для прохождения при этих условиях 100 м пути? 4) Какую скорость тело будет иметь в конце этих 100 м?

 

Задача 2.88

Тело скользит по наклонной плоскости, составляющей с горизонтом угол α = 45⁰. Пройдя расстояние s = 36,4 см, тело приобретает скорость v = 2 м/с. Чему равен коэффициент трения тела о плоскость?

 

Задача 2.89

Тело скользит по наклонной плоскости, составляющей угол 45⁰ с горизонтом. Зависимость пройденного телом расстояния S от времени t дается уравнением S = Ct², где С = 1,73 м/с². Найти коэффициент трения тела о плоскость.

 

Задача 2.90

Тело скользит сначала по наклонной плоскости, составляющей угол α = 8⁰ с горизонтом, а затем по горизонтальной поверхности. Найти, чему равен коэффициент трения, если известно, что тело проходит по горизонтали такое же расстояние, как и по наклонной плоскости.

 

Задача 2.91

Тело массой m = 2 кг движется прямолинейно по закону S = А - Bt + Ct² - Dt³ (С = 2 м/с², D = 0,4 м/с³). Определить силу, действующую на тело в конце первой секунды движения.

 

Задача 2.92

Тело массой m движется так, что зависимость пройденного пути от времени описывается уравнением s = A*cos ωt, где А и ω - постоянные. Записать зависимость изменения силы от времени.

 

Задача 2.93

К нити подвешен груз массой m = 500 г. Определить силу натяжения нити, если нить с грузом: 1) поднимать с ускорением 2 м/с²; 2) опускать с ускорением 2 м/с².

 

Задача 2.94

Рис. 2.8 – Тело, лежащее на наклонной плоскости

На тело (см. рис.) массой m = 10 кг, лежащее на наклонной плоскости (угол α = 20⁰), действует горизонтально направленная сила F = 8 Н. Пренебрегая трением, определить: 1) ускорение тела; 2) силу, с которой тело давит на плоскость.

 

Задача 2.95

Тело массой m = 2 кг падает вертикально с ускорением а = 5 м/с². Определить силу сопротивления при движении этого тела.

 

Задача 2.96

С вершины клина, длина которого l = 2 м и высота h = 1 м, начинает скользить небольшое тело. Коэффициент трения между клином и телом µ = 0,15. Определить: 1) ускорение, с которым движется тело; 2) время прохождения тела вдоль клина; 3) скорость тела у основания клина.

 

Задача 2.97

По наклонной плоскости с углом α наклона к горизонту, равным 30⁰, скользит тело. Определить скорость тела в конце второй секунды от начала скольжения, если коэффициент трения µ = 0,15.

 

Задача 2.98

Рис. 2.9 - Вагон спускается по канатной железной дороге

Вагон массой m = 1 т спускается по канатной железной дороге с уклоном α = 15⁰ к горизонту (см. рис.). Принимая коэффициент трения µ = 0,05, определить силу натяжения каната при торможении вагона в конце спуска, если скорость вагона перед торможением v₀ = 2,5 м/с, а время торможения t = 6 с.

 

Задача 2.99

Наклонная плоскость, образующая угол α = 25⁰ с плоскостью горизонта, имеет длину l = 2 м. Тело, двигаясь равноускоренно, соскользнуло с этой плоскости за время t = 2 с. Определить коэффициент трения µ тела о плоскость.

 

Задача 2.100

Материальная точка массой m = 2 кг движется под действием некоторой силы F согласно уравнению х = А + Bt + Ct² + Dt², где С = 1 м/с², D = -0,2 м/с³. Найти значения этой силы в моменты времени t₁ = 2 с и t₂ = 5 с. В какой момент времени сила равна нулю?

 

Задача 2.101

Снаряд массой m = 10 кг выпущен из зенитного орудия вертикально вверх со скоростью v₀ = 800 м/с. Считая силу сопротивления воздуха пропорциональной скорости, определить время t подъема снаряда до высшей точки. Коэффициент сопротивления k = 0,25 кг/с.

 

Задача 2.102

С вертолета, неподвижно висящего на некоторой высоте над поверхностью Земли, сброшен груз массой m = 100 кг. Считая, что сила сопротивления воздуха изменяется пропорционально скорости, определить через какой промежуток времени ∆t ускорение а груза будет равно половине ускорения свободного падения. Коэффициент сопротивления k = 10 кг/с.

 

Задача 2.103

Моторная лодка массой m = 400 кг начинает двигаться по озеру. Сила тяги F мотора равна 0,2 кН. Считая силу сопротивления F_с пропорциональной скорости, определить скорость v лодки через ∆t = 20 с после начала ее движения. Коэффициент сопротивления k = 20 кг/с.

 

Задача 2.104

Катер массой m = 2 т трогается с места и в течение времени t = 10 с развивает при движении по спокойной воде скорость v = 4 м/с. Определить силу тяги F мотора, считая ее постоянной. Принять силу сопротивления F_с движению пропорциональной скорости; принять коэффициент сопротивления k = 100 кг/с.

 

Задача 2.105

Начальная скорость v₀ пули равна 800 м/с. При движении в воздухе за время t = 0,8 с ее скорость уменьшилась до v = 200 м/с. Масса m пули равна 10 г. Считая силу сопротивления воздуха пропорциональной квадрату скорости, определить коэффициент сопротивления k. Действием силы тяжести пренебречь.

 

Задача 2.106

Парашютист, масса которого m = 80 кг, совершает затяжной прыжок. Считая, что сила сопротивления воздуха пропорциональна скорости, определить, через какой промежуток времени ∆t скорость движения парашютиста будет равна 0,9 от скорости установившегося движения. Коэффициент сопротивления k = 10 кг/с. Начальная скорость парашютиста равна нулю.

 

Задача 2.107

Рис. 2.10 - Небольшое тело на горизонтальной поверхности

Небольшое тело массой m, находящееся на горизонтальной поверхности, движется прямолинейно под действием силы, равной по величине F (см. рис.). Коэффициент трения между телом и поверхностью равен µ. Под каким углом α к горизонту направлена сила F, если тело движется равномерно?

 

Задача 2.108

Брусок массой m тянут за нить так, как показано на рисунке к задаче 2,107. При этом он движется с постоянной скоростью по горизонтальной плоскости с коэффициентом трения µ. Найти угол α, при котором натяжение нити будет наименьшим. Чему оно равно?

 

Задача 2.109

По деревянным сходням, образующим угол α с горизонтом, втаскивают за веревку ящик. Коэффициент трения ящика о сходни равен µ. Под каким углом γ к горизонту следует тянуть веревку, чтобы с минимальным усилием втащить ящик?

 

Задача 2.110

Космический корабль массой m = 10⁶ кг начинает подниматься вертикально вверх. Сила тяги его двигателей F = 2,94*10⁷ Н. Определить ускорение корабля и вес тела, находящегося в нем, если вес этого тела на Земле P₀ = 600 H.

 

Задача 2.111

Цилиндрическое ведро с водой поднимают равноускоренно и за время t его скорость изменяется от v₀ до v. Зная, что масса воды равна m, а площадь основания ведра S, найти давление воды на дно.

 

Задача 2.112

Цилиндрический бак объемом V и площадью сечения S наполнен водой и установлен в лифте. Определить ускорение лифта, если давление воды на дно бака равно р. Плотность воды ρ.

 

Задача 2.113

Тележка весом Р = 196 Н может катиться без трения горизонтально. На тележке лежит тело массой m = 2 кг. Коэффициент трения между телом и тележкой µ = 0,25. К телу приложили горизонтальную силу F = 29,6 Н. Определить ускорения тележки и тела.

 

Задача 2.114

На столе лежит доска массой М = 2 кг, на которой находится брусок массой m = 1 кг, Коэффициенты трения между поверхностями бруска доски µ₁ = 0,4, доски и стола µ₂ = 0,1. С какими ускорениями будут двигаться брусок и доска, если к бруску приложена горизонтальная сила 1) F = 3 H; 2) F = 10 H.

 

Задача 2.115

На доске массой М лежит груз массой m. Какую силу нужно приложить к доске в горизонтальном направлении, чтобы выдернуть ее из-под груза? Коэффициент трения между грузом и доской µ₁, между доской и опорой µ₂.

 

Задача 2.116

С каким ускорением должна двигаться вверх лента транспортера, чтобы груз, находящийся на нем, по отношению к транспортеру был неподвижен? Угол наклона транспортера α. Коэффициент трения между грузом и поверхностью ленты µ > tg α.

 

Задача 2.117

Доска массой М, наклоненная под углом α к горизонту, лежит на двух опорах А и В, по которым она может скользить без трения вниз под действием силы тяжести. С каким ускорением и куда должен двигаться по этой доске человек массой m, чтобы доска не скользила?

 

Задача 2.118

Рис. 2.11 – Доска на наклонной плоскости

На наклонной плоскости с углом при основании α = 30⁰ лежит доска массой m₁ = 2 кг, а на доске брусок массой m₂ = 1 кг (см. рис.). Коэффициент доски о плоскость равен µ₁ = 0,2, бруска о доску µ₂ = 0,15. С какими ускорениями движется брусок и доска. предоставленные самим себе.

 

Задача 2.119

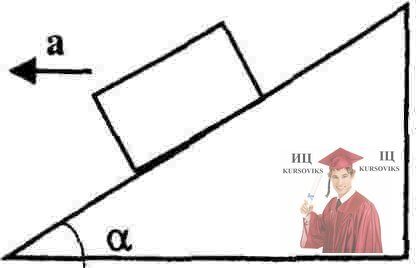
Рис. 2.12 - Наклонная плоскость с углом наклона α

Наклонная плоскость с углом наклона α движется с ускорением в сторону, показанную на рисунке. Начиная с какого значения ускорения а, тело, лежащее на наклонной плоскости, начнет подниматься? Коэффициент трения между телом и наклонной плоскостью равен µ < ctg α.

 

Задача 2.120

Рис. 2.13 – Призма на горизонтальной поверхности

На горизонтальной поверхности находится призма массой m₁ и углом при основании α, а на ней брусок массой m₂ (см. рис.). Пренебрегая трением, найти ускорение призмы. Задачу решить в системе отсчета, связанной с неподвижной горизонтальной плоскостью.

 

Задача 2.121

Материальная точка движется прямолинейно по закону , где α, β, γ - размерные коэффициенты, t — время, х - пройденный путь. Найти момент времени t, когда действующая на него сила станет равной нулю. Чему равна скорость точки в этот момент времени?

 

Задача 2.122

Материальная точка массой m = 1 г движется вдоль оси ОХ по закону х = 2t² - 4t³ [м], где t - время в секундах. Найти направление движения точки, величину и направление действующей на точку силы в моменты времени: а) t = 0,25 с; б) t = 0,5 с.

 

Задача 2.123

Задана зависимость от времени пути, пройденного автомобилем. S = 3t + 2t² + t³ [м]. Определить силу тяги автомобиля в момент времени t = 5 с после начала движения, если его масса М = 1 т.

 

Задача 2.124

Материальная точка массой m = 1 г движется вдоль оси ОХ. Пройденный путь в зависимости от времени описывается формулой х = β * 2^αt, где β = 1 м, α = 0,1 с^-1. Чему равна сила, действующая на точку в момент времени t = 10 с?

 

Задача 2.125

Скорость тела массой m, движущегося вдоль оси ОХ, меняется по закону v = v₀ - αx [м/с], где α - размерная постоянная. Как зависит сила, действующая на тело, от скорости v?

 

Задача 2.126

Скорость тела изменяется со временем по закону v = βt * e^-αt, где β = 1 м/с², α = 0,1 с^-1. Определить момент времени, когда скорость достигает максимального значения. Чему равна сила, действующая на тело в этот момент?

 

Задача 2.127

На скользкой дороге коэффициент трения между колесами велосипеда и дорогой µ = 0,1. При этом наибольшая скорость велосипеда v = 10 м/с. Сила сопротивления воздуха, действующая на велосипедиста, пропорциональна квадрату скорости велосипеда, т. е. F_с = α * v². Определить величину коэффициента пропорциональности α. Масса велосипеда вместе с велосипедистом М = 100 кг.

 

Задача 2.128

Небольшое тело массой m движется из состояния покоя сначала по гладкой горизонтальной плоскости под действием силы, изменяющейся со временем по закону: F = αt, где α - постоянная величина. В некоторый момент времени t₀ сила F исчезает, а тело продолжает движение уже по шероховатой горизонтальной поверхности с коэффициентом трения µ. Найти время движения тела по шероховатой поверхности.

 

Задача 2.129

На тележке массой М = 20 кг, которая может свободно перемещаться вдоль горизонтальных рельсов. лежит 6pуcoк массой m = 5 кг. Коэффициент трения между бруском и тележкой µ = 0,2. Брусок тянут с силой F, направленной параллельно рельсам. Найти ускорения бруска и тележки, если сила изменяется по закон F = αt, где α = 4 Н/c.

 

Задача 2.130

Брусок массой m₂ = 5 кг может свободно скользить по горизонтальной поверхности без трения. На нем находится другой брусок массой m₁ = 1 кг. Коэффициент трения соприкасающихся поверхностей брусков µ = 0,3. Определить максимальное значение силы F_max приложенной к нижнему бруску, при которой начнется соскальзывание верхнего бруска.

 

Задача 2.131

На горизонтальной поверхности находится брусок массой m₁ = 2 кг. Коэффициент трения µ₁ бруска о поверхность равен 0,2. На бруске находится другой брусок массой m₂ = 8 кг. Коэффициент трения µ₂ верхнего бруска о нижний равен 0,3. К верхнему бруску приложена сила F. Определить: 1) значение силы F₁, при котором начнется совместное скольжение брусков по поверхности; 2) значение силы F₂, при котором верхний брусок начнет проскальзывать относительно нижнего.

 

Задача 2.132

Рис. 2.14 – Обруч на плоской горизонтальной поверхности

На плоской горизонтальной поверхности находится обруч, масса которого ничтожно мала. К внутренней части обруча прикреплен груз малых размеров, как это показано на рисунке. Угол α = 30⁰. С каким ускорением а необходимо двигать плоскость в направлении, указанном на рисунке, чтобы обруч с грузом не изменил своего положения относительно плоскости? Скольжение обруча по плоскости отсутствует.

С уважением ИЦ "KURSOVIKS"!