Практическая работа №5 Структуры данных для представления сетей связи в виде графа

22 Практическая работа №5 Структуры данных для представления сетей связи в виде графа 20.03.2018 13:39

Практическая работа №5

с курса Цифровые системы коммутации

на тему: Структуры данных для представления сетей связи в виде графа

Широкий спектр задач, возникающих в процессе проектирования и эксплуатации телекоммуникационных сетей, решается с помощью методов теории графов с применением оптимальных комбинаторных алгоритмов. Математической моделью структуры сети служит граф с соответствующими характеристиками. Рассматривая методы решения задач на графах с позиции алгоритмической организации процесса обработки и последующей его программной реализации, очень важно использовать оптимальное представление данных. Во многих задачах, решаемых на графах, эффективность алгоритма зависит от выбора представления данных графа.

Сложность алгоритмов общепринято измерять по количеству арифметических операций и ячеек памяти, необходимых для его реализации.

Память (П) – количество ячеек памяти запоминающего устройства ЭВМ, требуемое для хранения данных при реализации алгоритма. Количество арифметических операций, выполненных алгоритмом, называется его трудоёмкостью (Т) или временной сложностью. Очевидно, что разные алгоритмы имеют разную трудоёмкость в зависимости от решаемой задачи и используемой структуры данных. Эффективными полиномиальными алгоритмами называются алгоритмы, Т и П которых ограничены сверху полиномиальной функцией от длины записи исходной информации. Если Т алгоритма нельзя оценить полиномом, то такой алгоритм называется экспоненциальным, и его считают неэффективным. Разница между полиномиальным и экспоненциальным алгоритмом возрастает с ростом размерности задачи.

В информатике способ представления данных определяется как структура данных. В частности, введены следующие структуры:

1) типы данных для представления целых и вещественных чисел, а также строковых значений;

2) n-мерные массивы для хранения множества однотипных данных;

3) структуры для объединения разнотипных данных в один логический элемент;

4) классы, как расширение структур за счет определения функций обработки данных класса.

За более подробными пояснениями следует обратиться к литературе [5].

В первой главе приводятся структуры данных для хранения графа и предлагаются варианты их использования для решения задач анализа и синтеза сетей связи.

1.1. Матричные представления графа

Представление сети связи в виде графа является адекватным и позволяет применить математический аппарат теории графов для задач моделирования сетей связи.

Обыкновенным графом G называется пара G=(V, E), где V – конечное непустое множество вершин, а E – конечное множество ребер. Каждому ребру соответствует пара вершин e=(v_i, v_j). Две вершины называются смежными, если между ними существует ребро. Ребро e инцидентно вершинам v_i, v_j, если e=(v_i, v_j).

Структура графа задает информацию о числе узлов сети (вершины графа — множество V), их взаимном расположении и взаимосвязи (ребра графа — множество Е). Каждому из элементов графа (вершины и ребра) могут быть поставлены в соответствие определенные характеристики элементов сети связи (к примеру, емкость узла, протяженность соединительной линии и ее емкость, и т.д.). Пример графического представления сети связи в виде графа G=(V, E) дан на рисунке 1(а). Однако, графическое представление удобно для отображения необходимой информации и восприятия ее человеком, но неприемлемо для алгоритмической обработки посредством ПЭВМ. Одним из возможных представлений графа в памяти ПЭВМ является матричное представление в виде двумерного массива целых чисел.

Если вершины и ребра графа пронумерованы целыми числами от 1…n и 1…m, где n-число вершин и m-число ребер, то доступ к элементам графа в структуре данных организуется по индексу, соответствующему номеру вершины или ребра.

Одним из самых распространенных представлений графа является матрица смежности. Матрица смежности имеет размер (n*n), число строк и столбцов которой соответствуют числу вершин графа, а элемент матрицы на пересечении i-ой строки и j-го столбца характеризует наличие ребра между этой парой вершин графа.

Для графа G=(V, E) на рисунке 1(а) матрица смежности B[n,n] = [b_ij] с числом вершин n=4 примет вид, приведенный на рисунке 1(б).

При этом b_{ij =} 1, если вершины i и j смежные, иначе b_{ij =} 0.

Матрица смежности обладает следующими свойствами:

- Для неориентированного графа матрица симметрична относительно главной диагонали.

- Сумма элементов в i-той строке или i-том столбце равна степени i-той вершины (количеству смежных вершин).

- Для хранения графа в виде двумерного массива требуется память П= |V|² =n ².

В случае, когда необходимо хранить данные о ребрах используют матрицу инцидентности. Число строк матрицы соответствует числу ребер графа, число столбцов равно числу вершин графа. Элемент матрицы задает инцидентность i-го ребра j-ой вершине. Так, для графа на рисунке 1(а) матрица инцидентности А[n,m] = [a_ij] приведена на рисунке 1(в), где n=4 – число вершин, m=9 – число ребер, элемент матрицы a_{ij =} 1 – если ребро i инцидентно вершине j, иначе a_{ij =} 0.

Свойства матрицы инцидентности:

- В каждой строке матрицы ровно две единицы.

- Сумма элементов j-го столбца равна степени j-той вершины.

- Для хранения графа требуется память объемом П= |V| |E| =n *m.

Рис. 1 – Структуры данных для представления графа

1.2. Списковые представления графа

В большинстве случаев при решении задач анализа и синтеза сетей матричные представления графа избыточны по памяти, а также трудоёмки для анализа элементов матрицы в процессе выполнения комбинаторных алгоритмов. Альтернативным представлением графа являются списковые структуры, которые описываются одномерными массивами данных.

Структура список ребер содержит два массива:

- массив номеров начальных вершин (введем для него обозначение IU[m]);

- массив номеров конечных вершин (OU[m]) по всем (m) ребрам графа.

Каждое k-е (к=1...m) ребро графа представляется элементами двух массивов IU[k] – номер начальной вершины k-го ребра, OU[k] – номер вершины-конца ребра. Если граф неориентированный, то в массивах неориентированное ребро представляется дважды – как e (v_i, v_j ) и e (v_j, v_i).

Граф G=(V, E) (рисунок 1(а)) представлен в виде списка ребер на рисунке 1(г). При этом ребрам графа присваивается номер (k) и по номеру ребра заносится значение номеров начальной и конечной вершин в соответствующие элементы массивов IU[k] и OU[k].

Для хранения графа требуется объем памяти П= 2* |E| =2 *m.

Более оптимальным отображением взаимосвязи вершин графа является структура смежности (список ребер с указателями). В этой структуре для каждой вершины задается список смежных с ней вершин.

Структура графа задается двумя массивами:

- массив указателей на списки смежности (UK[n+1]);

- массив списков смежных вершин (FO[m]).

Номер элемента i массива UK соответствует номеру вершины графа (i-тая вершина), для которой в массиве FO перечислены смежные вершины. Содержимое элемента UK[i] задает номер элемента массива FO, с которого для i-той вершины начинается список смежных с ней вершин. Массив FO содержит номера смежных вершин, которые сгруппированы и размещаются в элементах с номерами от UK[i] до UK[i+1]-1. Пример данного представления приведен на рисунке 1(д).

Для хранения графа требуется память объемом П= |V|+ |E| =n+m.

Если сеть представлена в виде взвешенного графа (рисунок 2(а)), то для представления информации о весах элементов графа необходимо ввести дополнительные структуры. Можно использовать при этом, как матричное, так и списковое представление.

В матричном представлении матрица весов ребер содержит равное число строк и столбцов по числу вершин графа, а элемент матрицы содержит вес соответствующего ребра. Однако, этот способ избыточен, тогда информацию о весах ребер можно сохранить аналогично списку ребер (рисунок 2(в)). Для представления весов вершин достаточно использовать одномерный массив по числу вершин графа, где в элементе хранится вес вершины с номером, равным номеру элемента массива (рисунок 2(б)).

Рис. 2 – Структуры данных для представления взвешенного графа

Если при описании ребер необходимо оптимизировать данные представления по объему памяти и времени обращения к элементу, то можно использовать представление в виде списков. В этом случае, сам граф должен быть задан в виде списка ребер с указателями. Тогда массив UK[n+1] используется для составления списков весов ребер (LF), которые упорядочиваются в соответствии со списками ребер в массиве FO[m]. Пример приведен на рисунке 2(г).

1.3. Анализ эффективности структур данных

Как было отмечено выше, эффективность алгоритмов на графах определяется двумя показателями: объемом памяти для хранения данных графа, и трудоемкостью алгоритма (количеством операций).

Рассмотрим описанные выше структуры с точки зрения эффективности алгоритмов на примере задачи "Нахождение степени вершин".

Для решения этой задачи необходимо определить структуру представления графа и, в соответствии с заданным представлением, для каждой вершины определить число смежных вершин. В зависимости от используемой структуры трудоемкость алгоритма изменяется следующим образом:

1. Если используем матрицу смежности, то требуется n просмотров элементов строки по каждой вершине графа (n). Т = n ² операций.

2. Для матрицы инциденций – n просмотров по m элементов. Т = n*m операций.

3. Список ребер – n просмотров по m элементов. Т = m*n операций.

4. Структура списка смежности – n раз выполнение операции вычитания (UK[i+1]-UK[i]). T = n.

1.4. Пример программы преобразования графа из структуры "список ребер" в структуру "список ребер с указателями"

Наиболее оптимальным представлением является структура списка смежности. Однако вручную построить данное представление достаточно трудоемко. Если же структура сети задается табличным представлением в базе данных в виде списка ребер (начало ребра– конец ребра), то в этом случае для трансформации "списка ребер" в "список ребер с указателями" следует написать универсальную процедуру, которая может преобразовывать списки рёбер любой размерности в соответствующие списки с указателями.

В качестве исходных данных возьмем следующие значения:

- n– число вершин графа сети;

- m – число ребер графа сети;

- исходные данные структуры графа сети заданы в виде списка ребер IU[m], OU[m], а также веса ребер заданы в массиве L[m].

Требуется сформировать структуру "список ребер с указателями" и сохранить в массивах UK[n+1], FO[m], LF[m].

Рассмотрим алгоритм преобразования.

Алгоритм:

1. Установить UK[0]=0 (для нулевой вершины список смежности начнется с нулевого элемента массива FO). Счетчик индекса для записи в массив FO установить равным нулю (s=0).

2. Задать цикл по вершинам i, в котором рассмотреть последовательно вершины с номерами от 0 до n. Счетчику цикла соответствует номеру вершины i (i=0…n).

2.1. Задать цикл по ребрам j для перемещения по элементам массивов IU[m], OU[m].

2.1.1. В массиве IU найти ребро, у которого IU[j]=i.

2.1.2. Записать найденную смежную с i вершину OU[j] в массив FO по индексу s. Для составления списков весов записать вес найденного ребра L[j] в массив LF по индексу s. Увеличить индекс обращения s=s+1.

2.1.3. Конец цикла по j.

2.2. Определить следующий указатель, т.е. указатель на список смежности (i+1)-ой вершины – UK[i+1]=s;

3. Конец цикла i по вершинам.

Задача №1. Для заданной графовой модели сети связи составить матрицу смежности.

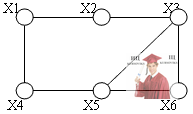
Задача №2. Для заданной графовой модели сети связи составить матрицу расстояний.

Задача №3. Для заданной о графовой модели сети связи составить матрицу инциденций.

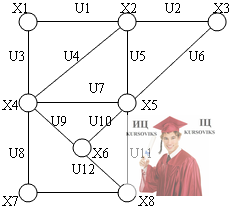
С уважением ИЦ "KURSOVIKS"!