Практическая работа №4 Связность графов. Множества сочленения и разделяющие множества

21 Практическая работа №4 Связность графов. Множества сочленения и разделяющие множества 20.03.2018 13:36

Практическая работа №4

с курса Цифровые системы коммутации

на тему: Связность графов. Множества сочленения и разделяющие множества

В теории графов, понятие связности графа является ключевым при решении многих прикладных задач.

Определение связного и несвязного графа.

Граф G(V,E) называется связным, если для любой пары различных вершин этого графа существует цепь, соединяющая эти вершины. Если для графа G(V,E) можно указать пару различных вершин, которые не соединяются цепью, то граф называется несвязным.

Нетрудно показать, что из существования цепи соединяющей две вершины графа, следует существование простой цепи, соединяющей эти вершины, поэтому граф является связным, если любую пару его вершин соединяет по крайней мере одна простая цепь.

Пример связного и несвязного графов.

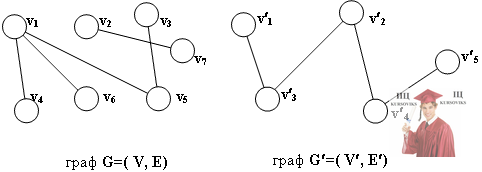
На рисунке выше, приведены примеры связного графа G' и несвязного графа G. Несложно видеть, что ни одна вершина из {v1, v3, v5, v6, v4} не может быть соединена цепью с вершинами v1 и v7, что показывает несвязность графа G. Напротив, любая пара вершин графа G' может соединяться простой цепью.

Сформулируем и докажем простой критерий несвязности произвольного графа.

Теорема 1.2. Граф G(V, E) является несвязным тогда и только тогда, когда множество его вершин V можно разбить на два не пустых подмножества V1 и V2 так, чтобы любое ребро графа соединяло вершины из одного подмножества.

Доказательство. Пусть G(V,E) - несвязный граф. Зафиксируем произвольную вершину А и обоз­начим через V1 множество, состоящее из вершины А и всех тех вершин из V, которые соединены цепями с вершиной А. Множество V1 не пусто, так как содержит, по крайней мере, вершину А, и не совпадает со множеством V (в противном случае граф G(V,Е) - связный, так как между его любыми двумя различными вершинами существует цепь, проходящая через А). Рассмотрим дополнение V2=V\V1. Множество V2 не пусто. Ясно, что никакое ребро графа G(V,E) не соединяет ни одну вершину из V1 ни с одной вершиной из V2. Поэтому построенные множества V1 и V2 образуют искомое разбиение множества V.

Обратно, пусть существует разбиение V = V1 V2, удовлетворяющее условию теоремы. Докажем, что G(V,E) -несвязный граф. Рассмотрим произвольную пару вершин из разных подмножеств A V1, B V2 , и докажем, что не существует цепи, соединяющей эти вершины. Действительно, если такая цепь существует, то она включает ребро, граничные точки которого принадлежат разным подмножествам, что противоречит условию теоремы.

Компоненты связности

Введем на множестве вершин графа G(V,E) бинарное отношение «связности» по следующему правилу. Положим что вершины u и v графа связны (и записывать u«v) тогда и только тогда, когда либо u=v, либо существует цепь, соединяющая вершины u и v.

Легко видеть, что отношение связности является

рефлексивным (v«v);

симметричным (u«v v«u);

и транзитивным (u«v, v«w u«w).

Следовательно, отношение ««» является отношением эквивалентности.

Компонентой связности графа G(V, E) называется каждый класс эквивалентности вершин, по отношению ««», вместе с ребрами из E, инцидентными этим вершинам.

Пример компонент связности графа.

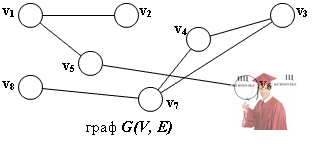
Рассмотрим пример двусвязного графа G(V, E). Всего имеется два множества связных между собой вершин V1 = {v1, v2, v5, v6} и V2 = {v3, v4, v7, v8}. По определению эквивалентности "", каждое из множеств вершин V1 и V2, вместе с инцидентными с ними ребрами, представляют два класса эквивалентности по отношению "", то есть являются компонентами связности.

Свойства компонент связности

1. Каждая вершина графа входит лишь в одну компоненту связности.

2. Любой конечный граф имеет конечное число компонент связности.

3. Граф, состоящий из единственной компоненты связности, является связным.

4. Каждая компонента связности графа является его подграфом.

Доказательство. Свойства 1-3 следуют прямо из определений. Докажем свойство 4. Пусть G1(V1,E1) - некоторая компонента связности графа G(V, E). Рассмотрим множество вершин V2=V-V1, не входящих в компоненту G1(V1,E1). Для каждой вершины из V2 применим операцию разборки вида 2, т.е. удалим эту вершину вместе со всеми инцидентными ей ребрами. Тогда, очевидно, получим подграф графа G(V, E), совпадающий с компонентой связности G1(V1,E1).

Из теоремы 1.1. вытекает следующая простая теорема.

Теорема 1.3. Если в конечном графе G ровно две вершины u и v имеют нечетную степень, то они связаны.

Доказательство. По теореме 1.1. каждый конечный граф имеет четное число вершин нечетной сте­пени. Так как это условие выполняется и для той компоненты G, которой принадлежит u, то v должно принадлежать той же компоненте.

Следующая теорема дает верхнюю оценку числа ребер в обыкновенном графе G.

Теорема 1.4. Пусть обыкновенный граф G имеет n вершин и k связных компонент. Тогда максимальное число ребер в G равно. (*)

Доказательство. Пусть в графе G компонента Gi имеет ni вершин. Тогда максимальное число ребер в G равно.

Это число достигается тогда, когда каждый из графов Gi полный и имеет ni вершин. Допустим, что среди графов G, найдутся хотя бы два, которые имеют более одной вершины, например, . Построим вместо G другой граф с тем же числом вершин и компонент, заменяя G1 и G2 полными графами и соответственно с и вершинами. Легко видеть, что это увеличивает число ребер. Таким образом, максимальное число ребер должен иметь граф, состоящий из k-1 изо­лированных вершин и одного полного графа с п-k+1 вершинами. Это число ребер описывается формулой (*).

В случае k=2 получаем следующее полезное следствие из теоремы 1.4.:

Следствие. Граф с n вершинами и с числом ребер большим чем связен.

Граф называется k-связным, если его любая пара различных вершин u и v соединяется по меньшей мере k простыми цепями, не имеющими общих вершин, кроме u и v.

Например связный граф является по крайней мере 1-связным графом. Вообще если граф является k-связным, то он является также и l-связным для любых l<k.

Числом связности обыкновенного графа G называется максимальное значение k, при котором граф G является k-связным. (Данное определение не включает случай графа с параллельными ребрами. Более общее определение будет дано ниже).

Если обыкновенный граф G содержит n вершин, то он является не более чем (n-1)-связным.

Теорема 1.5. В k-связном графе степень каждой вершины не меньше, чем k.

Доказательство. Предположим, что в графе существует некоторая вершина u степени deg(u)<k. Тогда вершину u невозможно соединить с любой другой вершиной k различными простыми цепями, не имеющими общих промежуточных вершин.

Следствия из теоремы 1.5.:

Подграф G1, полученный из k-связного графа G удалением одной вершины вместе со всеми инцидентными ей ребрами (операцией разборки вида 2) является не менее чем (k-1)-связным.

Суграф G1, полученный из k-связного графа G удалением одного ребра (операция разборки вида 1) является не менее чем (k-1)-связным.

Подграф G1, полученный из k-связного графа G удалением m вершин вместе со всеми инцидентными им ребрами (операция разборки вида 2 применяется m раз) является не менее чем (k-m)-связным.

Суграф G1, полученный из k-связного графа G удалением m ребер (операция разборки вида 1 применяется т раз) является не менее чем (k-m)-связным.

Следовательно, для того чтобы k-связный граф превратить в несвязный граф, необходимо удалить из него, по меньшей мере, либо k ребер, либо, по меньшей мере, k вершин. Если число k является максимально возможным, при котором граф G является k-связным, то существуют либо ровно k ребер, либо ровно k вершин, удаление которых превратит его в несвязный граф.

Таким образом, понятие k-связности графа тесно связано с минимальным количеством ребер (или вершин), удаление которых нарушает его связность.

Множеством сочленения графа G(V, E) называется любое непустое подмножество V1Ì V его вершин, удаление которых (операция разборки вида 2) превращает его в несвязный подграф. Если множество сочленения состоит из одной вершины, то она называется точкой сочленения.

Однако не для всякого графа существуют множества сочленения. К примеру полный граф не имеет множеств сочленения.

Из следствия 3 вытекает, что если обыкновенный граф является k-связным, то в нем нельзя выделить множество сочленения, состоящее менее чем из k вершин.

Сформулируем более общее (включающее графы с параллельными ребрами) определение числа связности. Пусть граф содержит n вершин.

Числом связности w(G) графа G называется либо наименьшее число элементов множества, являющегося множеством сочленения, либо число n-1, если граф не имеет множеств сочленения.

Заметим, что для обыкновенного k-связного графа G число k£w(G). Если k-связный граф G не обыкновенный, то число k может превышать число связности w(G).

Рассмотрим конечный связный граф G(V, E). Введем понятие разделяющего множества.

Разделяющим множеством графа называется непустое подмножество E1 его ребер (E1ÌЕ), удаление которых (операция разборки вида 1) превращает его в несвязный суграф. Если граф G имеет по крайней мере две вершины, то разделяющее множество всегда существует (например, E1 =E).

Пусть множество вершин V графа разделено на два подмножества W и W', так что WÇW= и W W' =V. Тогда множество ребер графа G, соединяющих вершины из W с вершинами из W', называется разрезом, разделяющим W и W'.

Очевидно, что любой разрез является разделяющим множеством. Обратное, вообще говоря, неверно.

Разделяющее множество называется простым разрезом, если оно является минимальным, т.е. не содержит собственного подмножества, разделяющего граф.

Любой простой разрез является разрезом, но не всякий разрез является простым.

Разделяющее множество, состоящее из единственного ребра, называется перешейком (или мостом).

Ясно, что любой перешеек есть простой разрез. Также легко заметить, что граничные точки любого перешейка всегда являются точками сочленения. Сделаем еще одно дельное замечание: перешейки и точки сочленения являются самыми узкими местами в графах транспортных сетей и наиболее сильно ограничивают их пропускную способность. Достаточно перекрыть всего один перешеек или всего одну точку сочленения, чтобы парализовать сообщение.

Задачи на связность

Задача №1. Задан граф G. Сколько компонент связности содержит граф G?

Задача №2. Задан граф G. Сколько компонент связности содержит граф G?

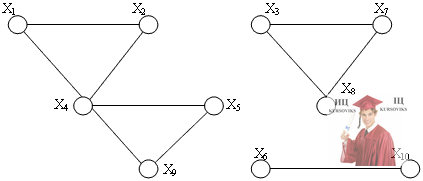
Задача №3. Какой из графов содержит 3 компоненты связности?

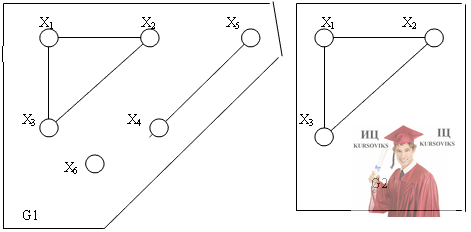
Задача №4. Компонентой связности называется:

а) Суграф исходного графа G, не содержащий циклов и имеющий столько же компонент связности, что и исходный граф;

б) Максимальный подграф графа G, в котором все вершины попарно достижимы;

в) Часть графа без циклов, связывающая заданное множество вершин.

С уважением ИЦ "KURSOVIKS"!