Практическая работа №3 Маршруты, цепи, циклы, пути

Практическая работа №3

с курса Цифровые системы коммутации

на тему: Маршруты, цепи, циклы, пути

Пусть задан некоторый граф G. Каждое ребро этого графа можно интерпретировать как связующее звено между двумя смежными вершинами. Если зафиксировать некоторую вершину графа и последовательно переходить по связующим ребрам из вершины в вершину, то по прошествию конечного числа таких переходов можно перейти в другую вершину или вернуться в исходную. В теории графов такие непрерывные последовательности, по которым можно переходить от одной вершины к другой, играют важное значение как при определениях различных понятий, так и при доказательствах теорем. Опишем наиболее важные непрерывные последовательности ребер графа.

Пусть задан конечный граф G(V, Е).

Маршрутом длины k называется конечная последовательность ребер графа такая, что конечные точки двух соседних ребер этой последовательности совпадают. Иначе говоря, существует последовательность (не обязательно различных) смежных вершин. Вершины и называются соответственно начальной и конечной вершиной маршрута или просто концевыми вершинами.

Пример маршрутов.

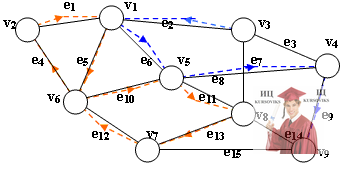
На рисунке изображен неориентированный граф G, на котором оранжевой стрелкой показан маршрут m = ( e1, e5, e10, e11, e13, e12, e4). Этому маршруту соответствует последовательность вершин n = ( v2, v1, v6, v5, v8, v7, v6, v2). В маршруте m начальная и концевая вершины v2 совпадают, следовательно, m - конечный замкнутый маршрут длины 7, все ребра которого различны, то есть m является цепью. В последовательности n смежных вершин, входящих в замкнутую цепь m, имеются повторяющиеся вершины, например v2 и v6. Следовательно, m - не простая замкнутая цепь, то есть цикл.

Рассмотрим маршрут отмеченный синей стрелкой m' = ( e2, e6, e8, e9), которому соответствует последовательность вершин n' = ( v3, v1, v5, v4, v9). Заметим, что маршрут m' открытый, цепь без повторяющихся вершин. Следовательно, маршрут m' - путь или простая цепь.

Маршрут называется замкнутым, если его начальная и конечная вершины совпадают, иначе маршрут называется открытым.

Маршрут называется цепью, если все его ребра различны.

Цепь называется замкнутой, если ее начальная и конечная вершины совпадают, иначе цепь называется открытой. Замкнутая цепь называется циклом.

Граф называется ациклическим, если в нем нет циклов.

Открытая цепь называется простой цепью или путем, если все вершины ее различны. Замкнутая простая цепь называется простым циклом.

Свойства путей и циклов.

Степень каждой неконцевой вершины пути равна 2, степень концевой вершины равна 1.

Каждая вершина цикла имеет четную степень.

Число вершин в пути на единицу больше, числа ребер. В цикле число вершин равно числу ребер.

Если в графе существует цепь, соединяющая две вершины, то в графе существует путь (простая цепь) соединяющая две эти вершины.

Во многих прикладных задачах, в особенности при моделировании сетей связи, важную роль играют циклы специального вида.

Задачи на маршруты, цепи, циклы в графах.

Задачи 1 уровня сложности.

Простой цикл, проходящий через все вершины графа, называется гамильтоновым циклом, а простая цепь, обладающая этим свойством - гамильтоновой цепью.

Связный неориентированный граф называется гамильтоновым графом, если все его вершины можно включить либо в простую цепь (гамильтонова цепь), либо в простой цикл (гамильтонов цикл).

Пример гамильтонова графа и гамильтонова цикла.

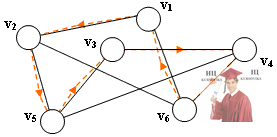
На неориентированном графе G. Оранжевой стрелкой отмечен простой цикл m. Ему соответствует последовательность вершин n = ( v1, v2, v5, v3, v4, v6, v1). Нетрудно видеть, что простой цикл m проходит через все вершины графа G, поэтому является гамильтоновым циклом. Чтобы получить пример гамильтоновой цепи в графе G, следует из маршрута m исключить одно любое ребро. Неориентированный граф G- гамильтонов.

Если все ребра графа можно включить в простой цикл, то такой уникурсальный граф называется эйлеровым циклом. Уникурсальный граф, не являющийся эйлеровым циклом, называется эйлеровой цепью.

Граф называется уникурсальным графом (или эйлеровым), если все его ребра можно включить либо в простой цикл, либо в простую цепь.

Пример уникурсального графа и эйлерова цикла.

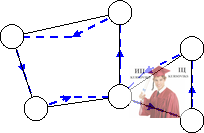
Рассмотрим пример неориентированного уникурсального графа G изображенного на рисунке. Синей стрелкой на графе G отмечен эйлеров цикл, проходящий через все ребра графа. Следовательно, графе G – уникурсальный или эйлеров цикл.

Задачи на маршруты и цепи в графах

Задача №1. Простой цепью называется:

а) Чередующаяся последовательность типа x1, u1, x2, u2,…xn, в которой любая пара инцидентна;

б) Цепь, в которой все ребра и вершины различны;

в) Маршрут, в котором все ребра различны;

г) Цепь, у которой начальная и конечная вершины совпадают.

Задача №2.Что называется маршрутом в графовых моделях?

а) последовательность вида U1 U2 U3 U4 …Un

б) последовательность вида Х1 U1 Х2 U2 X3 U3 …Хn Un

Задача №3. Простой цепью называется:

а) Чередующаяся последовательность типа X1 U1 X2 U2…Xn, в которой любая пара инцидентна;

б) Цепь, в которой все ребра и вершины различны;

в) Маршрут, в котором все ребра различны;

г) Цепь, у которой начальная и конечная вершины совпадают.

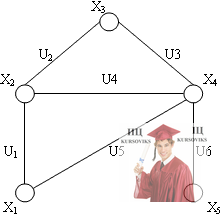
Задача №4. Написать все возможные маршруты от вершины X2 до вершины X5.

Задача №5. В какой из представленных графовых моделей имеется один цикл? (G1, G2, G1 и G2, ни в одном).

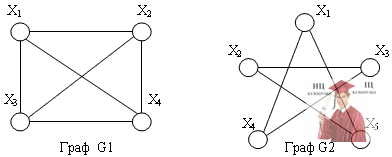
Задача №6. Напишите маршрут из вершины X1 до вершины X5 с минимальным количеством ребер.

С уважением ИЦ "KURSOVIKS"!