Практическая работа №2 Классы конечных графов

19 Практическая работа №2 Классы конечных графов 20.03.2018 13:27

Практическая работа №2

с курса Цифровые системы коммутации

на тему: Классы конечных графов

Некоторые конечные графы имеют в литературе специальные названия. Приведем наиболее употребляемые термины.

Классы графов определяются по типу ребер.

Обыкновенным или простым графом называется конечный граф без петель и параллельных ребер.

Мультиграф – граф, который содержит мультиребра.

Псевдограф – граф, содержащий петли.

Взвешенный граф – если вершинам или ребрам приписаны веса (числовые характеристики). Вес вершины обозначается w(v), вес ребра - w(e).

Ориентированный граф – содержит только ориентированные ребра.

Множество Е={e_k | e_k=(v_i;v_j)} в этом случае состоит из упорядоченных(!) пар элементов множества V, при этом первая вершина называется началом ребра, а вторая концом ребра.

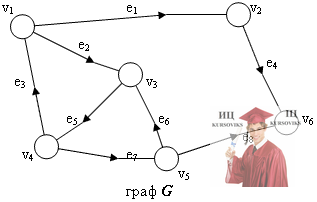
Пример ориентированного графа.

На рисунке изображен граф G=(V,E), где V={v1, v2, v3, v4, v5, v6 } множество вершин, а E={e1, e2, e3, e4, e5, e6, e7, e8} множество направленных ребер. В этом примере E={(v1, v2), (v1,v3), (v1, v4), (v2, v6), (v3, v4), (v5, v3), (v4, v7), (v5, v6)}, причем порядок вершин существенен.

Неориентированный граф – содержит только неориентированные ребра.

Смешанный граф – содержит и ориентированные и неориентированные ребра.

Типы графов определяются по количеству ребер.

Полный граф – обыкновенный граф, у которого каждая пара вершин соединена ребром, полный граф обозначается Kp. Заметим что в полном графе число ребер m=n× (n-1)/2, где n – число вершин.

Пример полного графа.

Ниже приведены примеры полных графов K5 ,K4 ,K3 с числом вершин 5, 4 и 3 соответственно. Несложно проверить, что число ребер в этих графах можно вычислить по формуле число ребер=n× (n-1)/2, где n – число вершин.

K5 K4 K3

Пустой граф – не содержит ни одного ребра (m=0)

Планарный граф – если граф можно разложить на плоскости без пересечения ребер (m£3n-6) , плоский граф – если граф уже изображен на плоскости без пересечения ребер.

Пример планарного и плоского графа.

На рисунке слева изображен планарный граф G1, который можно расположить на плоскости без пересечения ребер. На рисунке справа изображен тот же плоский граф G1.

Дерево – граф, имеющий n вершин и n-1 ребер. Вообще ниже будут предложены несколько эквивалентных определений дерева, так что можно пользоваться любым из них.

Регулярный граф – граф, у которого степени всех вершин равны.

Степенью регулярного графа называется степень его вершин. Степень регулярного графа G обозначается через deg G.

Пример регулярного графа. Степень регулярного графа.

На рисунке 4 изображены три регулярных графа K5 ,K4 ,K3 . У каждого графа степени его вершин равны между собой, при этом deg K5 = 4, deg K4 = 3, deg K3 = 2. Заметим в общем, что любой полный граф является регулярным графом, но не наоборот. Например, граф изображенный ниже, регулярный, но не полный.

Примерами регулярных графов являются полные графы и графы платоновых тел.

Из леммы о рукопожатиях вытекает, что не существует регулярного графа, порядок и степень которого нечетны.

Двудольный граф – граф, множество вершин которого можно разбить на два подмножества V1 и V2 так, что каждое ребро имеет один конец в V1, а другой в V2. Двудольный граф G c такими подмножествами V1 и V2 обозначается как G(V1, V2, E).

Двудольный граф обыкновенный, если он не содержит параллельных ребер. Обыкновенный двудольный граф полный, если любая пара вершин из разных подмножеств соединена ребром (см. рис. 1). Полный двудольный граф содержит |Е|=|V2|×|V2| ребер.

Примеры двудольных графов

На рисунке изображены двудольный граф G=(V1, V2, E), обыкновенный двудольный граф G'=(V'1,V'2, E'), и полный двудольный граф G''=(V''1,V''2, E'').

k-дольным графом (при k > 2) называется мультиграф, вершины которого можно разделить на k непересекающихся подмножеств так, чтобы ребра не соединяли вершины из одного подмножества.

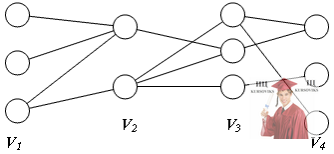
Пример k-дольного графа.

На рисунке изображен пример 4-дольного графа G(V1, V2, V3, V4, E). В нем присутствуют четыре непересекающихся подмножеств вершин V1, V2, V3 и V4 так, что каждое ребро имеет концы в разных подмножествах вершин.

Любой мультиграф с n вершинами можно рассматривать как n-дольный граф. Каждая его «доля» состоит всего из одной вершины. В частности, полный граф с n вершинами является n-дольным графом и не является k-дольным графом для k < п.

Условие существования регулярного графа данного порядка и степени.

Если данные натуральные числа n и d, среди которых есть четное, удовлетворяют неравенствам 0£ d £ n-1, то существует регулярный граф порядка n и степени d.

Свойство регулярного двудольного графа.

Если G=(V1, V2, E) - непустой регулярный двудольный граф, то |V1|=|V2|.

Задачи на типы графов

Задача №1. Какой граф называется полным?

а) граф в котором любая пара вершин смежна.

б) граф в котором пара вершин смежна.

в) граф в котором вершины не смежны.

г) граф в котором любая пара ребер смажна.

Задача №2. Определите какой граф называется тривиальным:

а) состоящий из двух вершин.

б) состоящий из одной вершины.

в) граф без ребер.

Задача №3. Граф называется планарным если:

а) при расположении на плоскости ребра пересекаются.

б) при расположении на плоскости ребра не пересекаются.

Задача №4. Граф называется пустым если:

а) пара вершин не смежна.

б) любая пара вершин не смежна.

в) любая пара вершин смежна.

Задача №5. Определите какая графовая модель G1 или G2 является ографом. (G1 или G2)

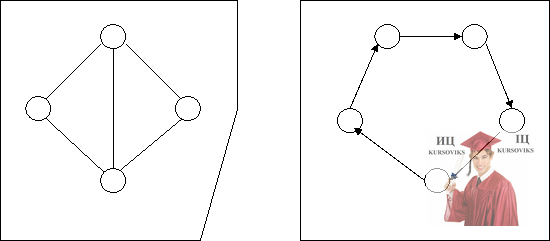
G1 G2

Задача №6. Представленная модель является ориентированным графом?

(да, нет)

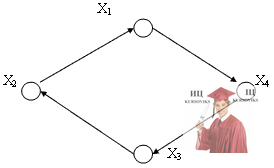
Задача №7. Какая модель является обыкновенным графом. (G1 или G2)

Задача №8. Определите какая графовая модель G1, G2 или G3 является полным графом.

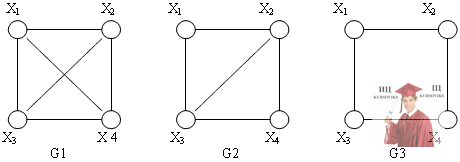
Задача №9. Является ли граф на рисунке графом K3? (да, нет)

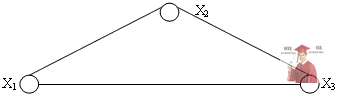
Задача №10. Граф обыкновенный, если он:

а) неориентированный граф без петель

б) ориентированный граф с петлями.

в) связный граф без петель.

г) неориентированный граф с петлями.

С уважением ИЦ "KURSOVIKS"!