18 Практическая работа №1 Основные понятия теории графов 20.03.2018 13:18

Практическая работа №1

с курса Цифровые системы коммутации

на тему: Основные понятия теории графов

Содержание

1. Начальные определения. 3

2. Операции над графами. Части графа. 6

3. Изоморфизм графов. 11

Задачи. 13

1. Начальные определения

Начало теории графов как математической дисциплины было положено Эйлером в его знаменитом рассуждении о Кёнигсбергских мостах. Однако эта статья 1736 года, была единственной в течении почти ста лет. Интерес к задачам теории графов возродился около середины уже позапрошлого столетия и был сосредоточен в областях электрических цепей, моделей кристаллов и структур молекул. Хотя, строго говоря, термин “граф” впервые появился в книге венгерского математика Д. Кенига только в 1936 г., но многочисленные прикладные задачи и головоломки (которые, кстати, поддавались формулировкам в терминах графов) привели к пониманию, что эти задачи содержат некоторое математическое ядро, важность которого выходит за рамки конкретного вопроса.

Предметом первых исследований в теории графов были конфигурации, состоящие из точек и соединяющих их линий. В этих рассмотрениях было несущественно, прямые это линии или криволинейные дуги, где они расположены, являются ли они длинными или короткими. Существенным являлось только то, что они соединяют две данные точки. Это привело к определению графа как абстрактного математического понятия.

Графом называется пара (V,E), где V - непустое множество элементов, называемых вершинами графа, а E - множество неупорядоченных пар элементов из V, называемых ребрами графа.

Если V={v1, v2,…vn}, то множество ребер E={e1,e2,…em} задается отображением EÍV´V. Элементы множества Е обозначаются как ек=(vi,vj). Множества вершин и ребер графа G обозначают V(G) и Е(G) соответственно. Число вершин и ребер в графе обозначаются через |V(G)| и |E(G)|. Если |V(G)|=n и |E(G)|=m, то говорят об (n,m)-графе.

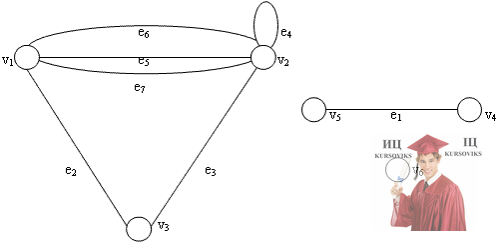
Рис. 1 - Граф G=(V,E), где V={v1, v2, v3, v4, v5, v6} множество вершин, а E={e1, e2, e3, e4, e5, e6, e7} множество ребер

Граф называется конечным, если множества V и Е содержат конечное число элементов.

Две вершины называются смежными, если между ними есть ребро.

Ребро называется инцидентным вершине, если вершина является его началом или концом.

Вершина, не смежная ни с одной другой вершиной, называется изолированной.

Ребро называется петлей, если оно инцидентно одной вершине.

При изображении графа петля представляется замкнутой дугой, начинающейся и заканчивающейся в одной вершине.

Если между парой вершин имеется более одного ребра, то такое ребро называется мультиребром. Ребра графа называются параллельными, если они инцидентны одним и тем же вершинам, т.е. если они соединяют одну и ту же пару вершин.

Степенью вершины называется число инцидентных ей ребер. Степень вершины v обозначается через deg v.

Если степень вершины равна 1, то она называется концевой или висячей вершиной. Вершина, степень которой больше или равна 2, называется промежуточной или проходной. Вершины графа называются четными или нечетными в зависимости от четности их степеней.

Теорема 1.1. В любом конечном графе G(V,E) количество нечетных вершин - четно.

Доказательство. Действительно, каждое ребро добавляет по единице к степеням своих граничных вершин, а каждая петля добавляет двойку к степени своей вершины. Поэтому сумма степеней всех вершин равна удвоенному числу ребер графа. Следовательно, сумма степеней всех вершин графа есть четное число. Поэтому в эту сумму может входить лишь четное количество нечетных слагаемых, т.е. количество нечетных вершин графа G есть четное число.

Следствие (“Лемма о рукопожатиях “). Сумма степеней всех вершин конечного графа равна удвоенному числу ребер:

å deg v=2|E(G)|.

vÎV(G)

2. Операции над графами. Части графа

Пусть задан некоторый конечный граф G(V, E). Существует ряд операций, называемых операциями разборки графа, позволяющих из исходного графа получать новые графы, множества вершин которых являются подмножествами множества V, а множества ребер - подмножествами множества E. При этих операциях должно сохраняться отношение инцидентности, имеющее место для исходного графа G при выполнении разумного требования о том, что множество вершин получившегося графа G1 должно включать все конечные точки множества его ребер.

Существует два основных вида операций разборки графа G:

1) удаление ребра между двумя вершинами графа G с сохранением конечных вершин;

2) удаление вершины графа G вместе со всеми ей инцидентными ребрами.

Частным случаем второй операции разборки является операция

2*) удаление изолированной вершины графа G.

Граф G1, полученный из графа G при помощи конечного числа операций разборки, называется частью графа G.

Пример.

Этот пример иллюстрирует применение операций 1) и 2) к графу G.

На рисунке 3 изображены три графа: G, G' и G''. Нетрудно заметить, что граф G' получается из графа G применением операции 1), а именно удалением ребер e1, e6.

Граф G'' получается из графа G применением операции 2), при этом удаляется вершина v3 и инцидентные ей ребра e3, e2.

Рис. 2 - Пример разбора графа G=(V,E)

Подграфом графа G называется такая его часть G1, которая получается из графа G при помощи конечного числа операций разборки вида 2, т.е. - при помощи удаления конечного числа вершин вместе со всеми примыкающими к ним ребрами. Другими словами, подграф G1 - это такая часть графа G, для которой E1 - все ребра из E, концы которых лежат в V1. Граф G по отношению к своему подграфу G1 называется надграфом.

Суграфом графа G называется такая его часть G1, которая получается из графа G при помощи конечного числа операций разборки вида 1, т.е. при помощи удаления конечного числа ребер (с сохранением вершин). Другими словами, суграф G1 - это такая часть графа G, для которой V1 = V. Иногда такую часть графа называют остовным подграфом (или фактором). Граф G по отношению к своему суграфу G1 называется сверхграфом.

Пример части графа, подграфа, надграфа.

Посмотрим на рисунок 2. Согласно определению понятия «части графа», графы G' и G'' являются частями графа G, поскольку получены применением операций разборки вида 1) и 2) соответственно.

Граф G'' получен из графа G при помощи операции разборки 2, поэтому G'' является подграфом графа G. Граф G, по отношению к графу G'', будет его надграфом.

Пример суграфа и сверхграфа.

На рисунке 2 граф G' получается из графа G применением операции разборки вида 1, поэтому G' является суграфом графа G. Граф G, по отношению к графу G', будет его сверхграфом. Заметим в общем, что число вершин суграфа и его сверхграфа одинаковое, по определению операции 1.

Также существует ряд дополнительных операций над графами, позволяющих получать из исходного графа G новый граф G1.

3) Добавление вершины в граф. Пусть v “новая вершина”. Тогда V(G1)=V(G)+v.

4) Добавление ребра в граф. Пусть u и v вершины графа G . Тогда можно определить граф E(G1)=E(G)+e, где е=(u,v).

5) Отождествление (или слияние) вершин в графе. Пусть u и v – две вершины графа G. Удалим их вместе с инцидентными им ребрами и добавим новую вершину w, соединив ее ребрами с каждой из вершин, смежных вершинам u и v в графе G. Говорят, что построенный граф G1 получается из графа G отождествлением вершин u и v.

Примеры дополнительных операций над графами.

Пример применения операции «слияние вершин в графе». В этом примере вершины u и v графа G отождествляются в вершину w. Получается граф G1 изображенный на рисунке.

Пример операции «стягивание ребра в графе». Граф G1 получается из графа G стягиванием ребра

6) Стягивание ребра в графе. Стягивание ребра е=(u,v) означает отождествление смежных вершин u и v. При этом вместо вершин u и v появляется новая вершина, смежная с каждой из вершин, смежных вершинам u и v.

Рис. 3 - Иллюстрация операции «слияние вершин в графе»

7) Объединение графов. Граф H называется объединением графов F и G, если V(H)=V(F)UV(G) и E(H)=E(F) U E(G). В этом случае пишут H=F U G.

Пример.

Пример операции «объединение графов». V(F)={v1,v2, u}, V(G)={v3, u} V(H)=V(F)UV(G)={v1,v2, v3, u} и E(H)=E(F) U E(G). Значит H=F U G.

Рис. 4 - Иллюстрация операции «объединение графов»

8) Дополнение графа. Дополнение Ġ произвольного графа G возможно определить следующим образом: V(Ġ)=V(G), и любые две несовпадающие вершины смежны в Ġ тогда и только тогда, когда они не смежны в G. Очевидно, что если операцию построения дополнительного графа применить два раза, то получим исходный граф.

Пример операции «дополнение графа». На рисунке изображено дополнение Ġ графа G, V(Ġ)=V(G), причем любые две несовпадающие вершины смежны в Ġ тогда и только тогда, когда они не смежны в G.

Рис. 5 - Иллюстрация операции «дополнение графа»

9) Получение реберного графа. Реберным графом L(G) графа G называется граф, вершинами которого являются ребра графа G, и две вершины графа L(G) смежны тогда и только тогда, когда смежны соответствующие им ребра графа G.

Пример операции «получение реберного графа». Вершинами графа L(G) являются ребра графа G, и две вершины графа L(G) смежны когда смежны соответствующие ребра графа G.

Рис. 6 - Иллюстрация операции «получение реберного графа»

10) другие операции.

3. Изоморфизм графов

Два графа G и G1 называются изоморфными, если между их однотипными элементами можно установить взаимно однозначные соответствия, сохраняющие отношение инциденции.

Пример. Пусть заданы два графа G и G1.

Рис. 7 - Изоморфизм

Определим взаимно однозначное соответствие I между элементами этих графов при помощи пары отображений I1: V®V1 и I2: E®E1, заданных по формулам:

I1(Ai)=Bi, I2(ai)=bi.

Легко видеть, что две вершины графа G соединены ребром тогда и только тогда, когда соответствующие вершины графа G1 соединены соответствующим ребром. Поэтому построенное взаимно однозначное соответствие I = (I1; I2) между элементами графов G и G1 сохраняет отношение инциденции. Следовательно, графы G и G1 изоморфны, то есть с точки зрения теории графов являются равными или одинаковыми.

Отображением изоморфизма (или просто изоморфизмом) G на G1 называется взаимно однозначное соответствие I = (I1;I2), состоящее из пары отображений I1 и I2 и обеспечивающее изоморфизм графов. Граф G изоморфен графу G1 тогда и только тогда, когда существует отображение изоморфизма G на G1, и обозначается G ~G1.

Рассмотрим отношение «~» на множестве всех графов. Просто показать, что оно является отношением эквивалентности, т.е. удовлетворяет следующим условиям:

1. G~G - рефлексивности;

2. G ~ G1 Þ G1 ~ G - симметричности;

3. G ~ G1, G1 ~ G2 Þ G ~ G2 - транзитивности.

Поэтому множество всех графов распадается на непересекающиеся классы изоморфных графов.

Задачи

1 ур. сложности.

Задача №1. Задан граф G в геометрическом представлении. Представить граф G в теоретико-множественном виде.

Задача №2. Задан граф G в геометрическом виде. Представить данный граф G в теоретико-множественном виде.

Задача №3. Граф G задан теоретико-множественным способом. Представить граф G геометрическим способом.

X1, X2, X3, X4 U1® X1, X2 U3 ® X1, X4

U1, U2, U3, U4 U2 ® X1, X3 U4 ® X3, X4

Посмотреть ответ.

Задача №4. Каким способом представлен граф G?

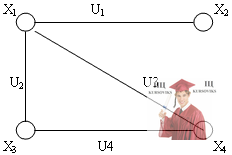
Задача №5. Задан граф G в геометрическом представлении. Представить данный граф G в теоретико-множественном виде.

2 ур. сложности.

Задача №1. Задан граф G в геометрическом представлении. Представить данный граф G в теоретико-множественном виде.

Задача №2. Задан граф G в геометрическом представлении . Представить данный граф G в теоретико-множественном виде .

Задача №3. Задан граф G в геометрическом представлении. Представить данный граф G в теоретико-множественном виде.

С уважением ИЦ "KURSOVIKS"!