Методические рекомендации к лабораторной работе №3 с курса Информационные системы и технологии, Финансовый анализ данных

12 Методические рекомендации к лабораторной работе №3 с курса Информационные системы и технологии, Финансовый анализ данных 01.03.2018 15:17

Цель работы: приобрести навыки принятия управленческих решений на основе финансово-экономических расчетов с использованием встроенных функций категорий «Финансовые» ТП MS Excel.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Несмотря на наличие специализированных банковских и аналитических систем, для проведения финансово-экономических расчетов ЭТ Excel, в свою очередь, предлагают пользователю значительное количество специальных функций, объединенных в категорию «Финансовые».Эти функции составляют основу любых финансово-экономических расчетов и могут использоваться при анализе финансового состояния предприятий, банков и любых других учреждений; в финансовом менеджменте: в оценке инвестиционных проектов; расчете доходов от ценных бумаг, в решении задач финансово-экономического прогнозирования.

Условно финансовые функции Excel можно разделить на три блока:

- анализ инвестиций (вложений),

- доходы от ценных бумаг (процентные ставки),

- вычисление амортизации.

Анализ инвестиций

Для инвестиционного анализа могут использоваться такие стандартные функции Excel, как ПС - текущий объем вклада, ЧПС - чистая приведенная стоимость, БС - будущее значение вклада, ПЛТ, ПРПЛТ, ОСПЛТ -периодические выплаты по займу, КПЕР - срок выплаты по займу и некоторые другие.

- Функция ПС (ставка; кпер; выплата; бс; тип) – рассчитывает приведенный к текущему моменту объем вклада на основе постоянных выплат (аргументы функции ПС см. табл. 4.1).

Таблица 4.1 - Аргументы функции ПС

Ставка	Процентная ставка за период
КПЕР	Общее число периодов выплат годовой ренты
ВЫПЛАТА	Выплата, производимая в каждый период; это значение не может меняться в течение всего периода выплат.
БС	Будущая стоимость, которую нужно достичь после последней выплаты.
ТИП	Число 0 или 1, обозначающее, когда должна производиться выплата: если в начале периода, тип равен 1, если в конце периода, тип опущен или равен 0.

- Функция ЧПС(ставка; значение1; значение2; …; значение2 9)

значение1; значение2; …; значение29 – это дисконтированные денежные поступления в течение прогнозируемого срока.

Таким образом, функция ЧПС отличается от функции ПС тем, что в функции ЧПС периодические выплаты могут быть различными; платежи (поступления) функции ПС допускаются как в начале, так и в конце периода, а в функции ЧПС все выплаты производятся равномерно в конце периода.

- Функция БС(ставка; кпер; выплата; пс; тип) – возвращает будущее значение вклада на основе периодических постоянных платежей и постоянной процентной ставки. Будущее значение является величиной, противоположной настоящему объему вклада.

- Функция ПЛТ(ставка; кпер; пс; бс; тип) – рассчитывает постоянные периодические выплаты при возврате займа в течение определенного периода.

- Функция ПРПЛТ(ставка; период; кпер; пс; бс; тип) – возвращает платежи по процентам за текущий период на основе постоянных периодических выплат и постоянной процентной ставки.

- Функция ОСПЛТ(ставка; период; кпер; пс; бс; тип) – рассчитывает величину основного платежа по займу на основе постоянных периодических выплат и постоянной процентной ставки.

Расчет амортизации

Для расчета амортизации (степени износа) имущества в течение определенного периода можно использовать такие функции как АМОРУВ, АМОРУМ, АПЛ, АСЧ, ДДОБ, ПУО и некоторые другие. Принципы расчета амортизации имущества, заложенные в этих функциях, аналогичны. Различие состоит лишь в использовании различных систем бухгалтерского учета (например, функции АМОРУМ и АМОРУВ основаны на французской системе) и различных методов оценки амортизации: линейного, «суммы (годовых) чисел», двойного уменьшения остатка и т.п.

В наиболее часто используемых функциях расчета амортизации имущества. обычно используются следующие аргументы (см. табл.4.2):

Таблица 4.2 - Аргументы функций расчета амортизации

Нач_стоим	Начальная стоимость имущества
Ост_стоимость	Остаточная (ликвидационная стоимость имущества)
Время_эксплуат	Период амортизации
Период	Период для начисления амортизации

Все аргументы в функциях должны изменяться в одинаковых периодах - в годах или месяцах.

- Функция АПЛ(нач_стоим; ост_стоим; время_эксплуатации) – вычисляет величину непосредственной амортизации имущества за один период, рассчитанную линейным методом. Предполагается, что стоимость имущества уменьшается равномерно в течение всего времени эксплуатации.

- Функция АСЧ(нач_стоим; ост_стоим; время_эксплуатации; период) - возвращает величину амортизации актива за данный период, рассчитанную методом «суммы (годовых) чисел».

- Функция ДОБ(нач_стоим; ост_стоим; время_экспл; период; коэффициент) - вычисляет амортизацию имущества на основе метода двукратного учета амортизации. Коэффициент - это норма снижения балансовой стоимости - является необязательным аргументом и по умолчанию принимается равным 2, при этом используется метод двукратного учета амортизации.

ПРАКТИЧЕСКАЯ ЧАСТЬ

Пример 4.1

Предположим, имеется инвестиционный проект, в который требуется вложить 24 млн. руб., а доход, получаемый от реализации проекта, составляет 6 млн. руб. в течение 5 лет. Требуется оценить выгодность проекта при банковской ставке 4,5% годовых.

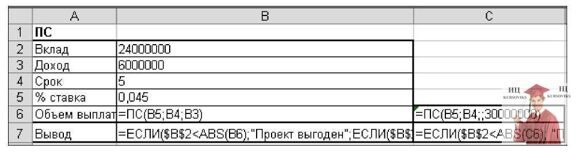
Разместим данные в ячейках рабочего листа Excel, как показано на рисунке 4.1, и воспользуемся функцией ПС (см. рис. 4.2): =ПС(4,5%; 5; 6000000) или в терминах ячеек рабочего листа Excel: =ПС(B5;B4;B3).

В результате вычислений по этой формуле Excel выдаст результат -26339860,47. То есть при этой процентной ставке сумма в 26339860,47 руб. принесет в течение пяти лет доход 30 млн. руб. Так как требуемый вклад составляет всего 24 млн. руб., то инвестиция будет выгодной. Для вывода комментария о выгодности проекта в ячейку В 7 внесена формула

=ЕСЛИ($B$2 < ABS(B6); "Проект выгоден"; ЕСЛИ ($B$2 = ABS(B6); "Граничная точка выгодности"; "Проект не выгоден"))

Рис. 4.1 - Анализ инвестиций. Результаты расчета

Рис. 4.2 - Анализ инвестиций. Формулы

Пример 4.2

Требуется проанализировать инвестиционный проект со следующими характеристиками: предварительный вклад 175 млн. руб.; ожидаемые доходы по годам 30 млн. руб., 70 млн. руб., 70 млн. руб., 45 млн. руб.; цена капитала 12%.

Разместим исходные данные в ячейках А11:В16 рабочей книги ЭТ Excel и используем функцию ЧПС: ЧПС(12%;30000000;70000000;70000000;45000000) - 175000000.

Или в терминах ячеек рабочего листа Excel (см. рисунки 4.7 и 4.8): =ЧПС(B16;B12:B15)-B11

Рис. 4.7 - Анализ инвестиционного проекта. Расчеты

Рис. 4.8 - Анализ инвестиционного проекта. Формулы

Полученный результат -13987783,41 руб. свидетельствует о том, что данный проект невыгоден. Отрицательное значение формулы означает, что реальная стоимость проекта ниже запрашиваемой на 13987783,41 руб.

Пример 4.3

Предположим, что известен размер вклада, который будет помещен на определенный срок под заданный процент. Требуется вычислить коэффициент наращивания (т.е. значение, показывающее, во сколько раз вырастет вклад за указанный срок) и сумму выплат в конце периода.

Разместим исходные данные в ячейках А22:С25 рабочего листа Excel (см. рис.4.9). В ячейках В29 и С29 выполним расчеты будущего значения вклада для вклада размером 1500000 руб. и для вклада размером 2000000 руб. с помощью функции БС. Составим ее.

Для вклада в 1500000 руб.:

- без постоянных периодических выплат: =БС(5%; 10; 0; -1500000);

- с постоянными периодическими выплатами (взносами) в размере 500000 руб. ежегодно: =БС(5%; 10; -500000; -1500000).

Для вклада в 2000000 руб.:

- без постоянных периодических выплат: =БС (10 %; 3; 0; -2000000);

- с постоянными периодическими выплатами (взносами) в размере 500000 руб. ежегодно: =БС(10%; 3; -1000000; -2000000).

На рисунке 4.9 приведены результаты расчетов и показана формула (ячейка В29) для вычисления будущего значения вклада для вклада размером 1500000 руб.

В формулах БС значение последнего аргумента тип опущено. Это значит, что выплаты (в рассматриваемом расчете взносы) осуществлялись в конце каждого года. Если задать этот аргумент равным 1, то есть производить выплаты (взносы) в начале каждого года, то результат будет больше.

Рис. 4.9 - Расчет будущего значения вклада

 

Пример 4.4

Пусть взят кредит на строительство жилья в сумме 15 млн. руб. на 6 лет под годовую банковскую ставку 14%. Требуется рассчитать ежемесячные выплаты для возврата долга.

- Поместим исходные данные для расчета в ячейки А44: В46 рабочего листа Excel (см. рис. 4.10) и рассчитаем сумму общего ежемесячного платежа, для чего составим функцию ПЛТ

ПЛТ(14%/12; 6*12; 15000000) и получим результат -309086,09. Отрицательное значение получается потому, что деньги надо отдать.

- Рассчитаем выплаты по процентам за первый месяц, второй месяц и последний месяц шестилетнего периода. Для этого составим формулы с использованием функции ПРПЛТ.

Выплата по процентам за первый месяц периода:

ПРПЛТ (14%/12; 1; 6*12; 15000000) результат -175000 руб.

Выплата по процентам за последний месяц периода

ПРПЛТ(14%/12; 6*12; 6*12; 15000000) результат -35 64,4 2руб.

- Рассчитаем величину основного платежа за первый месяц, второй месяц и последний месяц шестилетнего периода. Для этого составим формулы с использованием функции ОСПЛТ.

Основная выплата за первый месяц периода:

ОСПЛТ (14%/12;1; 6*12; 15000000) результат -134086,09 руб.

Основная выплата за последний месяц периода:

ОСПЛТ(14%/12; 6*12; 6*12; 15000000) результат -305521,6 руб.

На рисунке 4.11 представлены формулы в терминах ячеек рабочего листа Excel. Нетрудно убедиться, что сумма выплаты по процентам и основные выплаты за полный период равны полной величине выплаты, вычисляемой с помощью функции ПЛТ.

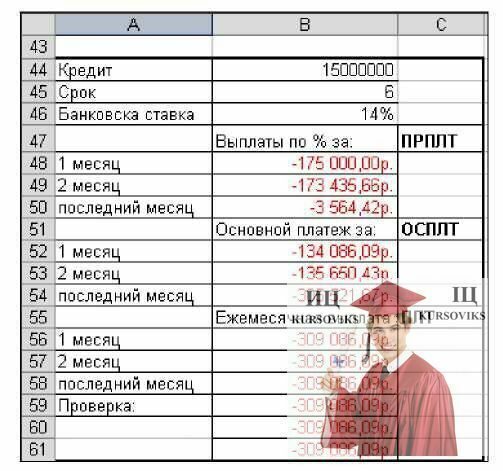
Рис. 4.10 - Расчет выплат по кредиту. Результаты

Рис. 4.11 - Расчет выплат по кредиту. Формулы

 

Пример 4.5

Определить амортизацию поточной линии стоимостью 35 млн. руб., срок эксплуатации которой 6 лет, после чего ее стоимость оценивается в 15 млн. руб. Предположить равномерное уменьшение стоимости имущества.

Разместим исходные данные в ячейках А2: В4 рабочего листа Excel (см. рис. 4.12) и в ячейке В5 составим функцию АПЛ:

=АПЛ(35000000; 15000000;6) или =АПЛ(B2; B4; B3)) для исходных данных в ячейках В2:В4.

Рис. 4.12 - Расчет амортизации с использованием функции АПЛ

Таким образом, функция АПЛ вернет результат 3,33 млн.руб. – непосредственную амортизацию за каждый год эксплуатации.

 

Пример 4.6

Обратимся к условию примера 4.5 и рассчитаем амортизацию поточной линии стоимостью 35 млн. руб., срок эксплуатации которой 6 лет, после чего ее стоимость оценивается в 15 млн. руб., используя метод «суммы (годовых) чисел».

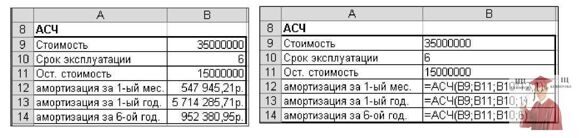
Разместим исходные данные в ячейках А9:В14 рабочего листа Excel (см. рис. 4.13) и составим функцию АСЧ:

- для вычисления амортизации за первый месяц эксплуатации (ячейка В12):

=АСЧ(350 00000; 15000000; 6*12; 1) или в терминах ячеек рабочего листа Excel:

=АСЧ (В2; В4; В3*12; 1);

- для вычисления амортизации за первый год эксплуатации (ячейка В13):

= АСЧ(35000000; 15000000;6;1) или в терминах ячеек рабочего листа Excel: = АСЧ (В2; В4; В3; 1).

Таким образом, функция АСЧ вернет значения амортизации поточной линии в сумме 547945,21 руб. - амортизацию за первый месяц эксплуатации, 5714285,71 руб.- амортизацию за первый год эксплуатации и 952380, 95 руб. - амортизацию за последний год эксплуатации (см. рис. 4.13).

Рис. 4.13 - Расчет амортизации с использованием функции АСЧ

 

Пример 4.7

Обратимся к условию примера 4.5 и рассчитаем амортизацию поточной линии стоимостью 35 млн. руб., срок эксплуатации которой 6 лет, после чего ее стоимость оценивается в 15 млн. руб., используя метод удвоенного процента со снижающегося остатка.

Разместим исходные данные в ячейках D2:E7 рабочего листа Excel (см. рис. 4.14) и составим функцию ДДОБ:

- для вычисления амортизации за первый месяц эксплуатации (ячейка E5):

= ДДОБ(35000000; 15000000; 6*12; 1) или в терминах ячеек рабочего листа Excel:

=ДДОБ(E2; E4; E3*12; 1);

- для вычисления амортизации за первый год эксплуатации (ячейка E 6):

=ДДОБ(35000000; 15000000; 6; 1) или в терминах ячеек рабочего листа Excel:

=ДДОБ(E2; E4; E3; 1).

Таким образом, функция ДДОБ вернет значение 972222,22 руб. -двукратную амортизацию за первый месяц, значение 11666666, 67 руб. -двукратную амортизацию за первый год и значение 555555,56 руб. -двукратную амортизацию за третий год (см. рис. 4.17).

Рис. 4.17 - Расчет амортизации с использованием функции ДДОБ

 

Задания для самостоятельной работы

Заказать можно здесь!

Задание 1. Для ОАО «Екатеринбургский мясокомбинат» приобретено следующее оборудование.

Наименова ние оборудова ния	Количе ство единиц, шт.	Стоимость единицы оборудования, тыс. руб.	Стои мость всех машин, руб.	Наклад ные расходы, руб.	Стои мость итого, руб.	Остаточная стоимость, руб.	Время эксплуа тации	Сумма амортиза ции	Средняя норма амортизации
Поточная линия	2	199560				230000	6
Произ водственные станки	9	88200				500000	6
Транспорт ные средства	1					1000000	6
Мебель	1	15200				5100	6
Оргтехника	1	8300				4000	5
Компьютеры	6	2100				9500	3
Освети тельные приборы	12	175				500	6
Холоди льники	2	1300				1100	6
Микровол новая печь	2	370				400	5
Обогре ватели	8	180				700	5
Автомобиль	1	35400				15700	15
Грузовик	1	52100				24500	6
Здание	1	165800				1100000	10

Приняв накладные расходы равными 12% от общей стоимости, рассчитать сумму амортизации и среднюю норму амортизации.

Средняя норма амортизации = Сумма амортизации/Стоимость итого* 100.

Использовать финансовые функции АПЛ, АСЧ, ДДОБ.

Составить простейшие отчетные ведомости, на которых графически отразить результаты расчетов.

Задание 2. Инвесторам со свободными капиталами (см. таблица 4.4) предлагаются независимые проекты (см. таблица 4.5):

Таблица 4.4 – Свободные капиталы

Таблица 4.5 - Варианты инвестиционных проектов

№ проекта	Инвестиции I0, млн.руб.	Годовые поступления, млн.руб.
		1	2	3	4	5	6
1	-100	10	20	40	40	40	10
2	-100	-10	40	40	30	20	10
3	-200	100	100	100	100	100
4	-200	-80	100	100	80	70	70
5	-250	50	100	100	100	70
6	-300	280	120	100
7	-400	200	200	200	200
8	-500	100	200	200	200	100
9	-600	300	200	200	200	100	50
10	-550	100	200	250	200	100

Годовая банковская ставка 15%. Произвести сравнительный анализ инвестиционных проектов и определить оптимальную комбинацию для каждого инвестора. Оценку проекта выполнить по трем критериям:

- чистой приведенной стоимости NPV(использовать функцию ЧПС),

- внутренней норме прибыли IRR (использовать функцию ВСД),

- показателю рентабельности PI = NPV/ I₀ (Проект рентабелен, если PI ≥ 1,2).

Если показатель рентабельности проекта окажется ниже нормы (PI ≤ 1,2) подобрать такое значение банковской ставки, при котором инвестиции будут рентабельны (использовать команду Подбор параметра).

С уважением ИЦ "KURSOVIKS"!