Методичні вказівки до лабораторної роботи №3 на тему Якісний аналіз двовимірних лінійних динамічних систем, Дослідження системи на наявність станів рівноваги, їх типу та стійкості
|
« Назад 1. Запишіть систему рівнянь у розгорнутому вигляді (згадайте множення матриць). 2. Надрукуйте систему у цьому пункті, відповідно до варіанту а) – в). Класифікація стаціонарних точок. Розглянемо спочатку найпростішу систему рівнянь де aij – сталі числа. Очевидно, що якщо a11a22, - a12a21 ≠0, то (3) має лише одну стаціонарну точку х1* = х2* = 0 і це є розв’язок (3) при нульових початкових умовах. Нетривіальний розв’язок шукаємо у вигляді де С, D – сталі. Тоді з (3) матимемо систему лінійних однорідних рівнянь Вона має розв’язок в випадку, коли 5. Для кожної системи складіть характеристичне рівняння, запишіть у цьому пункті і знайдіть його розв’язки λ1 та λ2. Запишіть їх у цьому пункті. 6. Проведіть дослідження розв’язків (коренів) λ1 та λ2.характеристичного рівняння. Надрукуйте у цьому пункті висновки. Можна виділити такі випадки:
І. Корені (2)
Проаналізуємо наступні варіанти знаків
1. Якщо
і незалежно від початкових умов ми з часом попадем в точку х1 = х2 = 0. Такий тип стаціонарної точки називається стійким вузлом. Траєкторії на фазовій площині поблизу стійкого вузла показано на рис. 1.
2. Якщо
Такий тип стаціонарної точки називається нестійким вузлом, з часом ми віддаляємося від неї. Поведінку траєкторій а фазовій площині показано на рис. 2.
Рис. 1 - Стійкий вузол
Рис. 2 - Нестійкий вузол
3. Якщо
Така стаціонарна точка також нестійка і називається сідлом. Поведінка траєкторій на фазовій площині показана на рис. 3.
Рис. 3 - Сідло
ІІ. Корені (2)
В залежності від знаку p можливі такі типи стаціонарних точок:
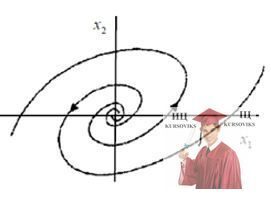
4. p ˂ 0, стаціонарна точка х1 = х2 = 0 називається стійким фокусом. Поведінку траєкторії на фазовій площині поблизу стійкого фокуса показна на рис.4.
5. p ˃ 0, стаціонарна точка х1 = х2 = 0 називається нестійким фокусом. Поведінку траєкторії на фазовій площині поблизу стійкого фокуса показна на рис.5.
Рис. 4 - Стійкий фокус
Рис. 5 - Нестійкий фокус
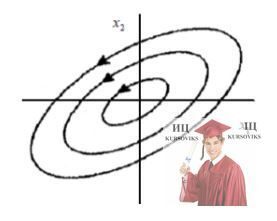
6. p = 0. Траєкторія – замкнута крива, еліпс, з центром в точці (0,0). Така стаціонарна точка називається центром (рис. 6).
Рис. 6 - Центр
7. Застосуйте інший метод дослідження стаціонарних точок, виконайте необхідні обчислення і заповніть таблицю.
Метод визначення стаціонарної точки. Для визначення типу стаціонарної точки системи диференціальних рівнянь (1) не обов’язково обчислювати
слід та визначник матриці А. Тоді характеристичне рівняння запишеться у вигляді
Розглянемо площину з прямокутними координатами (Tr, Δ) і позначимо на ній області, що відповідають тому чи іншому характеру особливої точки (рис. 7).
Необхідні і достатні умови стійкості стаціонарної точки мають вигляд
Tr ˂ 0, Δ ˃ 0.
На рис.7 цим умовам відповідають точки, розташовані в другій чверті. Стаціонарна точка буде фокусом, якщо виконана умова Tr2 - 4Δ ˂ 0, і цій умові відповідають точки, що розташовані в середині параболи Tr2 = 4Δ. Якщо Δ ˂ 0, то стаціонарна точка буде сідлом. На напівпрямій Tr = 0, Δ ˃ 0 знаходяться центри. Парабола Tr2 = 4Δ – це лінія рівних коренів
Завдання 2. Побудуйте фазовий портрет. З повагою ІЦ "KURSOVIKS"! |
||||||||||||||||||||||||||||||||||||||||||||||||||
















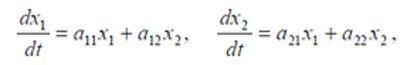

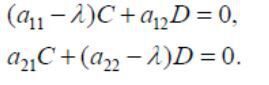
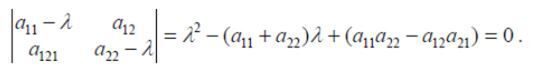
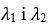 – дійсні і різні.
– дійсні і різні. , то
, то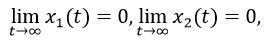



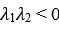 , то
, то

 .
.
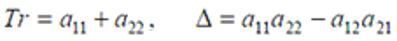

 , або, як неважко переконатися,
, або, як неважко переконатися,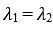 , і вона відділяє фокуси від вузлів. Пряма Δ = 0 відділяє вузли від сідел.
, і вона відділяє фокуси від вузлів. Пряма Δ = 0 відділяє вузли від сідел.